
第一章 涵数与极限 函数一 研究对象 分析基础 极限 一研究方法 连续一1 研究桥梁
第一章 分析基础 函数 极限 连续 — 研究对象 — 研究方法 — 研究桥梁 函数与极限

第一节 第一章 映射与函数 集合 二、 映射 三、函数 O9o⊙o8
第一章 二、映射 三、函数 一、集合 第一节 机动 目录 上页 下页 返回 结束 映射与函数

一、集合 1.定义及表示法 定义1.具有某种特定性质的事物的总体称为集合 组成集合的事物称为元素 不含任何元素的集合称为空集,记作☑. 元素a属于集合M,记作a∈M 元素a不属于集合M,记作a∈M(或a廷M), M表示M中排除0的集; 注:M为数集 M+表示M中排除0与负数的集 OOo⊙08
元素 a 属于集合 M , 记作 元素 a 不属于集合 M , 记作 一、 集合 1. 定义及表示法 定义 1. 具有某种特定性质的事物的总体称为集合. 组成集合的事物称为元素. 不含任何元素的集合称为空集 , 记作 . a M ( 或 aM ) . a M . 注: M 为数集 * M 表示 M 中排除 0 的集 ; + M 表示 M 中排除 0 与负数的集 . 机动 目录 上页 下页 返回 结束

表示法: (1)列举法:按某种方式列出集合中的全体元素 :有限集合A={a1,a2,an}={a,}” 自然数集N={0,1,2,.,n,.}={n} (2)描述法:M={xx所具有的特征} 例:整数集合Z={xx∈N或-xeN+} 有理数关0-{品pe乙geN,与g互质} 实数集合 R={xx为有理数或无理数} 开区间(a,b)={xa<x<b} 闭区间[a,b]={xa≤x≤b
表示法: (1) 列举法:按某种方式列出集合中的全体元素 . 例: 有限集合 A = a1 , a2 , , an n i i a =1 = 自然数集 N = 0, 1, 2 , , n, = n (2) 描述法: M = x x 所具有的特征 例: 整数集合 Z = x x N 或 + − x N 有理数集 q p Q = Z, N , + p q p 与 q 互质 实数集合 R = x x 为有理数或无理数 开区间 ( a , b ) = x a x b 闭区间 [ a , b ] = x a x b 机动 目录 上页 下页 返回 结束

半开区间[a,b)={xa≤x<b} (a,b]={xa<x≤b} 无限区间[a,+o)={xa≤x} (-0,b]={xx≤b} (-,+)=ix1R afo a ato 点的6邻域U(a,6)={xa-6<x<a+6} ={xx-a<8} 去心6邻域U(a,6)={x0<x-a<8} 其中,α称为邻域中心,6称为邻域半径 左6邻域:(a-6,a),右6邻域:(a,a+) Oao⊙⊙8 机无
( ) a − a + 无限区间 点的 邻域 a 其中, a 称为邻域中心 , 称为邻域半径 . 半开区间 去心 邻域 左 邻域 : 右 邻域 : 机动 目录 上页 下页 返回 结束

2.集合之间的关系及运算 定义2.设有集合A,B,若x∈A必有x∈B,则称A 是B的子集,或称B包含A,记作AB. 若AcB且BCA,则称A与B相等,记作A=B. 例如,NCZ,ZCQ,QCR 显然有下列关系: (1)ACA;A=A4;CA (2)ACB且BcC>ACC Oao⊙⊙8
是 B 的子集 , 或称 B 包含 A , 2. 集合之间的关系及运算 定义2 . 则称 A A B. 若 且 则称 A 与 B 相等, A = B . 例如 , 显然有下列关系 : , , 设有集合 A,B, 若 x A x B, 记作 记作 必有 机动 目录 上页 下页 返回 结束

定义3.给定两个集合A,B,定义下列运算 并集AUB={xx∈A或x∈B} AUB 交集A∩B={xx∈A且x∈B} AB 差集A八B={xx∈A且xEB} A∩B 余集B=A\B(其中BCA) 直积A×B={(x,y)x∈A,y∈B} 特例: RXR记R2 B AxB 为平面上的全体点集 OOo⊙⊙8
A c BA B 定义 3 . 给定两个集合 A, B, 并集 A B = x 交集 A B = x 且 差集 A \ B = x 且 x B 定义下列运算: A B A B 余集 B A\ B ( B A) c A = 其中 直积 A B = (x, y) x A , y B 特例: RR 记 2 R 为平面上的全体点集 A A\ B B A B A B 机动 目录 上页 下页 返回 结束 或
二、 映射 1.映射的概念 引例1. 某校学生的集合 学号的集合 按一定规则查号 某教室座位 某班学生的集合 的集合 按一定规则入座 oo0oo
二、 映射 1. 映射的概念 某校学生的集合 学号的集合 按一定规则查号 某班学生的集合 某教室座位 的集合 按一定规则入座 机动 目录 上页 下页 返回 结束 引例1
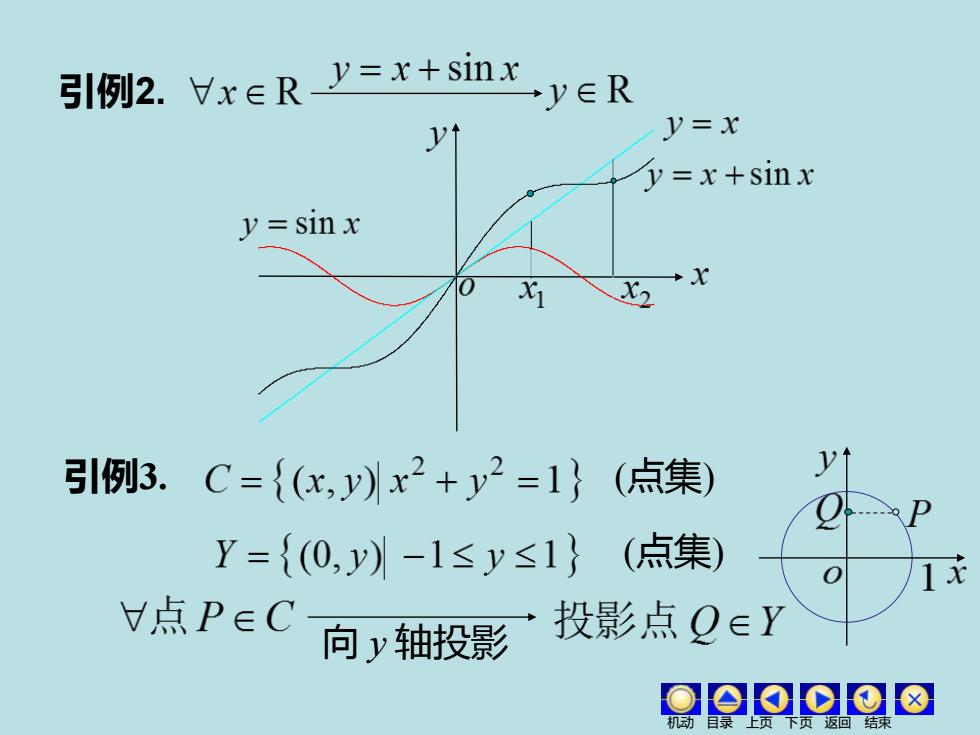
引例2.Vx∈Ry=x+sinxy∈R y=x V=x+sinx y=sin x x 引例3.C={(x,y)x2+y2=1}(点集) Y={(0,y)-1≤y≤1}(点集) V点PeC 向y轴投影 投影点QeY o0o0 机
引例2. 引例3. (点集) (点集) 向 y 轴投影 机动 目录 上页 下页 返回 结束

定义4.设X,Y是两个非空集合,若存在一个对应规 则f,使得Vx∈X,有唯一确定的yeY与之对应,则 称f为从X到Y的映射,记作f:X→Y. 元素y称为元素x在映射f下的像,记作y=f(x) 元素x称为元素y在映射f下的原像. 集合X称为映射f的定义域; Y的子集f(X)={f(x)x∈X}称为f的值域 注意:1)映射的三要素一定义域,对应规侧,值域 2)元素x的像y是唯一的,但y的原像不一定唯一 gao⊙回⑧
定义4. 设 X , Y 是两个非空集合, 若存在一个对应规 则 f , 使得 有唯一确定的 与之对应 , 则 称 f 为从 X 到 Y 的映射, 记作 f : X →Y. 元素 y 称为元素 x 在映射 f 下的 像 , 记作 y = f (x). 元素 x 称为元素 y 在映射 f 下的 原像 . 集合 X 称为映射 f 的定义域 ; Y 的子集 f (X) = f (x) x X 称为 f 的 值域 . 注意: 1) 映射的三要素— 定义域 , 对应规则 , 值域 . 2) 元素 x 的像 y 是唯一的, 但 y 的原像不一定唯一 . X f Y 机动 目录 上页 下页 返回 结束