
第三为 第一章 西教的极限 对y=f(x),自变量变化过程的六种形式: (1)x→x0 (4)x→0 (2)x→x0 (5) X→十00 (3)x→0 (6) X→-00 本节内容: 一、自变量趋于有限值时函数的极限 二、自变量趋于无穷大时函数的极限 OOo⊙08 机
第一章 一、自变量趋于有限值时函数的极限 第三节 自变量变化过程的六种形式: 二、自变量趋于无穷大时函数的极限 本节内容 : 机动 目录 上页 下页 返回 结束 函数的极限

一、自变量趋于有限值时函数的极限 1.x→xo时函数极限的定义 引例.测量正方形面积(真值:边长为x。;面积为A) 直接观测值 确定直接观测值精度6: 边长x x-x0<δ 间接观测值 任给精度c,要求x2-A<G 面积x2 A Xo Qao⊙⊙8
一、自变量趋于有限值时函数的极限 1. 时函数极限的定义 引例. 测量正方形面积. (真值: 边长为 面积为A ) 边长 面积 直接观测值 间接观测值 任给精度 , 要求 x − A 2 确定直接观测值精度 : x − x0 0 A x 机动 目录 上页 下页 返回 结束

定义1.设函数f(x)在点x0的某去心邻域内有定义, 若Vε>0,6>0,当00,36>0,当x∈U(xo,6) x→X0 时,有f(x)-A<6 几何解释: ↑y 这表明: 4+ 业三f(x) A 极限存在 A-8 函数局部有界 (P36定理2) x0-8X0x0+δx OOo⊙08 机元
定义1 . 设函数 在点 的某去心邻域内有定义 , 0, 0, 当 0 x − x0 时, 有 f (x) − A 则称常数 A 为函数 当 时的极限, f x A x x = → lim ( ) 0 或 即 当 时, 有 若 记作 几何解释: x0 + A+ A− A x0 x y y = f (x) 极限存在 函数局部有界 (P36定理2) 这表明: 机动 目录 上页 下页 返回 结束

例1.证明limC=C(C为常数) X→xo 证: f(x)-A=C-C=0 故H6>0,对任意的6>0,当0<x-x<6时, 总有 C-C=0<8 因此 lim C=C x→x0 OO▣⊙⊙☒
例1. 证明 证: f (x) − A 故 0, 对任意的 0, 当 时 , 因此 总有 机动 目录 上页 下页 返回 结束

例2.证明1im(2x-1)=1 X→ 证: f(x)-A=(2x-1)-1=2x-1 Vε>0,欲使 fx)-4<6,只要x-1<3, 取8=,则当0<x-1<8时,必有 f(x)-A=(2x-1)-1<8 因此 lim(2x-1)=1 OOo⊙o8 机无
例2. 证明 证: = 2 x −1 0, 欲使 取 , 2 = 则当 0 x −1 时 , 必有 因此 只要 机动 目录 上页 下页 返回 结束

2-1 例3.证明1im 2 x1x-1 证:f)-A= =x+1-2=x-1 故Vε>0,取6=8,当0<x-1<6时,必有 x2-1-2<6 x-1 x2-1 因此 lin x→1X-1 Oao⊙⊙8
例3. 证明 证: f (x) − A 故 0, 取 = , 当 时 , 必有 − − − 2 1 1 2 x x 因此 2 1 1 lim 2 1 = − − → x x x 机动 目录 上页 下页 返回 结束

例4.证明:当xo>0时1im√x=√xo: x→X0 证:/0-4=Vx-√0= x-xo x+2 Ve>0,欲使fx)-A<6,只要x-<x6,且 x≥0.而x≥0可用x-xo≤x保证.故取 6=min{√xe,x},则当0<x-xo<6时,必有 x-√<8 因此 lim√x=√xo x Xo x→X0 Ooo⊙®8
例4. 证明: 当 证: 0 0 1 x x x − 0, 欲使 且 而 可用 因此 只要 0 0 lim x x x x = → 时 故取 min , , 0 0 = x x 则当 0 x − x0 时, 保证 . 必有 o x x0 x 机动 目录 上页 下页 返回 结束
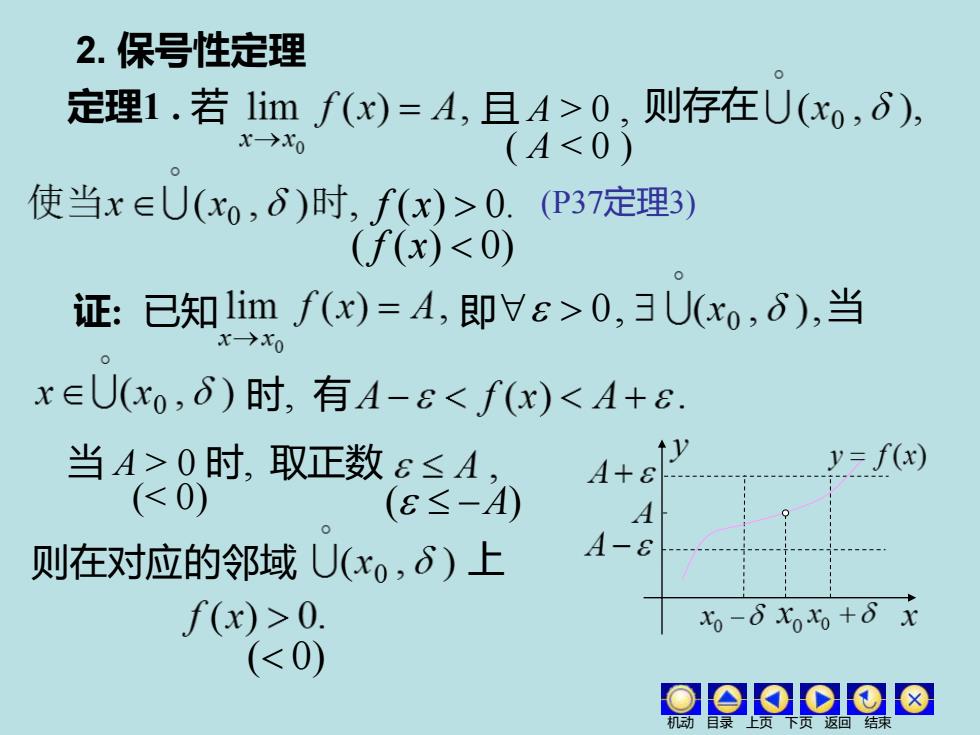
2.保号性定理 定理1.若1imf(x)=A,且A>0,则存在U(xo,6), x→x0 (A0.(P37定理3) (f(x)0,3U(xo,6),当 x∈U(xo,6)时,有A-&0时,取正数6≤A, ↑y A+ y=f(x) (0. x-δX0+6x (<0)
2. 保号性定理 定理1 . 若 且 A > 0 , f (x) 0. ( f (x) 0) 证: 已知 即 0, 当 时, 有 当 A > 0 时, 取正数 则在对应的邻域 上 (< 0) ( −A) 则存在 ( A < 0 ) (P37定理3) ( 0) 机动 目录 上页 下页 返回 结束

推论:若1imf(x)=A≠0,则存在U(xo,6),使当 x→X0 xeU,ò)时有1f)>. (P37推论) 分析: A-&0: A+ A A-8 A<0:-34 <f)<-4 -6X0x+6x OO▣⊙⊙8
A 0: A 0: 若取 , 2 A = 则在对应的邻域 上 若 则存在 使当 时, 有 推论: 2 3 ( ) 2 A f x A 2 ( ) 2 3 A f x A − − (P37 推论) 分析: 机动 目录 上页 下页 返回 结束

定理2.若在x,的某去心邻域内f(x)≥0,且 (f(x)≤0) imf(x)=A,则A≥0. x→X0 (A≤0) 证:用反证法.当f(x)≥0时,假设A0,是否必有A>0? 不能!如immx2=0 x→0
定理 2 . 若在 的某去心邻域内 f (x) 0 ( f (x) 0) , 且 则 A 0. (A 0) 证: 用反证法. 则由定理 1, 的某去心邻域 , 使在该邻域内 与已知 所以假设不真, A 0 . (同样可证 f (x) 0 的情形) 思考: 若定理 2 中的条件改为 f (x) 0, 是否必有 A 0? 不能! 存在 如 假设 A < 0 , 条件矛盾, 故 机动 目录 上页 下页 返回 结束