
呼和浩特职业学院 2008~2009学年第一学期高等数学试卷(B) 注意事项:1、本试卷共6页,满分100分,考试时间为120分钟。 2、答题时请使用蓝、黑钢笔或圆珠笔。 3、考试形式:闭卷(开、闭) 项目 二 四 五 六 七总分 得分 得分评卷人 一、洗择颗:(20) 1、已知f(x)的定义域为[0,1],则fx2)的定义域为( A.[0,1] B.[-1,0]C.[-1,1]D.不能确定 32、函数f(x)=m(x+V1+x2)是( 呼 A、偶函数:B、奇函数: C、非奇非偶函数:D、既是奇又是偶函数 1-x 笔3设fx)=+8=1,则当x→1时(力 A、f(x)是比g(x)高阶的无穷小 B、f(x)是比g(x)低阶的无穷小 C、fx)与g(x)为同阶无穷小 D、f(x)与g(x)为等价无穷小 A.ef(e") B.e"/(e")+e"f(e") C.e"f(e') D.e"f'(e*)+e*f(e*) 5、下列关系式正确的是( A、dfx)t=fx) B、∫f(x)dk=fx) c、 乐ra国 D乐=+C 第1页共6页
第 1 页 共 6 页 呼和浩特职业学院 2008 ~2009 学年第一学期高等数学 试卷(B) 注意事项:1、本试卷共 6 页,满分 100 分,考试时间为 120 分钟。 2、答题时请使用蓝、黑钢笔或圆珠笔。 3、考试形式: 闭 卷(开、闭) 项 目 一 二 三 四 五 六 七 总分 得 分 得分 评卷人 一、选择题:(20’) 1、已知 f (x) 的定义域为[0,1],则 ( ) 2 f x 的定义域为( ) A.[0,1] B.[-1,0] C.[-1,1] D.不能确定 2、函数 ( ) ln( 1 ) 2 f x = x + + x 是( ) A、偶函数; B、奇函数; C、非奇非偶函数;D、既是奇又是偶函数 3、设 2(1 ) 1 ( ) x x f x + − = , g(x) = 1− x ,则当 x →1 时( )。 A、 f (x) 是比 g(x) 高阶的无穷小 B、 f (x) 是比 g(x) 低阶的无穷小 C、 f (x) 与 g(x) 为同阶无穷小 D、 f (x) 与 g(x) 为等价无穷小 4、设函数 ( ) x y = f e ,则 = 2 2 dx d y ( ) A. ( ) 2x " x e f e B. ( ) ( ) 2x " x x ' x e f e + e f e C. ( ) x " x e f e D. ( ) ( ) x " x x ' x e f e + e f e 5、下列关系式正确的是( ) A、 d f (x)dx = f (x) B、 ( ) ( ) ' f x dx = f x C、 f (x)dx f (x) dx d = D、 f x dx f x C dx d = + ( ) ( ) .装.订.线. 班级 学号 姓名 密 封 线 内 不 要 答 题

6、下列广义积分收敛的是( ) 「2+122] 7、当1=( )时, 111的秩为2。 112 A、0 B、1 C、2 D、3 区以下矩库中,与矩库0】案法可换的矩陈为了 )。 cb g 9、从装有a只黑球,b只白球的袋中,采用有放回的摸球,以A表示第一次摸到黑球,B表示第 二次摸到黑球的事件,则P(AB)=( )。 A.atb B、a+b C.(+b D.(a+b) 10、设5服从参数1=)的指数分布,则P3<5<9}=() A∫eh 得分评卷人 二、填空题:(17》 1、函数y=arcsin-华的定义域为 2、设m0-m片=e2,则m= 3、设fx)=xx+1(x+2(xn求∫(0)= 4、已知y=kan2x的一个原函数为号hc0s2x,则k- 第2项共6页
第 2 页 共 6 页 6、下列广义积分收敛的是( ) A、 + 1 1 dx x B、 + 0 + 2 1 dx x x C、 + 1 ln dx x x D、 + 1 3 1 dx x 7、当 =( )时, + 1 1 2 1 1 1 1 2 2 的秩为 2。 A、0 B、1 C、2 D、3 8、以下矩阵中,与矩阵 0 1 1 1 乘法可换的矩阵为( )。 A、 0 2 0 1 B、 1 1 1 1 C、 0 2 2 3 D、 − − 2 1 1 1 9、从装有 a 只黑球, b 只白球的袋中,采用有放回的摸球,以 A 表示第一次摸到黑球, B 表示第 二次摸到黑球的事件,则 P(AB) = ( )。 A、 a b a + B、 a b b + C、 2 2 (a b) a + D、 2 2 (a b) b + 10、设 服从参数 9 1 = 的指数分布,则 P{3 9} = ( ) A、 dx x 9 3 9 e B、 ) 1 1 ( 9 1 3 e e − C、 e e 1 1 3 − D、 dx x 9 − 3 9 e 二、填空题:(17’) 1、函数 5 3 2 arcsin x y − = 的定义域为_。 2、设 ( ) 2 1 0 lim 1 mx x e x − = → ,则 m=_。 3、设 f(x)=x(x+1)(x+2).(x+n),求 (0) ' f =_。 4、已知 y = k tan 2x 的一个原函数为 ln cos 2x 3 2 ,则 k =_。 得分 评卷人

5、5m2xd= 「-122] 6、设A=-120,则34= 011 号012 8设5的分布列为P,则E氏=一D=一 E(32+4)= 288 得分评卷人 三、计算题:(35) 2me-) 3人设y=g产-0+)an,求y0.小n恤 5、求由方程xy+(y-x)=x所确定的函数的导数。 第3页共6页
第 3 页 共 6 页 5、 = xdx 2 0 2 sin 。 6、设 − − = 0 1 1 1 2 0 1 2 2 A ,则 3A =_。 7、设 A, B 为相互独立的随机事件,且已知 , 10 7 , ( ) 10 6 P(A) = P A + B = 则 P(B) = _。 8、设 的分布列为 8 1 8 3 2 1 P 0 1 2 ,则 E= , D= , E(3 +4)= 2 。 三、计算题:(35’) 1、 − − → 1 1 1 lim 0 x x x e 2、 lim ( 1) 1 − → x x x e 3、设 x x e x y x 3(1 ) arctan cos 2 = − + ,求 (0) ' y 。 4、 1 ln e e x dx 5、求由方程 xy + ln( y − x) = x 所确定的函数的导数。 得分 评卷人

6%高 入求微分方程会-ym=的道解。 得分评卷人四、设某厂生产某种商品的固定成本为200(百元),每生产一个单位商品, 成本增加5(百元),且己知需求函数Q=100-2p(其中p为价格,Q为产量), (1)求该商品的总成本函数C(p以边际成本函数和总收益函数Rp以、边际收 益函数:(2)求出使该商品的总利润最大的产量:(3)求最大利润。(6) 第4页共6页
第 4 页 共 6 页 6、 − − 1 4 3 1 x 1 dx 7、求微分方程 y x x dx dy − tan = sec 的通解。 四、设某厂生产某种商品的固定成本为 200(百元),每生产一个单位商品, 成本增加 5(百元),且已知需求函数 Q=100-2p(其中 p 为价格,Q 为产量), (1)求该商品的总成本函数 C(p)、边际成本函数和总收益函数 R(p)、边际收 益函数;(2)求出使该商品的总利润最大的产量;(3)求最大利润。(6’) 得分 评卷人
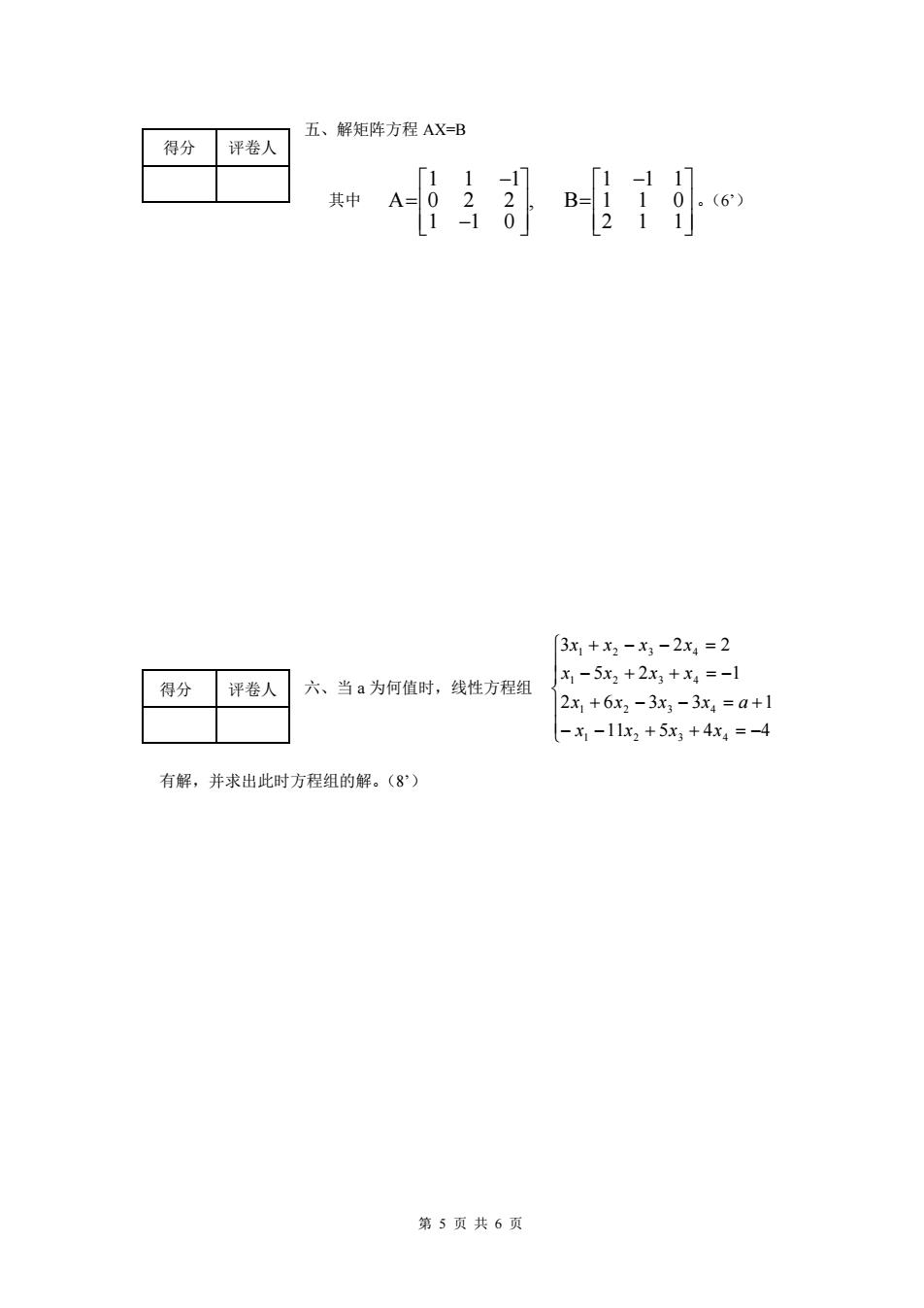
得分评卷人 五、 解矩阵方程AX=B 其中 [3x+x2-x3-2x4=2 得分评卷人 六、当a为何值时,线性方程组 x1-5x2+2x3+x4=-1 2x1+6x3-3x3-3x=a+1 -11x2+5x3+4x,=-4 有解,并求出此时方程组的解。(8) 第5页共6页
第 5 页 共 6 页 五、解矩阵方程 AX=B 其中 − = − − = 1 0 1 1 1 1 2 1 1 , B 0 2 1 1 2 1 1 0 1 A 。(6’) 六、当 a 为何值时,线性方程组 − − + + = − + − − = + − + + = − + − − = 11 5 4 4 2 6 3 3 1 5 2 1 3 2 2 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x a x x x x x x x x 有解,并求出此时方程组的解。(8’) 得分 评卷人 得分 评卷人
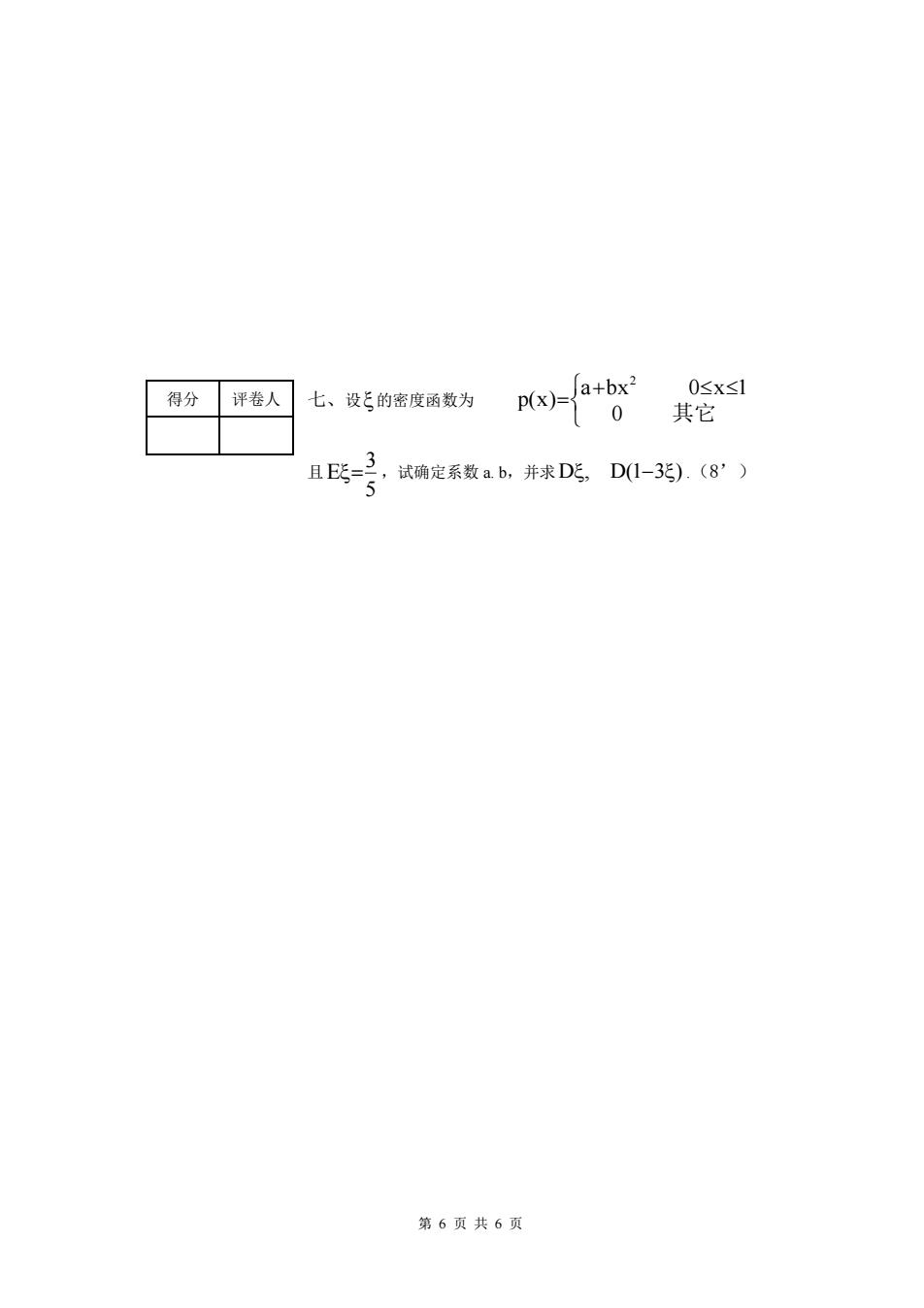
得分评卷人 七、设ξ的密度函数为 P) 0≤x≤1 且E氏=2,试确定系数ab,并求DE,D1-3).(8”) 5 第6页共6页
第 6 页 共 6 页 七、设 的密度函数为 + = 0 其它 a bx 0 x 1 p(x) 2 且 5 3 E= ,试确定系数 a. b,并求 D, D(1−3).(8’) 得分 评卷人