
呼和浩特职业学院 20082009学年第一学期高等数学试卷(A) 注意事项:1、本试卷共6页,满分100分,考试时间为120_分钟。 2、答题时请使用蓝、黑钢笔或圆珠笔。 3、考试形式:闭卷(开、闭) 项目 二 四五六 七总分 得分 得分评卷人 一、洗择颗:(20) 小设y=f国在区间0止有定义,则c+月+f-子的定义域是( A、0, c 2、函数=bg.k+F+可是( ) A、偶函数:B、奇函数: C、非奇非偶函数:D、既是奇又是偶函数 3、函数f(x)=0g:(-2x2+5x+3)的单调递减区间是() A(-0,)B[匠,+o)C(-支,) D[,3) 4、设某商品需求量对价格P的函数关系是Q=八p)=kd依,a为常数),则需求 量P对价格P的弹性是( A、pha B、na C、kaha D、kat 5、方程y-2m是( ) A、可分离变量的微分方程 B、齐次微分方程 C、一阶线性微分方程 D、以上三个都不对 6、下列广义积分收敛的是( ) 第1页共6页
第 1 页 共 6 页 呼和浩特职业学院 2008 ~2009 学年第一学期高等数学试卷(A) 注意事项:1、本试卷共 6 页,满分 100 分,考试时间为 120 分钟。 2、答题时请使用蓝、黑钢笔或圆珠笔。 3、考试形式: 闭 卷(开、闭) 项 目 一 二 三 四 五 六 七 总分 得 分 得分 评卷人 一、选择题:(20’) 1、设 y = f (x) 在区间[0,1]上有定义,则 ) 4 1 ) ( 4 1 f (x + + f x − 的定义域是( ) A、[0,1] B、 ] 4 5 , 4 1 [− C、 ] 4 1 , 4 1 [− D、 ] 4 3 , 4 1 [ 2、函数 log ( 1) 2 y = n x + x + 是( ) A、偶函数; B、奇函数; C、非奇非偶函数;D、既是奇又是偶函数 3、函数 ( ) log ( 2 5 3) 2 2 f x = 1 − x + x + 的单调递减区间是( ) A ( , ) 4 5 − B [ , ) 4 5 + C ( , ) 4 5 2 1 − D [ ,3) 4 5 4、设某商品需求量 Q 对价格 p 的函数关系是 Q = f ( p) = kap (k,a为常数) ,则需求 量 Q 对价格 p 的弹性是( ) A、 p ln a B、ln a C、 ka a p ln +1 D、 p+1 ka 5、方程 2 是 2 2 x y xy y − + = ( ) A、可分离变量的微分方程 B、齐次微分方程 C、一阶线性微分方程 D、以上三个都不对 6、下列广义积分收敛的是( ) .装.订.线. 班级 学号 姓名 密 封 线 内 不 要 答 题

3a14a1-a2-a1s 7、若D=aa=M,而D,=3a4a1-a2 ,则D=( aa an aa 3a14a31-a2-a3 A.3M B.-3M C.12M D.-12M 「2+122] 8、当=()时,111的秩为2。 112 A、0 B、1 C、2 D、3 9、设AB表示二事件,则下面结论中错误的是( A.A+B=AB+B B.AB=A+B C.若ACB,则A=AB D.若ACB,则AB 10、设随机变量5服从正态分布N(0,4),则P5<1}=() 人左 B∫6e e D点应杰 得分评卷人 二、填空题:(16) 1、设f八-》=2则+)- 2-9 =e,则c= 3、a=一,b=_时,函数y=a2+b在点x=1处有极大值1。 4设r0=1则0 5、心-妆= 第2页共6页
第 2 页 共 6 页 A、 + 1 1 dx x B、 + 0 + 2 1 dx x x C、 + 1 ln dx x x D、 + 1 3 1 dx x 7、若 M a a a a a a a a a D = = 31 32 33 21 22 23 11 12 13 ,而 3 1 3 1 3 2 3 3 2 1 2 1 2 2 2 3 1 1 1 1 1 2 1 3 1 3a 4a a a 3a 4a a a 3a 4a a a D − − − − − − = ,则 D1=( )。 A. 3M B. -3M C. 12M D. -12M 8、当 =( )时, + 1 1 2 1 1 1 1 2 2 的秩为 2。 A、0 B、1 C、2 D、3 9、设 A. B 表示二事件,则下面结论中错误的是( ) A. A+B=AB+B B. AB=A+B C. 若 AB ,则 A=AB D.若 AB ,则 AB 10、设随机变量 服从正态分布 N( 0 , 4 ) ,则 P{ 1} = ( ) A. dx x 1 − 0 8 2 2 2 1 e π B. dx x 1 − 0 4 4 1 e C. 2 1 2 1 − e π D. dx x − − 2 1 2 2 2 1 e π 得分 评卷人 二、填空题:(16’) 1、设 2 1 1) 1 ( − − = x x x f ,则 f (x +1) = _。 2、 1 2 lim 1 − → = − e x c x x ,则 c = 。 3、 a =_,b =_时,函数 2 4 y = ax + bx 在点 x =1 处有极大值 1。 4、设 (1) 1 ' f = ,则 = − − → 1 ( ) (1) lim 2 1 x f x f x _。 5、 − = xdx 2 0 1 _

6、若A是3阶方阵,且A=3,A”是A的伴随矩阵,则3A- 入、甲乙二人立地同时破译密码。甲破译的概率为,乙破译的概率为了,则该密码技破译 的概率为 得分评卷人 三、计算题:(34) [司 i 3设y-g管-0+m,求y04【emh 5、求由方程e-xy=0所确定的函数的微分。 第3页共6页
第 3 页 共 6 页 6、若 A 是 3 阶方阵,且 A =3, A * 是 A 的伴随矩阵,则 3A * = 。 7、甲乙二人独立地同时破译密码,甲破译的概率为 2 1 ,乙破译的概率为 3 1 ,则该密码被破译 的概率为_。 8、设离散型随机变量 X 的分布律为 ( = ) = , k = 1,2,3,4,5 a k P X k ,则 a = _。 得分 评卷人 三、计算题:(34’) 1、 − → x − x x x ln 1 1 lim 1 2、 x e e x x x 2 0 sin 2 lim + − − → 3、设 x x e x y x 3(1 ) arctan cos 2 = − + ,求 (0) ' y . 4、 + 4 0 2 1 e dx x 5、求由方程 e − xy = 0 y x 所确定的函数的微分

6、设xe为f(x)的一个原函数,求「xf(x)dk。 7、求微分方程y-ytanx=x的通解。 得分评卷人 四、某砖厂每月生产x(万块)砖的边际总成本C'(x)=4+】(千元万块), 边际总收入R(x)=8-x(千元/万块),试求:(1)月产量由1万块增加到5万块时月总成 本、总收入各增加多少?(2)月产量多少时月总利润最大?(6) 第4页共6页
第 4 页 共 6 页 6、设 x xe 为 f (x) 的一个原函数,求 xf (x)dx ' 。 7、求微分方程 y − y tan x = x ' 的通解。 四、某砖厂每月生产 x(万块)砖的边际总成本 4 ( ) 4 ' x C x = + (千元/万块), 边际总收入 R (x) = 8 − x ' (千元/万块),试求:(1)月产量由 1 万块增加到 5 万块时月总成 本、总收入各增加多少?(2)月产量多少时月总利润最大?(6’) 得分 评卷人
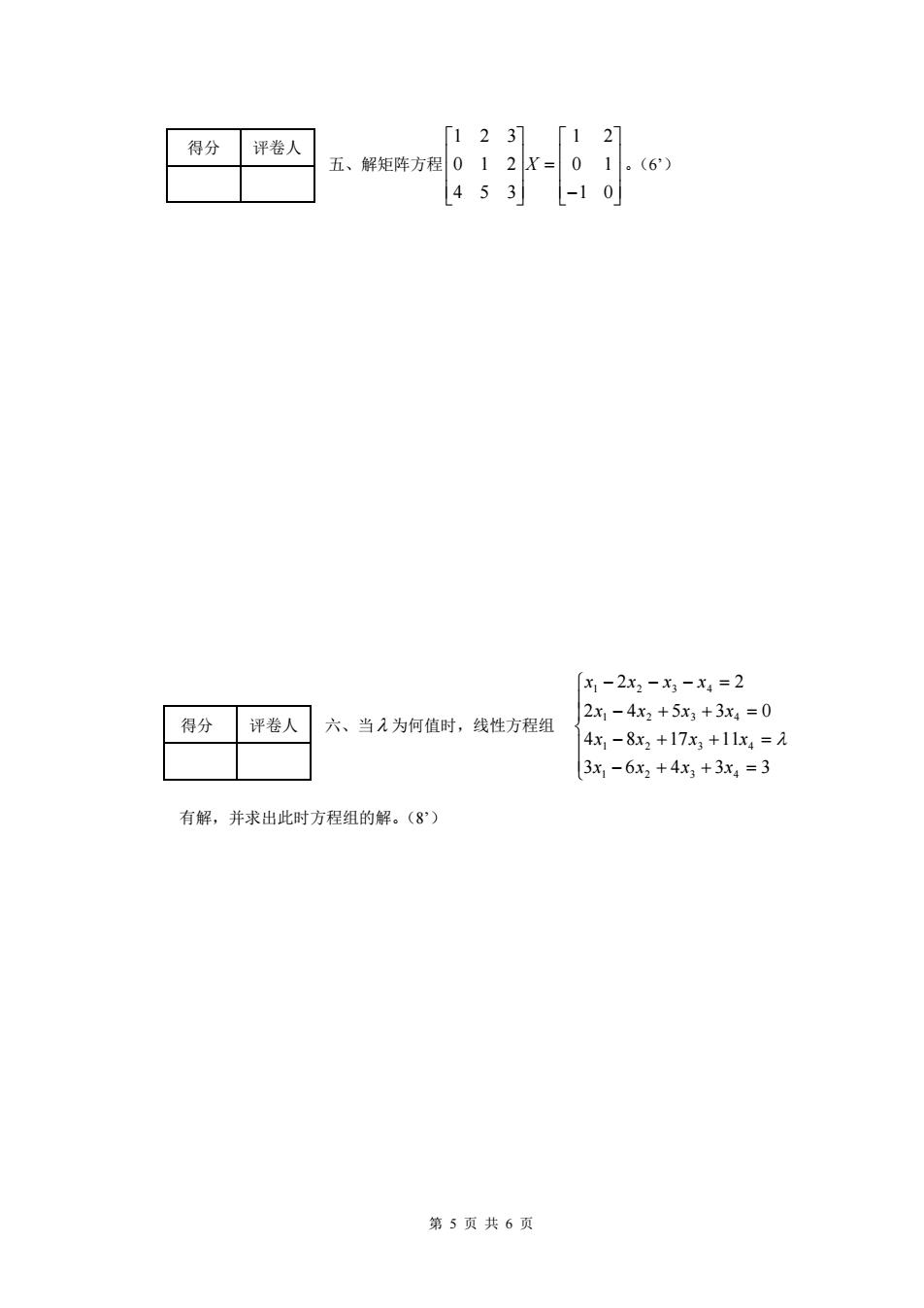
得分评卷人 「123]「12] 五、解矩阵方程012X=01(6 453-10 x-2x2-x3-x4=2 得分评卷人 六、当入为何值时,线性方程组 2x1-4x2+5x3+3x4=0 4-8x2+17x+1x4=2 3x,-6x2+4x1+3x4=3 有解,并求出此时方程组的解。(8) 第5页共6页
第 5 页 共 6 页 五、解矩阵方程 − = 1 0 0 1 1 2 4 5 3 0 1 2 1 2 3 X 。(6’) 六、当 为何值时,线性方程组 − + + = − + + = − + + = − − − = 3 6 4 3 3 4 8 17 11 2 4 5 3 0 2 2 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x x x x x 有解,并求出此时方程组的解。(8’) 得分 评卷人 得分 评卷人
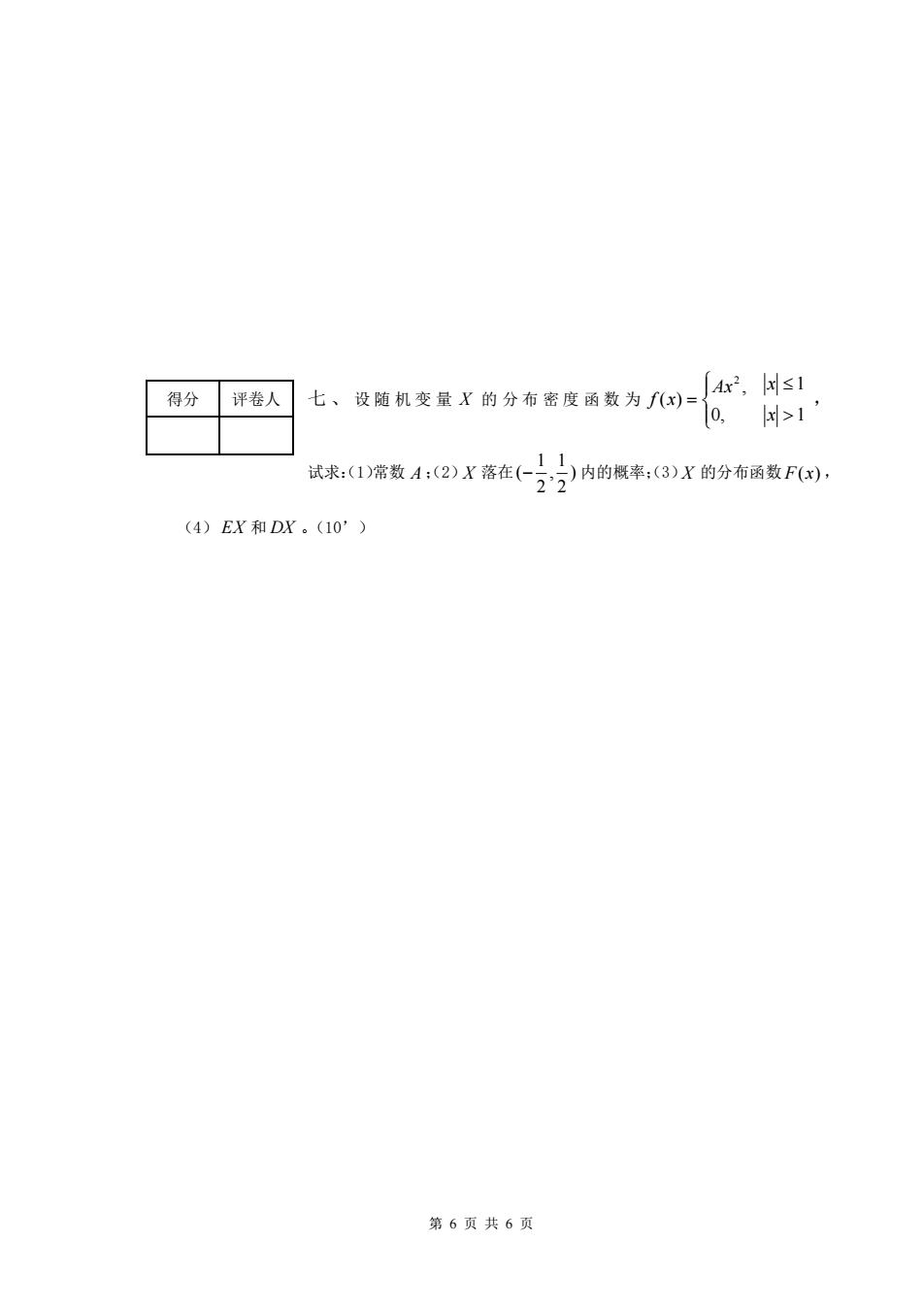
得分评卷人 七、设随机变量X的分布密度函数为(x)= Ax,s1 0,d>11 (4)EX和DX。(10') 第6页共6页
第 6 页 共 6 页 七 、 设 随 机 变 量 X 的 分 布 密 度 函 数 为 = 1 1 0, , ( ) 2 x Ax x f x , 试求:(1)常数 A ;(2) X 落在 1 1 ( , ) 2 2 − 内的概率;(3) X 的分布函数 F(x) , (4) EX 和 DX 。(10’) 得分 评卷人