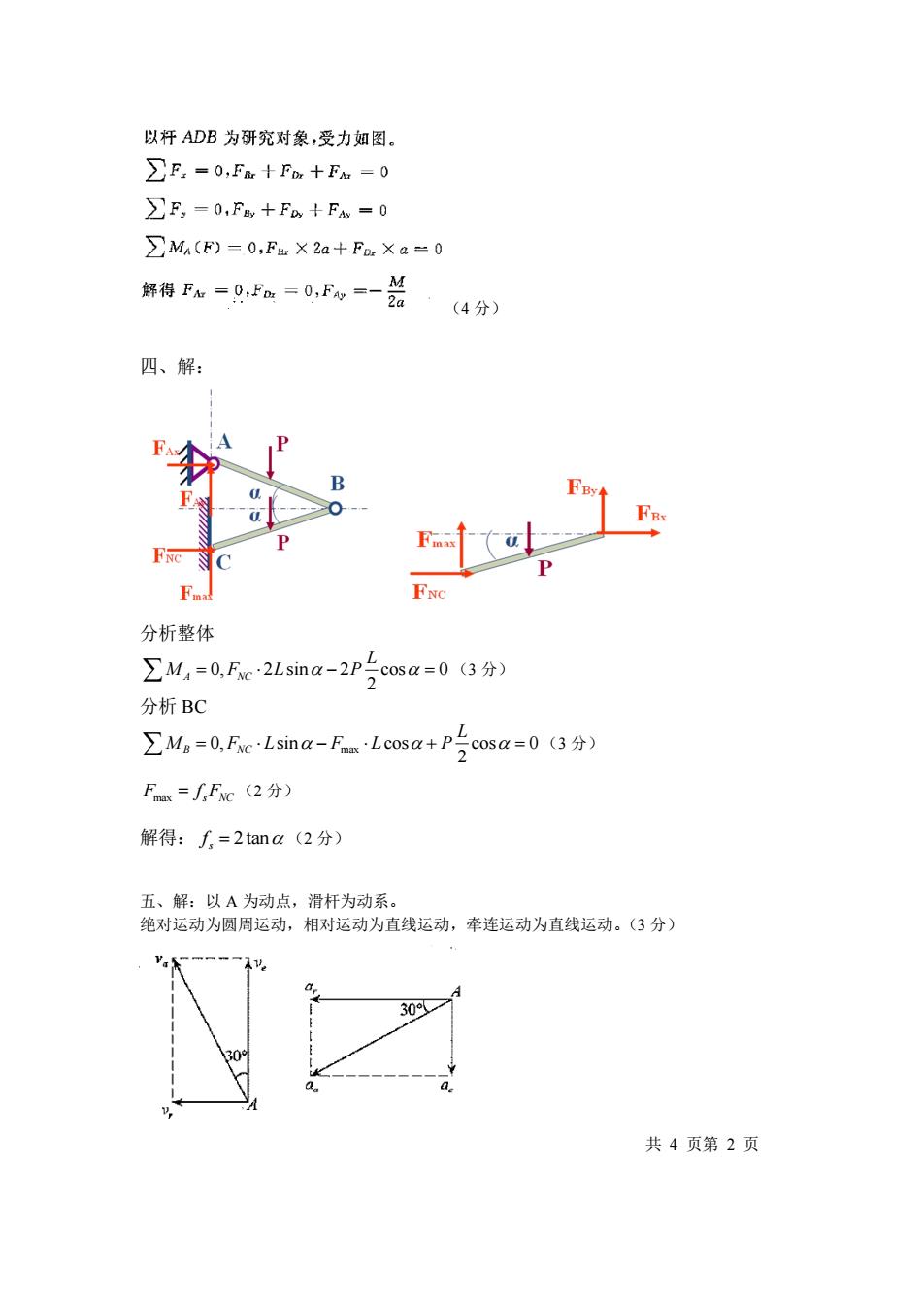
以杆ADB为研究对象，受力如图。 ∑P,=0,Fm十F,十Fa=0 ∑F,=0,PF+F+FA-0 >MA(F)=0,Fu X 2a+For Xa-0 邻得Pa=0Fa=0,Fw=一兰 ·(4分) 四、解： B FBs FNc 分析整体 ∑M4=0,Fc·2 Lsina-2p5。 cosa=0(3分) 分析BC ∑Ma=0,FcLsina-FLcosa+posa=0(3分) ) F=fFc(2分) 解得：f,=2tana(2分) 五、解：以A为动点，滑杆为动系。 绝对运动为圆周运动，相对运动为直线运动，牵连运动为直线运动。(3分) 30 30 共4页第2页（4 分） 四、解： 分析整体 0, 2 sin 2 cos 0 2 A NC L  M F L P =  − =   （3 分） 分析 BC max 0, sin cos cos 0 2 B NC L  M F L F L P =  −  + =    （3 分） F f F max = s NC （2 分） 解得： 2 tan s f =  （2 分） 五、解：以 A 为动点，滑杆为动系。 绝对运动为圆周运动，相对运动为直线运动，牵连运动为直线运动。（3 分） 共 4 页第 2 页