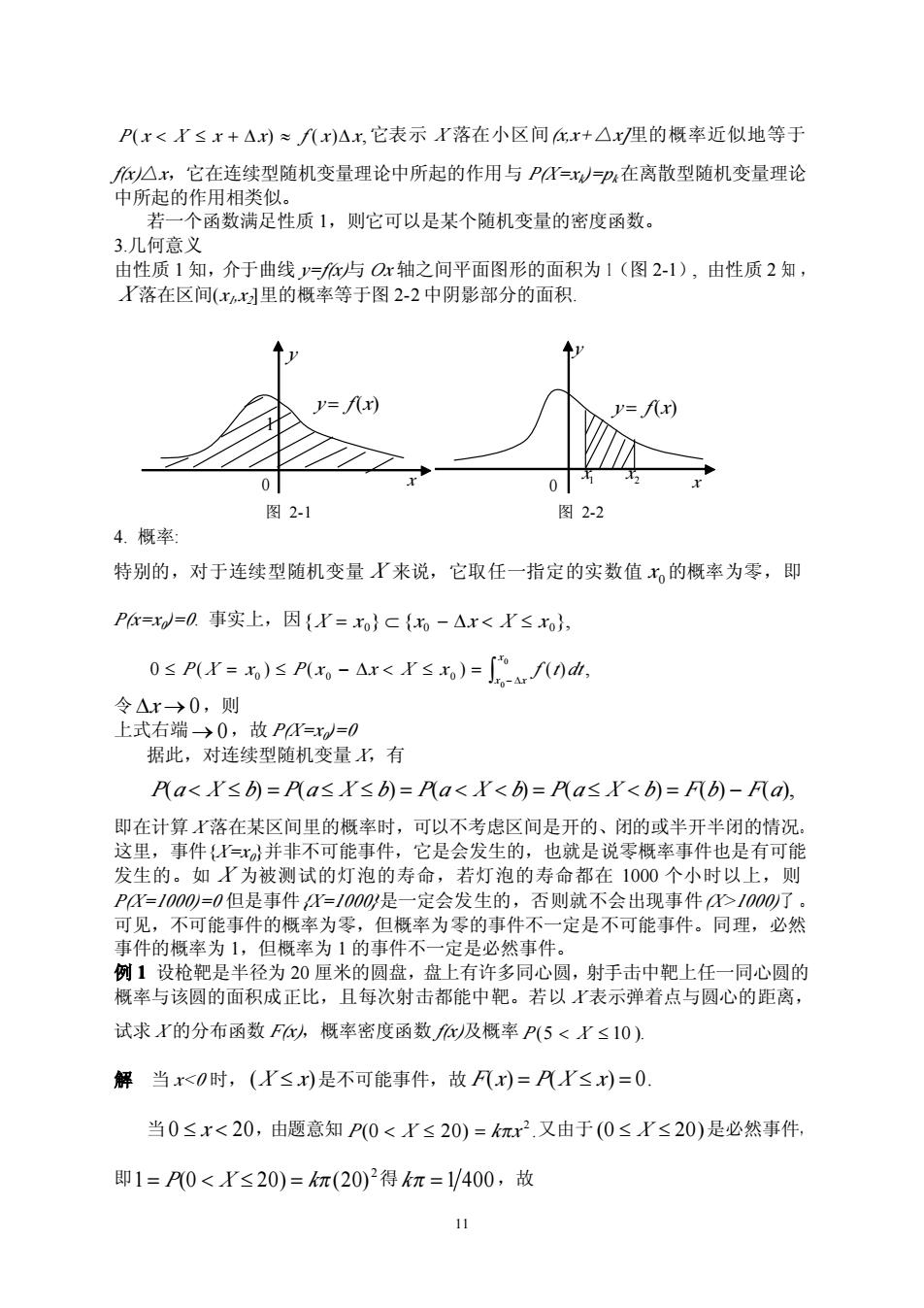
P(x<X≤x+△x)≈f八x)△x,它表示X落在小区间r+△x里的概率近似地等于 你)△x,它在连续型随机变量理论中所起的作用与P=x=p在离散型随机变量理论 中所起的作用相类似。 若一个函数满足性质1，则它可以是某个随机变量的密度函数。 3.几何意义 由性质1知，介于曲线y=f与Ox轴之间平面图形的面积为1（图2-1），由性质2知， X落在区间(x,x里的概率等于图2-2中阴影部分的面积 y=f八x) =fx) 0 0 图2-1 图2-2 4.概率： 特别的，对于连续型随机变量厂来说，它取任一指定的实数值x的概率为零，即 Pr=x=O.事实上，因{r=xo}C{-△x<≤xo}, 0≤P(X=)≤Px-Ar<X≤x)=Af0山， 令△x→0，则 上式右端→0，故P=x=0 据此，对连续型随机变量K,有 P\a<X≤=Pa≤X≤b=Pa<X<)=Pa≤r<)=Fb)-Fa, 即在计算X落在某区间里的概率时，可以不考虑区间是开的、闭的或半开半闭的情况。 这里，事件{=x}并非不可能事件，它是会发生的，也就是说零概率事件也是有可能 发生的。如'为被测试的灯泡的寿命，若灯泡的寿命都在1000个小时以上，则 PX=1000)=0但是事件X=1000是一定会发生的，否则就不会出现事件>1000了。 可见，不可能事件的概率为零，但概率为零的事件不一定是不可能事件。同理，必然 事件的概率为1，但概率为1的事件不一定是必然事件。 例1设枪靶是半径为20厘米的圆盘，盘上有许多同心圆，射手击中靶上任一同心圆的 概率与该圆的面积成正比，且每次射击都能中靶。若以X表示弹着点与圆心的距离， 试求r的分布函数F,概率密度函数)及概率P(5<X≤10) 解当x<O时，（≤x)是不可能事件，故Fx)=P八≤x)=0 当0≤x<20,由题意知P(0<X≤20)=kπx2.又由于(0≤X≤20)是必然事件， 即1=P0<r≤20)=π(20)2得kπ=1/400，故 1111 P( x  X  x  x)  f ( x )x, 它表示 X 落在小区间(x,x+△x]里的概率近似地等于 f(x)△x，它在连续型随机变量理论中所起的作用与 P(X=xk)=pk在离散型随机变量理论 中所起的作用相类似。 若一个函数满足性质 1，则它可以是某个随机变量的密度函数。 3.几何意义 由性质 1 知，介于曲线 y=f(x)与 Ox 轴之间平面图形的面积为 1（图 2-1）, 由性质 2 知 ， 落在区间(x1,x2 X ]里的概率等于图 2-2 中阴影部分的面积. 4. 概率: 特别的，对于连续型随机变量 X 来说，它取任一指定的实数值 x 0的概率为零，即 P(x=x0)=0. 事实上，因{ } { }, 0 0 0 X  x  x  x  X  x 0 ( ) ( ) ( ) , 0 0 0 0 0            x x x P X x P x x X x f t dt 令 x  0，则 上式右端 ，故 P(X=x0  0 )=0 据此，对连续型随机变量 X，有 P(a  X  b)  P(a  X  b)  P(a  X  b)  P(a  X  b)  F(b)  F(a), 即在计算 X 落在某区间里的概率时，可以不考虑区间是开的、闭的或半开半闭的情况。 这里，事件{X=x0}并非不可能事件，它是会发生的，也就是说零概率事件也是有可能 发生的。如 X 为被测试的灯泡的寿命，若灯泡的寿命都在 1000 个小时以上，则 P(X=1000)=0 但是事件{X=1000}是一定会发生的，否则就不会出现事件(X>1000)了 。 可见，不可能事件的概率为零，但概率为零的事件不一定是不可能事件。同理，必然 事件的概率为 1，但概率为 1 的事件不一定是必然事件。 例 1 1 设枪靶是半径为 20 厘米的圆盘，盘上有许多同心圆，射手击中靶上任一同心圆的 概率与该圆的面积成正比，且每次射击都能中靶。若以 X 表示弹着点与圆心的距离， 试求 X 的分布函数 F(x)，概率密度函数 f(x)及概率 P(5  X  10 ). 解 当 x<0 时， (X  x)是不可能事件，故 F( x)  P(X  x)  0. 当 0  x  20，由题意知 P(0  X  20)  kx 2 .又由于 (0  X  20)是必然事件， 即1  P(0  X  20)  k(20) 2得 k 1 400，故 y x 0 1 y  f (x) 图 2-1 y x 0 1 x 2 x y  f (x) 图 2-2