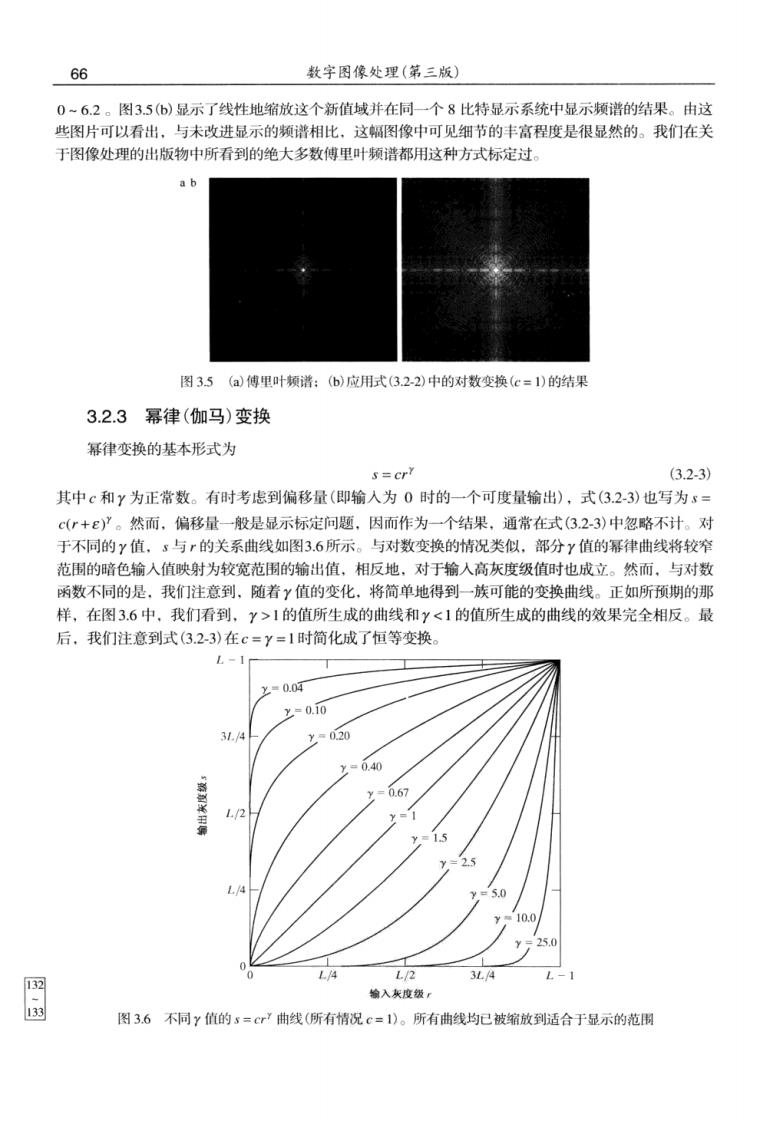
66 数字图像处理（第三版） 0一6.2。图35(6)显示了线性地缩放这个新值域并在同一个8比特显示系统中显示频谱的结果。由这 些图片可以看出，与未改进显示的频谱相比.这幅图像中可见细节的丰富程度是很显然的。我们在关 于图像处理的出版物中所看到的绝大多数傅里叶颜谱都用这种方式标定过。 ab 图35(a)傅里叶频谱：(b)应用式(3.2-2)中的对数变换(c=1)的结果 3.2.3幂律（加马）变换 幂律变换的基本形式为 s=cr (323) 其中c和y为正常数。有时考虑到偏移量（即输入为0时的一个可度量输出），式(3.23)也写为s c(r+ε了。然而，偏移量一般是显示标定问题，因而作为一个结果.通常在式3.2-3)中忽略不计。对 于不同的y值，s与r的关系曲线如图3.6所示 与对数变换的情祝类似，部分Y值的幂律曲线将较 范围的暗色输入值映射为较宽范围的输出值，相反地，对于输人高灰度级值时也成立。然而，与对数 函数不同的是，我们注意到.随着Y值的变化，将简单地得到一族可能的变换曲线。正如所预期的那 样，在图3.6中，我们看到，Y>1的值所生成的曲线和y<1的值所生成的曲线的效果完全相反。最 后，我们注意到式(3.23)在c=Y=1时简化成了恒等变换。 L-1 y=0.10 31. 040 667 15 2 入灰度级 图36不同y值的s='曲线（所有情况c=)。所有曲线均已被缩放到适合于显示的范围