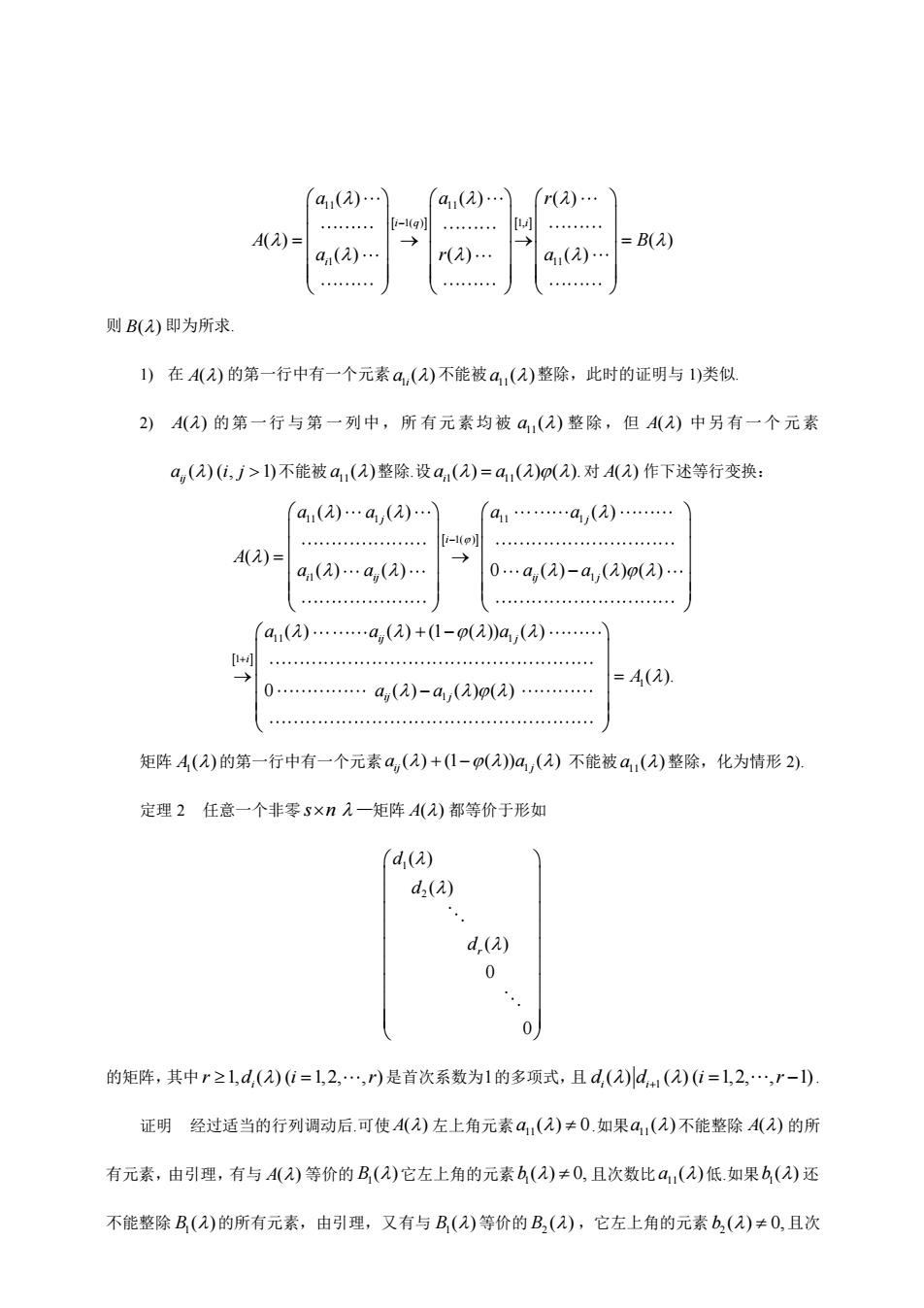
a(). a().）r().） 4A)= =B(2) a(2). r(2). a(2). 则B()即为所求 1)在A()的第一行中有一个元素a,()不能被a,(2)整除，此时的证明与1)类似 2)A()的第一行与第一列中，所有元素均被4，()整除，但A)中另有一个元素 a,(2)(，j广>)不能被a,(a)整除设a(2)=a,()(2).对A(2)作下述等行变换 a(2).a(a).） a.a,(2). 4A(2)= a().a,(2) 0.a,()-a,((2) a(2).a(2)+(1-p()a(2).】 =A(a). 0.a,(2)-a(a0p(2). 矩阵A()的第一行中有一个元素a,(a)+(1-p)a,()不能被a,(2)整除，化为情形2) 定理2任意一个非零s×n入一矩阵A()都等价于形如 d,(a) d2(2) d.(a) 0 0 的矩阵，其中r21,d,(2)0=1,2,.,r)是首次系数为1的多项式，且d()d(2)(i=1,2,.,r-1) 证明经过适当的行列调动后.可使A()左上角元素a,(2)≠0.如果a,(2)不能整除A()的所 有元素，由引理，有与A2)等价的B()它左上角的元素b(a)≠0，且次数比a,()低如果6()还 不能整除B(2)的所有元素，由引理，又有与B,()等价的B,(),它左上角的元素b,()≠0，且次    11 11 1( ) 1, 1 11 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) i q i i a a r A B a r a         −                   = → → =                     则 B( )  即为所求. 1) 在 A( )  的第一行中有一个元素 1 ( ) i a  不能被 11 a ( )  整除，此时的证明与 1)类似. 2) A( )  的第一行与第 一列中，所 有元素均被 11 a ( )  整除，但 A( )  中另有一个 元素 ( ) ( , 1) ij a i j   不能被 11 a ( )  整除.设 1 11 ( ) ( ) ( ). i a a     = 对 A( )  作下述等行变换：     11 1 11 1 1( ) 1 1 11 1 1 ( ) ( ) ( ) ( ) ( ) ( ) 0 ( ) ( ) ( ) ( ) ( ) (1 ( )) ( ) 0 j j i i ij ij j ij j i i a a a a A a a a a a a a a                 − +         = → −     + − → 1 1 ( ). ( ) ( ) ( ) j j A a          = −   矩阵 1 A ( )  的第一行中有一个元素 1 ( ) (1 ( )) ( ) ij j a a     + − 不能被 11 a ( )  整除，化为情形 2). 定理 2 任意一个非零 s n  —矩阵 A( )  都等价于形如 1 2 ( ) ( ) ( ) 0 0 r d d d          的矩阵，其中 1, ( ) ( 1,2, , ) i r d i r  =  是首次系数为 1 的多项式，且 1 ( ) ( ) ( 1,2, , 1) i i d d i r   + = − . 证明 经过适当的行列调动后.可使 A( )  左上角元素 11 a ( ) 0   .如果 11 a ( )  不能整除 A( )  的所 有元素，由引理，有与 A( )  等价的 1 B ( )  它左上角的元素 1 b ( ) 0,   且次数比 11 a ( )  低.如果 1 b ( )  还 不能整除 1 B ( )  的所有元素，由引理，又有与 1 B ( )  等价的 2 B ( )  ，它左上角的元素 2 b ( ) 0,   且次