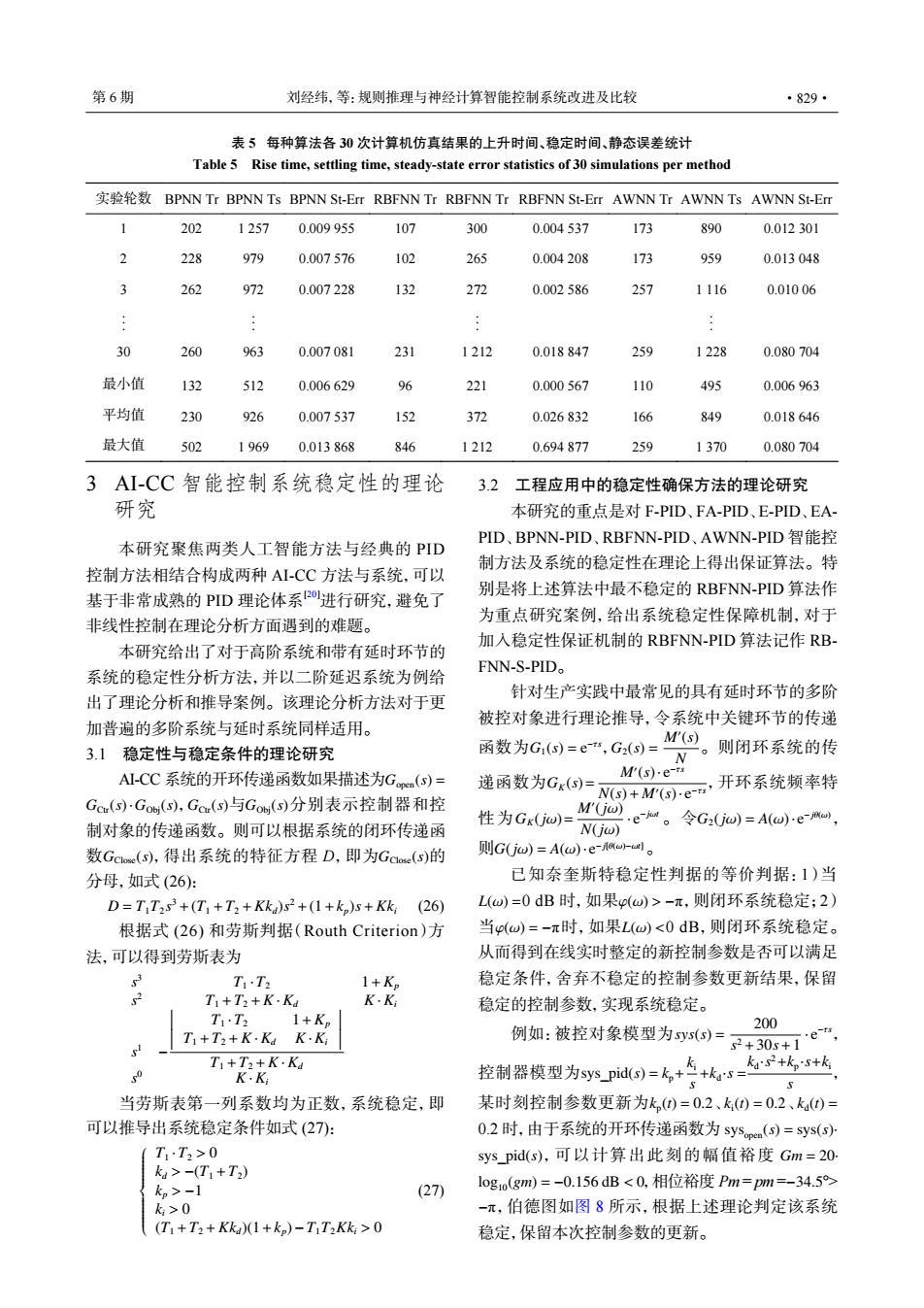
第6期 刘经纬，等：规则推理与神经计算智能控制系统改进及比较 ·829· 表5每种算法各30次计算机仿真结果的上升时间、稳定时间、静态误差统计 Table 5 Rise time,settling time,steady-state error statistics of 30 simulations per method 实验轮数BPNN Tr BPNN Ts BPNN St-Err RBFNN Tr RBFNN Tr RBFNN St-.Err AWNN Tr AWNN Ts AWNN St-ET 1 202 1257 0.009955 107 300 0.004537 173 890 0.012301 2 228 979 0.007576 102 265 0.004208 173 959 0.013048 3 262 972 0.007228 132 272 0.002586 257 1116 0.01006 30 260 963 0.007081 231 1212 0.018847 259 1228 0.080704 最小值 132 512 0.006629 96 221 0.000567 110 495 0.006963 平均值 230 926 0.007537 152 372 0.026832 166 849 0.018646 最大值 502 1969 0.013868 846 1212 0.694877 259 1370 0.080704 3AI-CC智能控制系统稳定性的理论 3.2 工程应用中的稳定性确保方法的理论研究 研究 本研究的重点是对F-PID、FA-PID、E-PID、EA PID、BPNN-PID、RBFNN-PID、AWNN-PID智能控 本研究聚焦两类人工智能方法与经典的PID 制方法及系统的稳定性在理论上得出保证算法。特 控制方法相结合构成两种AI-CC方法与系统，可以 基于非常成熟的PID理论体系2进行研究，避免了 别是将上述算法中最不稳定的RBFNN-PID算法作 非线性控制在理论分析方面遇到的难题。 为重点研究案例，给出系统稳定性保障机制，对于 本研究给出了对于高阶系统和带有延时环节的 加入稳定性保证机制的RBFNN-PID算法记作RB, 系统的稳定性分析方法，并以二阶延迟系统为例给 FNN-S-PIDo 出了理论分析和推导案例。该理论分析方法对于更 针对生产实践中最常见的具有延时环节的多阶 加普遍的多阶系统与延时系统同样适用。 被控对象进行理论推导，令系统中关键环节的传递 3.1稳定性与稳定条件的理论研究 函数为G)=e”,G)=MW0。则闭环系统的传 A.CC系统的开环传递函数如果描述为Gpm(s)= M'(s).e-rs Gc(S)·Go(s),Gc(s)与Go(s)分别表示控制器和控 递函数为Cr⊙)四+MS-c,开环系统频率特 制对象的传递函数。则可以根据系统的闭环传递函 性为Gx(jd)= M'(jo) em。令G2(jd)=A(）eu, N(iw) 数Gce(,得出系统的特征方程D,即为Gaoe(s)的 则G(j）)=A(w）e-aa-u。 分母，如式(26)： 已知奈奎斯特稳定性判据的等价判据：1)当 D=TT2s3+(T1+T2+Kk)s2+(1+k)s+Kk(26) L(w)=0dB时，如果p()>-π，则闭环系统稳定；2) 根据式(26)和劳斯判据(Routh Criterion)方 当p(w)=-π时，如果L(ω)<0dB,则闭环系统稳定。 法，可以得到劳斯表为 从而得到在线实时整定的新控制参数是否可以满足 T1·T2 1+Kp 稳定条件，舍弃不稳定的控制参数更新结果，保留 T1+T2+K·Ka K·K 稳定的控制参数，实现系统稳定。 T1·T3 1+Kp 200 T1+T2+K.Ka K.K; 例如：被控对象模型为sys(s)= s 2+30s+e”, T1+T2+K·K 控制器模型为kys_pid(s)=+冬s--+s+长 k so K·K: 当劳斯表第一列系数均为正数，系统稳定，即 某时刻控制参数更新为k,(0=0.2、k()=02、k()= 可以推导出系统稳定条件如式(27)： 0.2时，由于系统的开环传递函数为SYSope(s)=sys(s) T1T2>0 sys_pid(s),可以计算出此刻的幅值裕度Gm=20 k>-(T1+T) k2>-1 (27) 1og1o(gm）=-0.156dB<0,相位裕度Pm=pm=-34.5 k>0 -π，伯德图如图8所示，根据上述理论判定该系统 (T1+T2+Kk)(1+ke)-T1T2Kk>0 稳定，保留本次控制参数的更新。3 AI-CC 智能控制系统稳定性的理论 研究 本研究聚焦两类人工智能方法与经典的 PID 控制方法相结合构成两种 AI-CC 方法与系统，可以 基于非常成熟的 PID 理论体系[20]进行研究，避免了 非线性控制在理论分析方面遇到的难题。 本研究给出了对于高阶系统和带有延时环节的 系统的稳定性分析方法，并以二阶延迟系统为例给 出了理论分析和推导案例。该理论分析方法对于更 加普遍的多阶系统与延时系统同样适用。 3.1 稳定性与稳定条件的理论研究 Gopen(s) = GCtr(s)·GObj(s) GCtr(s) GObj(s) GClose(s) GClose(s) AI-CC 系统的开环传递函数如果描述为 ， 与 分别表示控制器和控 制对象的传递函数。则可以根据系统的闭环传递函 数 ，得出系统的特征方程 D，即为 的 分母，如式 (26)： D = T1T2 s 3 +(T1 +T2 +Kkd)s 2 +(1+kp)s+Kki (26) 根据式 (26) 和劳斯判据（Routh Criterion）方 法，可以得到劳斯表为 s 3 T1 ·T2 1+Kp s 2 T1 +T2 +K ·Kd K ·Ki s 1 −       T1 ·T2 1+Kp T1 +T2 +K ·Kd K ·Ki       T1 +T2 +K ·Kd s 0 K ·Ki 当劳斯表第一列系数均为正数，系统稳定，即 可以推导出系统稳定条件如式 (27)：    T1 ·T2 > 0 kd > −(T1 +T2) kp > −1 ki > 0 (T1 +T2 +Kkd)(1+kp)−T1T2Kki > 0 (27) 3.2 工程应用中的稳定性确保方法的理论研究 本研究的重点是对 F-PID、FA-PID、E-PID、EA￾PID、BPNN-PID、RBFNN-PID、AWNN-PID 智能控 制方法及系统的稳定性在理论上得出保证算法。特 别是将上述算法中最不稳定的 RBFNN-PID 算法作 为重点研究案例，给出系统稳定性保障机制，对于 加入稳定性保证机制的 RBFNN-PID 算法记作 RB￾FNN-S-PID。 G1(s) = e −τs G2(s) = M′ (s) N GK(s)= M′ (s)· e −τs N(s)+ M′ (s)· e −τs GK(jω)= M′ (jω) N(jω) · e −jωt G2(jω) = A(ω)· e −jθ(ω) G(jω) = A(ω)· e −j[θ(ω)−ωt] 针对生产实践中最常见的具有延时环节的多阶 被控对象进行理论推导，令系统中关键环节的传递 函数为 ， 。则闭环系统的传 递函数为 ，开环系统频率特 性为 。令 ， 则 。 L(ω) = φ(ω) > −π φ(ω) = −π L(ω) < 已知奈奎斯特稳定性判据的等价判据：1）当 0 dB 时，如果 ，则闭环系统稳定；2） 当 时，如果 0 dB，则闭环系统稳定。 从而得到在线实时整定的新控制参数是否可以满足 稳定条件，舍弃不稳定的控制参数更新结果，保留 稳定的控制参数，实现系统稳定。 sys(s) = 200 s 2 +30s+1 · e −τs sys_pid(s) = kp+ ki s +kd ·s = kd ·s 2+kp ·s+ki s kp(t) = 0.2 ki(t) = 0.2 kd(t) = sysopen(s) = sys(s)· sys_pid(s) Gm = 20· log10(gm) = −0.156 dB < 0 −34.5 −π 例如：被控对象模型为 ， 控制器模型为 ， 某时刻控制参数更新为 、 、 0.2 时，由于系统的开环传递函数为 ，可以计算出此刻的幅值裕度 ，相位裕度 Pm = pm = °> ，伯德图如图 8 所示，根据上述理论判定该系统 稳定，保留本次控制参数的更新。 表 5 每种算法各 30 次计算机仿真结果的上升时间、稳定时间、静态误差统计 Table 5 Rise time, settling time, steady-state error statistics of 30 simulations per method 实验轮数 BPNN Tr BPNN Ts BPNN St-Err RBFNN Tr RBFNN Tr RBFNN St-Err AWNN Tr AWNN Ts AWNN St-Err 1 202 1 257 0.009 955 107 300 0.004 537 173 890 0.012 301 2 228 979 0.007 576 102 265 0.004 208 173 959 0.013 048 3 262 972 0.007 228 132 272 0.002 586 257 1 116 0.010 06 . . . . . . . . . . . . 30 260 963 0.007 081 231 1 212 0.018 847 259 1 228 0.080 704 最小值 132 512 0.006 629 96 221 0.000 567 110 495 0.006 963 平均值 230 926 0.007 537 152 372 0.026 832 166 849 0.018 646 最大值 502 1 969 0.013 868 846 1 212 0.694 877 259 1 370 0.080 704 第 6 期 刘经纬，等：规则推理与神经计算智能控制系统改进及比较 ·829·