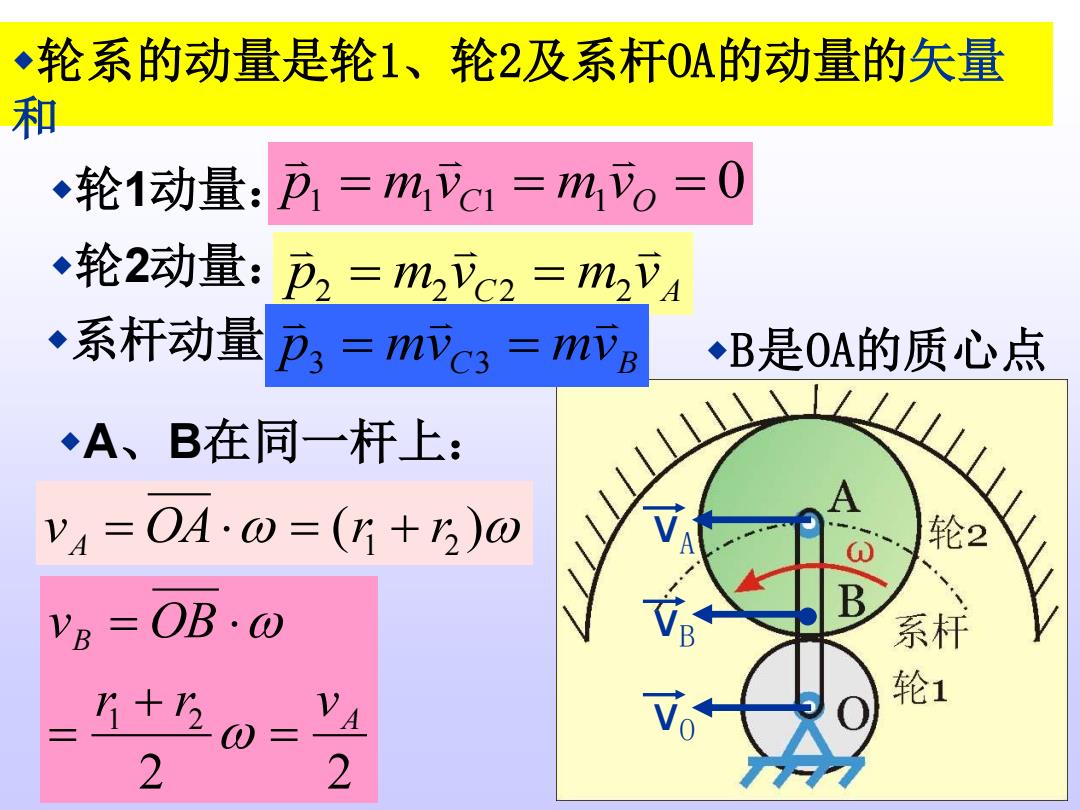
◆轮系的动量是轮1、轮2及系杆0A的动量的矢量 和 ◆轮1动量p1=mc1=mo=0 ◆轮2动量：D2=1m2c2三m24 ◆系杆动量D3=mc3=B ◆B是OA的质心点 ◆A、B在同一杆上： vA=OA·0=(行+3)ω 轮2 VB=OB· +2 VA 2 2轮系的动量是轮1、轮2及系杆OA的动量的矢量 和 p p1 p2 p3     轮1动量： = + + 系杆动量： p1 = m1 vC1 = m1 vO = 0    轮2动量： C A p m v m v    2 = 2 2 = 2 C B p mv mv    3 = 3 = A、B在同一杆上： vA = OA = (r1 + r2 ) 2 2 1 2 A B r r v v OB = + = =    vB vO vA B是OA的质心点