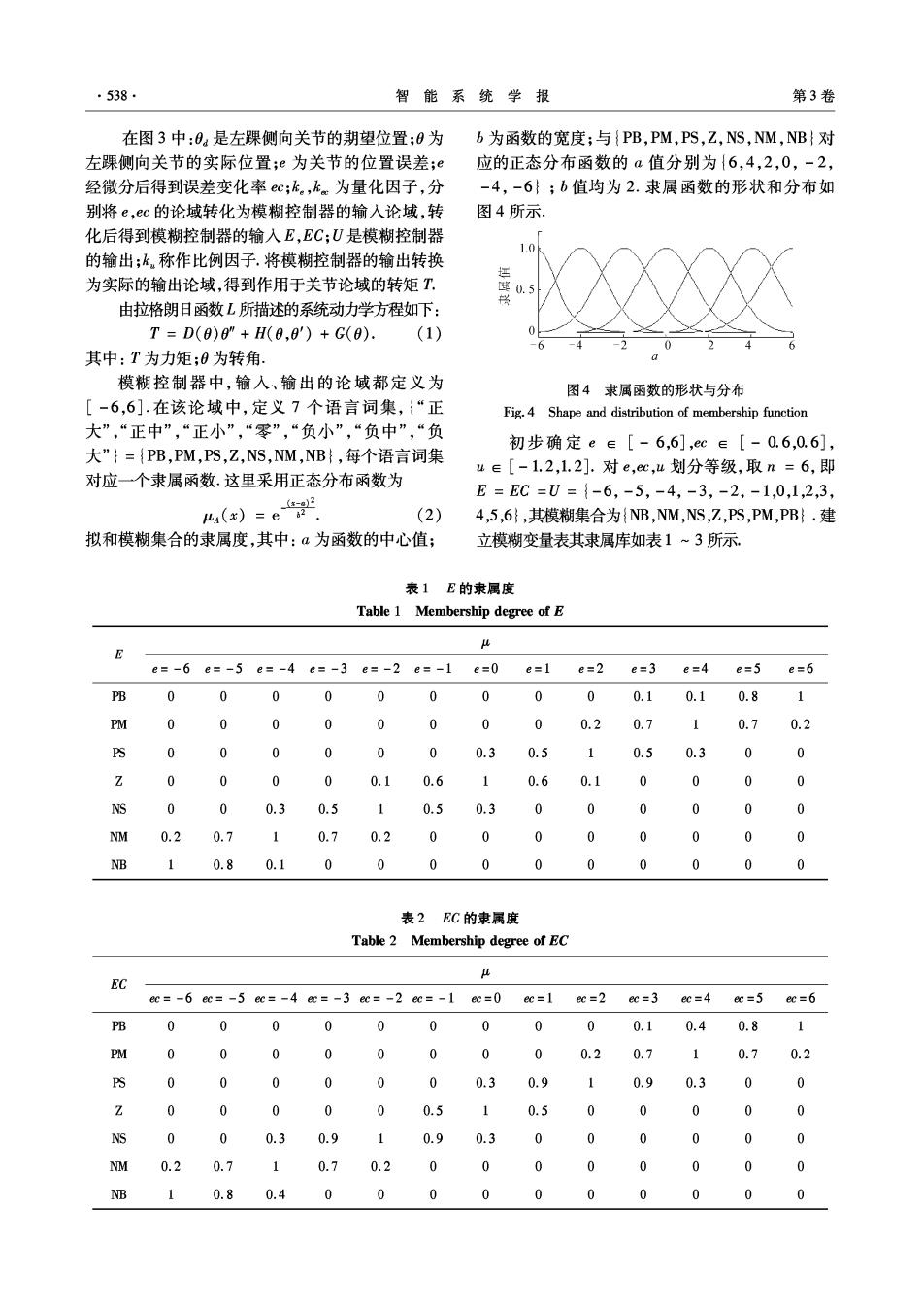
·538. 智能系统学报 第3卷 在图3中：0.是左踝侧向关节的期望位置；0为 b为函数的宽度；与{PB,PM,PS,Z,NS,NM,NB}对 左踝侧向关节的实际位置；e为关节的位置误差；e 应的正态分布函数的a值分别为{6,4,2,0，-2， 经微分后得到误差变化率ec;k。,k为量化因子，分 -4,-6};b值均为2.隶属函数的形状和分布如 别将e,ec的论域转化为模糊控制器的输入论域，转 图4所示. 化后得到模糊控制器的输入E,EC;U是模糊控制器 的输出；k,称作比例因子.将模糊控制器的输出转换 为实际的输出论域，得到作用于关节论域的转矩T, 0.9 由拉格朗日函数L所描述的系统动力学方程如下： T=D(0)8"+H(0,0)+G(0). (1) 其中：T为力矩；0为转角. 模糊控制器中，输入、输出的论域都定义为 图4隶属函数的形状与分布 [-6,6].在该论域中，定义7个语言词集，{“正 Fig.4 Shape and distribution of membership function 大”，“正中”，“正小”，“零”，“负小”，“负中”，“负 初步确定e∈[-6,6]，ec∈[-0.6,0.6]， 大”}={PB,PM,PS,Z,NS,NM,NB},每个语言词集 u∈[-1.2，l.2].对e,ec,4划分等级，取n=6,即 对应一个隶属函数.这里采用正态分布函数为 E=EC=U={-6,-5,-4,-3,-2,-1,0,1,2,3, _(x-a)2 ua(x)=e (2) 4,5,6},其模糊集合为{NB,NM,NS,Z,PS,PM,PB}.建 拟和模糊集合的隶属度，其中：a为函数的中心值； 立模糊变量表其隶属库如表1~3所示， 表1E的隶属度 Table 1 Membership degree of E e=-6e=-5e=-4e=-3 e=-2e=-1 e=0 e=1 e=2 e=3 e=4 e=5 e=6 PB 0 0 0 0 0 0 0 0 0 0.1 0.1 0.8 1 PM 0 0 0 0 0 0 0 0 0.2 0.7 0.7 0.2 PS 0 0 0 0 0.3 0.5 0.5 0.3 0 0 0 0.1 0.6 0.6 0.1 0 0 NS 0 0.3 0.5 0.5 0.3 0 0 0 NM 0.2 0.7 0.7 0.2 0 0 0 0 0 NB 1 0.8 0.1 0 0 0 0 0 0 0 0 表2EC的隶属度 Table 2 Membership degree of EC EC ee=-6ec=-5ec=-4=-3ee=-2ec=-1ec=0ec=1ee=2 ec=3 ec=4 ec=5 ec=6 PB 0 0 0 0 0 0 0 0 0.1 0.4 0.8 PM 0 0 0 0 0 0 0 0 0.2 0.7 0.7 0.2 S 0 0 0 0 0 0 0.3 0.9 0.9 0.3 0 0 Z 0 0 0 0 0 0.5 0.5 0 0 0 0 NS 0 0 0.3 0.9 0.9 0.3 0 0 0 0 0 NM 0.2 0.7 1 0.7 0.2 0 0 0 B 1 0.8 0.4 0 0 0 0 0 0 0 0 0