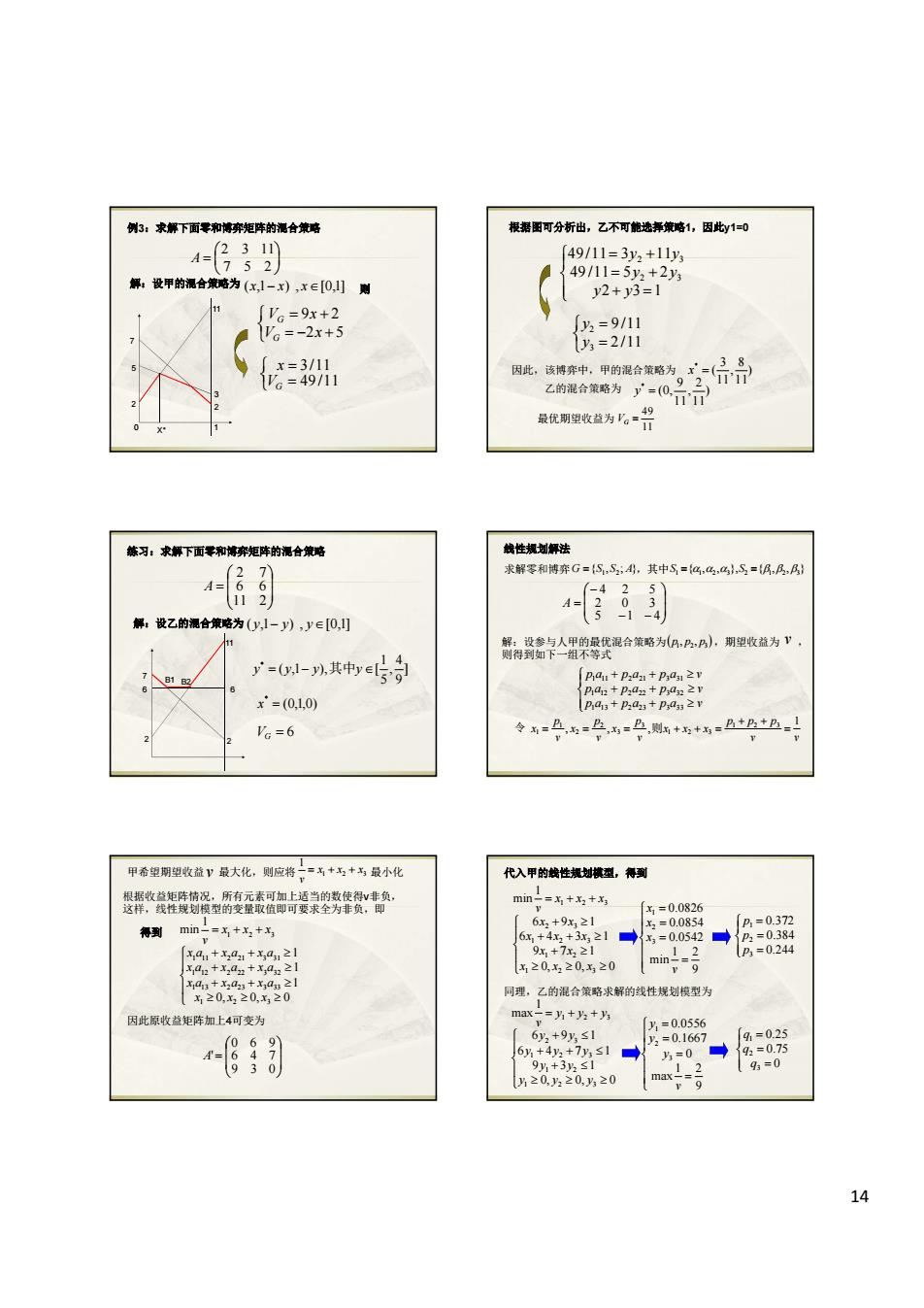
3：求解下面零和奔矩车的酒合 根据国可分析出，乙不可进舞略1，因y10 解设甲的合为 /11 3y:+ x,l-x),x∈0，J则 2+3=1 「V:=9x+2 AWVa=-2x+5 =9/11 =2/11 因此，该神弃中，甲的混合策略为 最优開望收益为 求解零和将奔G=5,5:,其中5=4，色，a5=民，风，风 解，设乙的覆合策略为(y,1-),y∈0，] 卓人用的温合策略为A,A。期塑收雅为Y 广-0-%其e x=(01,0 VG=6 ==与=则++=B卫=日 甲希细期塑收益最大化。则应将+名+最小化 代入甲的性提城，到 楼竹技克资定两变酸即装荣的剪生货的 =+3+ =002 得到min二=+名+名 1-0 420200mm- 月理。乙的混合策路求解的线性提划模型为 因此原收益纯阵如上4可变为 =++ 6,+9y≤1 1=005 -别 14 2 2 3 5 7 11 0 1 例3：求解下面零和博弈矩阵的混合策略        7 5 2 2 3 11 A 解：设甲的混合策略为 (x,1 x) , x[0,1] 则 X*         2 5 9 2 V x V x G G      49 /11 3/11 VG x 根据图可分析出，乙不可能选择策略1，因此y1=0           2 3 1 49 /11 5 2 49 /11 3 11 2 3 2 3 y y y y y y      2 /11 9 /11 3 2 y y 因此，该博弈中，甲的混合策略为 乙的混合策略为 ) 11 8 , 11 3 ( * x  ) 11 2 , 11 9 (0, * y  最优期望收益为 11 49 VG  练习：求解下面零和博弈矩阵的混合策略          2 6 7 11 6 2 A 解：设乙的混合策略为 ( y,1 y) , y [0,1] 2 2 6 6 7 11 B1 B2 ] 9 4 , 5 1 ( ,1 ), [ * y  y  y 其中y  (0,1,0) * x   6 VG 线性规划解法 求解零和博弈 ，其中 { , ; } G  S1 S2 A { , , }, { , , } S1  1 2 3 S2  1 2 3             5 1 4 2 0 3 4 2 5 A 解：设参与人甲的最优混合策略为 ，期望收益为 ， 则得到如下一组不等式   1 2 3 p , p , p v              p a p a p a v p a p a p a v p a p a p a v 1 13 2 23 3 33 1 12 2 22 3 32 1 11 2 21 3 31 令 v v p p p x x x v p x v p x v p x 1 , , , 1 2 3 1 2 3 3 3 2 2 1 1       则    得到                     0, 0, 0 1 1 1 1 min 1 2 3 1 13 2 23 3 33 1 12 2 22 3 32 1 11 2 21 3 31 1 2 3 x x x x a x a x a x a x a x a x a x a x a x x x v 甲希望期望收益 最大化，则应将 最小化 v 1 2 3 1 x x x v    根据收益矩阵情况，所有元素可加上适当的数使得v非负， 这样，线性规划模型的变量取值即可要求全为非负，即 因此原收益矩阵加上4可变为          9 3 0 6 4 7 0 6 9 A'                   0, 0, 0 9 7 1 6 4 3 1 6 9 1 1 min 1 2 3 1 2 1 2 3 2 3 1 2 3 x x x x x x x x x x x x x v 代入甲的线性规划模型，得到            9 1 2 min 0.0542 0.0854 0.0826 3 2 1 v x x x        0.244 0.384 0.372 3 2 1 p p p 同理，乙的混合策略求解的线性规划模型为                   0, 0, 0 9 3 1 6 4 7 1 6 9 1 1 max 1 2 3 1 2 1 2 3 2 3 1 2 3 y y y y y y y y y y y y y v            9 1 2 max 0 0.1667 0.0556 3 2 1 v y y y        0 0.75 0.25 3 2 1 q q q