
第之节 第八章 空冈曲线及其方程 空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影
第八章 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影 第六节 空间曲线及其方程

一、空间曲线的一般方程 空间曲线可视为两曲面的交线,其一般方程为方程组 F(x,y,z)=0 S2 G(x,y,z)=0 例如,方程组 G(x,y,z)=0F(x,y,z)=0 x2+y2=1 2x+3z=6 表示圆柱面与平面的交线C
一、空间曲线的一般方程 空间曲线可视为两曲面的交线, 其一般方程为方程组 S2 L 1 S 例如,方程组 表示圆柱面与平面的交线 C. x z 1 y o C 2
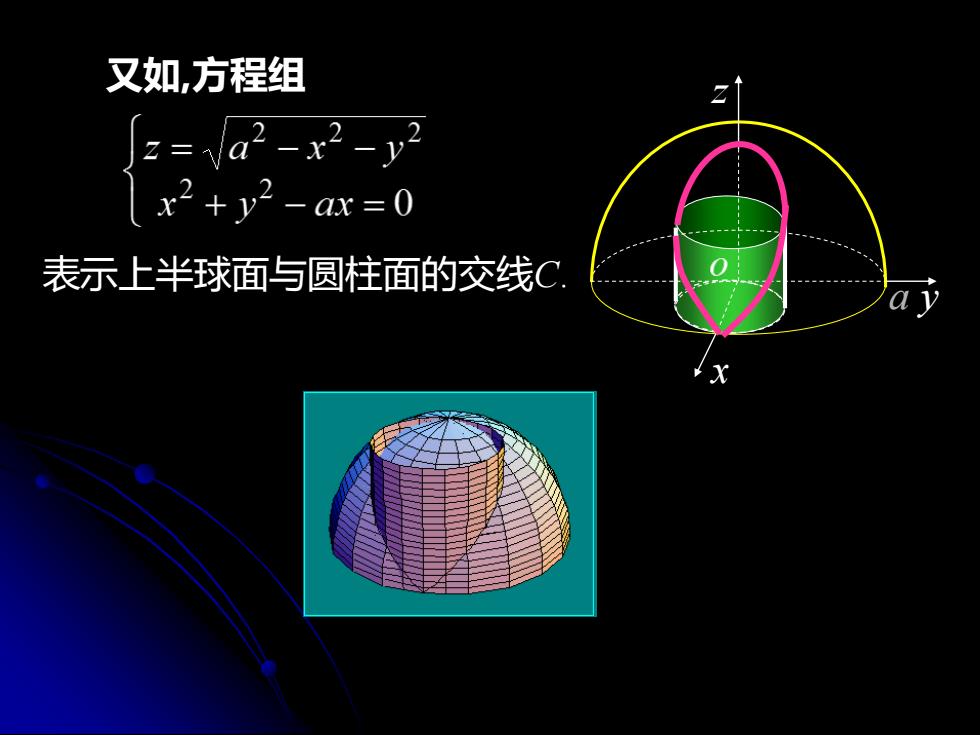
又如,方程组 2=a2-x2-y x2+y2-ax=0 表示上半球面与圆柱面的交线C
又如,方程组 表示上半球面与圆柱面的交线C. y x z a

二、空间曲线的参数方程 将曲线C上的动点坐标x,y,z表示成参数t的函数: x=x(t) y(t) z(t) 称它为空间曲线的参数方程
二、空间曲线的参数方程 将曲线C上的动点坐标x, y, z表示成参数t 的函数: 称它为空间曲线的参数方程
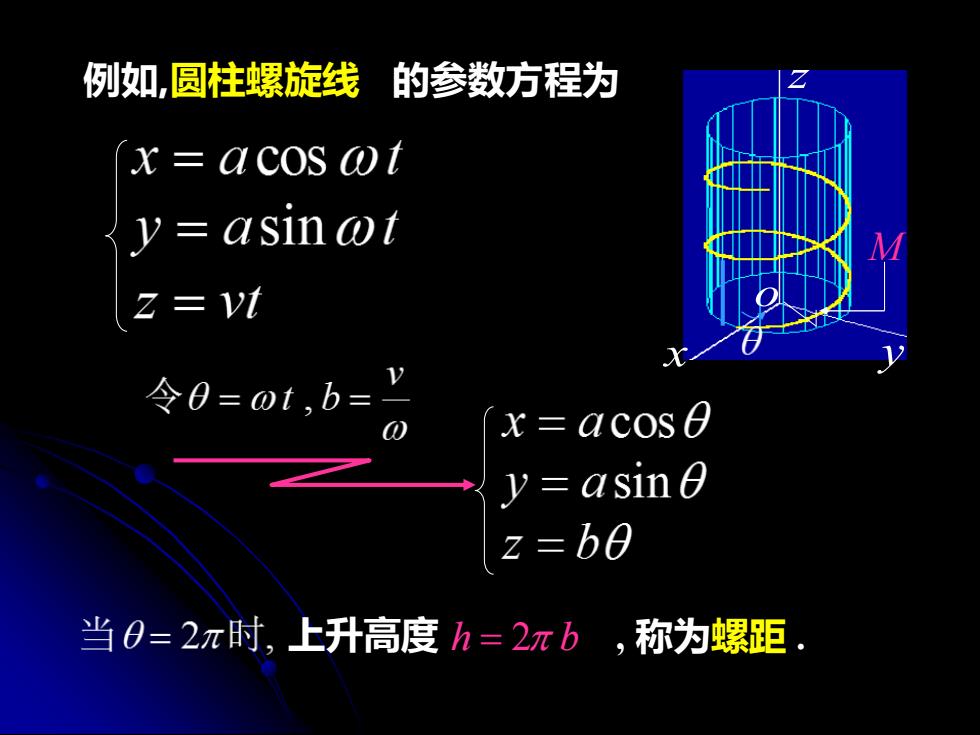
例如圆柱螺旋线 的参数方程为 x=acos ot Z=V 令0=0t,b= 0 [x acos0 y=asin z=b0 当0=2π时,上升高度h=2πb,称为螺距
z x y o 例如,圆柱螺旋线 h = 2 b 的参数方程为 上升高度 , 称为螺距 . M

例1.将下列曲线化为参数方程表示: x2+y2=1 (2) =/a2-x2-y 2x+3z=6 x2+y2-ax=0 解:(1) 根据第一方程引入参数,得所求为 x=coSt y=sint (0≤t≤2π) z=3(6-2c0st) 2)将第二方程变形为(x-)2+y2=,故所求为 (x=号+号cost y=号sint (0≤t≤2π) Z=a、 coSt
例1. 将下列曲线化为参数方程表示: 解: (1) 根据第一方程引入参数 , (2) 将第二方程变形为 故所求为 得所求为

注:曲面的参数方程 球面的参数方程为 x =asing cose y=asino sin 0≤0≤π 0≤0≤2π z=acoso 说明:一般曲面的参数方程含两个参数,形如 x=x(s,t) y=y(s,t) z=z(s,t)
球面 的参数方程为 注:曲面的参数方程 说明: 一般曲面的参数方程含两个参数 , 形如

三、空间曲线在坐标面上的投影 设空间曲线C的一般方程为 F(x,y,z)=0 1G(x,y,2)=0 消去z得投影柱面 H(x,y)=0, 则C在xoy面上的投影曲线C为 H(x,y)=0 Z=0
三、空间曲线在坐标面上的投影 设空间曲线 C 的一般方程为 消去 z 得投影柱面 则C 在xoy 面上的投影曲线 C´为 = = 0 ( , ) 0 z H x y z y x C C

消去x得C在v0z面上的投影曲线方程 R(y,z)=0 x=0 消去y得C在zox面上的投影曲线方程 T(x,z)=0 y=0
消去 x 得C 在yoz 面上的投影曲线方程 消去y 得C 在zox 面上的投影曲线方程 = = 0 ( , ) 0 x R y z = = 0 ( , ) 0 y T x z

例如 +z2=1 +(y-1)2+(z-1)2=1 在xoy面上的投影曲线方程为 x2+2y2-2y=0 z=0
z y x C 1 o 例如 在xoy 面上的投影曲线方程为 = + − = 0 2 2 0 2 2 z x y y