
第一讲多元丞数的基本概念
第一讲 多元函数的基本概念

多元函数的基本概念 一、多元函数的概念 二、多元数的极限 三、多元函数的连续性
多元函数的基本概念 一、多元函数的概念 二、多元函数的极限 三、多元函数的连续性

多元函数的基本概念 一、多元函数的概念 二、多元函数的极限 三、多元数的连续性
多元函数的基本概念 一、多元函数的概念 二、多元函数的极限 三、多元函数的连续性

多元函数的概念 (一) 3引例 (二)平面点集 (三)多元函数的定义
一、多元函数的概念 (一)引例 (二)平面点集 (三)多元函数的定义

一、多元函数的概念 (一)3引例 (二) 平面点集 (三)多元函数的定义
一、多元函数的概念 (一)引例 (二)平面点集 (三)多元函数的定义

(一)引例 ◆例1圆柱体的体积 底面半径:r 高: 二元函数 →V=πr27i ◆例2三角形的面积 (1)三边长:a,b,c 三元函数 =S=p/(p-a)(p-b)(p-c) P=。(a+b+c)(海伦公式) 2 (2)两边长:4,b中品一 7 三元函数 S=二absinC(正弦定理) 2
(一)引例 圆柱体的体积 r h 三角形的面积 a b c ◆例1 V r h 2 = 底面半径: r 高: h ◆例2 三边长: a,b,c S = p ( p − a)( p − b)( p − c) ( ) 2 1 p = a + b + c (海伦公式) 两边长: a,b 夹角: C (1) (2) S absinC 2 1 = (正弦定理) C 二元函数 三元函数 三元函数

一、多元函数的概念 (一)引例 (二) 平面点集 (三)多元函数的定义
一、多元函数的概念 (一)引例 (二)平面点集 (三)多元函数的定义

、多元函数的概念 (一)31例 (二)平面点集 (三)多元函数的定义
一、多元函数的概念 (一)引例 (二)平面点集 (三)多元函数的定义
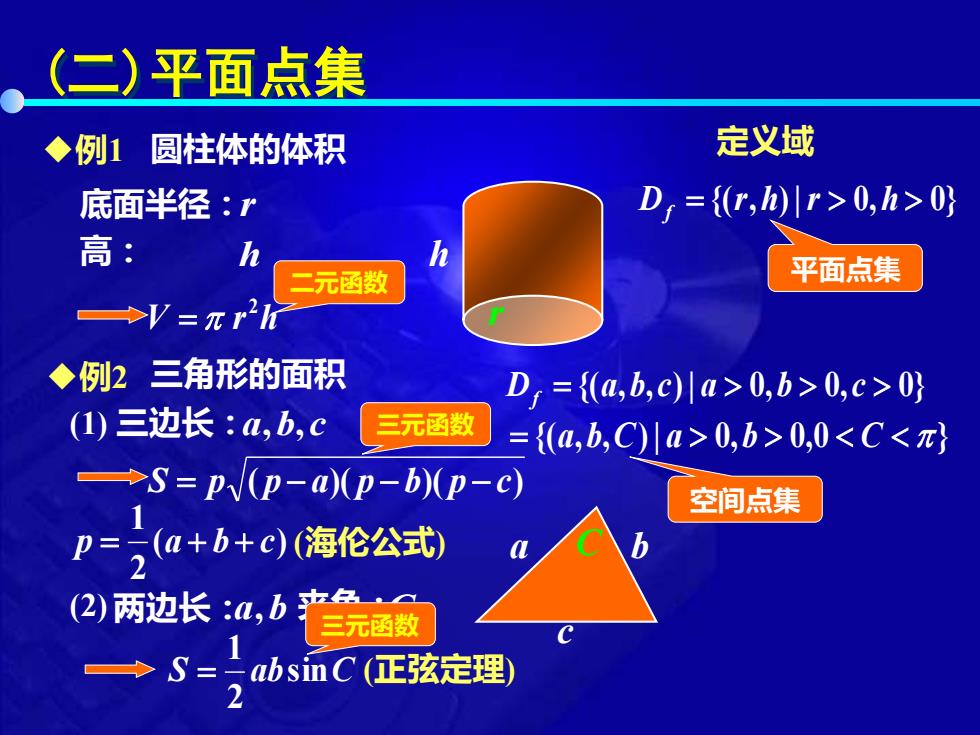
(二)平面点集 ◆例1圆柱体的体积 定义域 底面半径:r D,={r,)lr>0,h>0 高: 二元函数 平面点集 →V=元r2 ◆例2三角形的面积 D,={(a,b,c)川a>0,b>0,c>0} (1)三边长:a,b,c 三元函数 ={(a,b,C)川a>0,b>0,0<C<π →S=p√(p-@(p-b(p-C) 空间点集 P=2a+b+c海伦公试) (2)两边长:4,b色☑ 三元函数 S=二absinC正弦定理) 2
(二)平面点集 圆柱体的体积 r h 三角形的面积 a b c ◆例1 V r h 2 = 底面半径: r 高: h ◆例2 三边长: a,b,c S = p ( p − a)( p − b)( p − c) ( ) 2 1 p = a + b + c (海伦公式) 两边长: a,b 夹角: C (1) (2) S absinC 2 1 = (正弦定理) C 定义域 D = {(r,h)|r 0,h 0} f D = {(a,b,c)| a 0,b 0,c 0} f = {(a,b,C)| a 0,b 0,0 C } 平面点集 空间点集 二元函数 三元函数 三元函数

>平面点集的有关概念 二维空间: 二元有序实数组(ky)的全体,即:{(x,y)川x∈R,y∈R 记作:R或RxR ●注 (1)二维空间的几何意义一坐标平面 (2)二维空间的元素一P=(x,y) 坐标平面内的点 平面点集: 二维空间的任一子集,记作:ECR ●注 平面点集通常是坐标平面上具有某种性质的点的集合, 记作E={化,y)(,y)具有性质P
➢平面点集的有关概念 二维空间: 二元有序实数组(x,y)的全体, 即: 记作: ⚫注 二维空间的几何意义—坐标平面 二维空间的元素— P x y = ( , ) 坐标平面内的点 平面点集: 二维空间的任一子集, 记作: 平面点集E通常是坐标平面上具有某种性质的点的集合, 记作:E={(x,y)|(x,y)具有性质P} (1) (2) {( x, y)| x R, y R} 2 E R ⚫注 或 R R 2 R