
Chapter 14:Query Optimization Introduction Transformation of Relational Expressions Catalog Information for Cost Estimation Statistical Information for Cost Estimation Cost-based optimization Dynamic Programming for Choosing Evaluation Plans Materialized views Database System Concepts-5th Edition,Oct 5,2006. 14.2 @Silberschatz,Korth and Sudarshan
Database System Concepts - 5 14.2 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Chapter 14: Query Optimization Introduction Transformation of Relational Expressions Catalog Information for Cost Estimation Statistical Information for Cost Estimation Cost-based optimization Dynamic Programming for Choosing Evaluation Plans Materialized views
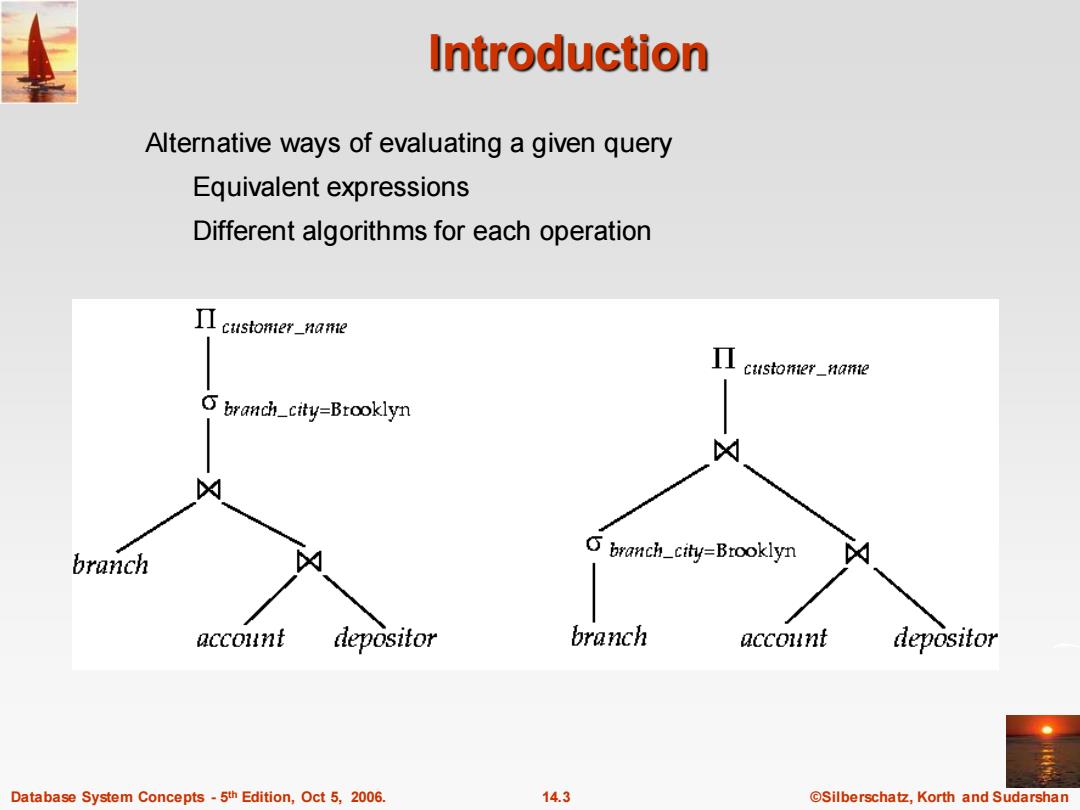
Introduction Alternative ways of evaluating a given query Equivalent expressions Different algorithms for each operation Π customer_nane Π customer._行afie branch_city=Brooklyn branch branch_city=Brooklyn account depositor branch account depositor Database System Concepts-5th Edition,Oct 5,2006. 14.3 @Silberschatz,Korth and Sudarshan
Database System Concepts - 5 14.3 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Introduction Alternative ways of evaluating a given query Equivalent expressions Different algorithms for each operation
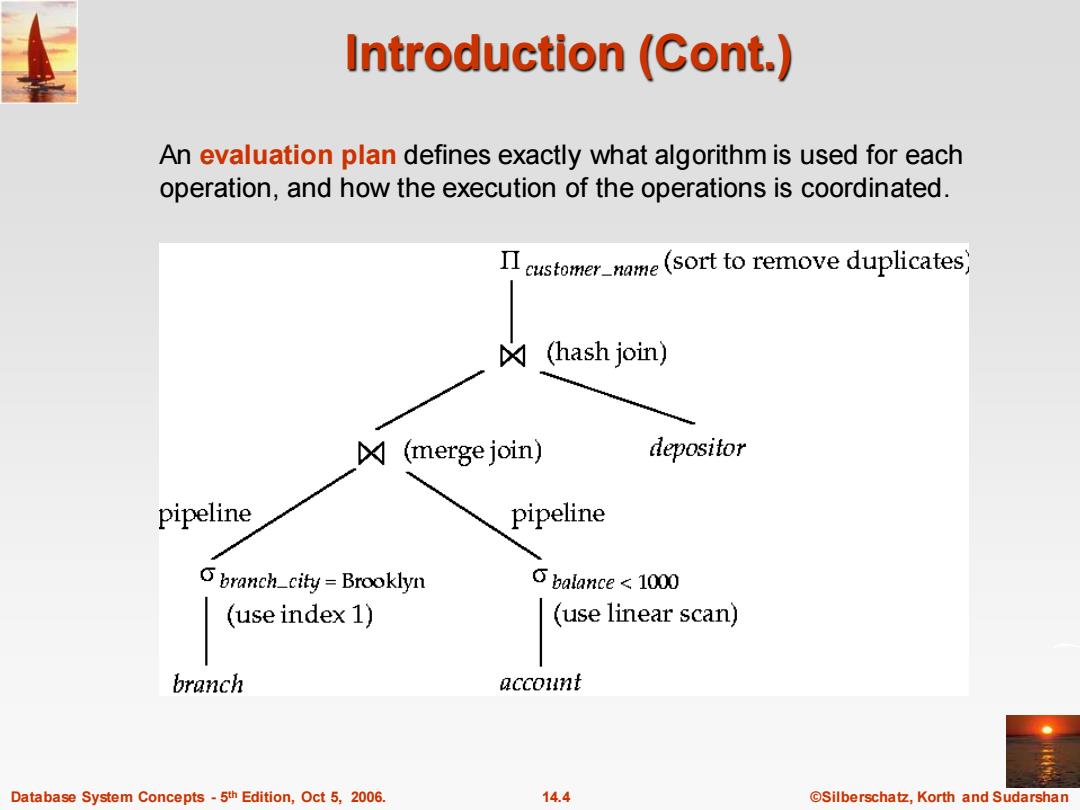
Introduction (Cont.) An evaluation plan defines exactly what algorithm is used for each operation,and how the execution of the operations is coordinated. Π customer_name(sort to remove duplicates) ☆(hash join) ☒(merge join) depositor pipeline pipeline branch_city Brooklyn balance<1000 (use index 1) (use linear scan) branch account Database System Concepts-5th Edition,Oct 5,2006. 14.4 ©Silberschat乜,Korth and Sudarshan
Database System Concepts - 5 14.4 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Introduction (Cont.) An evaluation plan defines exactly what algorithm is used for each operation, and how the execution of the operations is coordinated

Introduction (Cont.) Cost difference between evaluation plans for a query can be enormous E.g.seconds vs.days in some cases Steps in cost-based query optimization 1.Generate logically equivalent expressions using equivalence rules 2.Annotate resultant expressions to get alternative query plans 3.Choose the cheapest plan based on estimated cost Estimation of plan cost based on: Statistical information about relations.Examples: number of tuples,number of distinct values for an attribute Statistics estimation for intermediate results to compute cost of complex expressions Cost formulae for algorithms,computed using statistics Database System Concepts-5th Edition,Oct 5,2006. 14.5 @Silberschatz,Korth and Sudarshan
Database System Concepts - 5 14.5 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Introduction (Cont.) Cost difference between evaluation plans for a query can be enormous E.g. seconds vs. days in some cases Steps in cost-based query optimization 1. Generate logically equivalent expressions using equivalence rules 2. Annotate resultant expressions to get alternative query plans 3. Choose the cheapest plan based on estimated cost Estimation of plan cost based on: Statistical information about relations. Examples: number of tuples, number of distinct values for an attribute Statistics estimation for intermediate results to compute cost of complex expressions Cost formulae for algorithms, computed using statistics

☒ 无法显示该图片。 Generating Equivalent Expressions Database System Concepts 5th Ed. @Silberschatz,Korth and Sudarshan See www.db-book.com for conditions on re-use
Database System Concepts 5th Ed. ©Silberschatz, Korth and Sudarshan See www.db-book.com for conditions on re-use Generating Equivalent Expressions

Transformation of Relational Expressions Two relational algebra expressions are said to be equivalent if the two expressions generate the same set of tuples on every legal database instance Note:order of tuples is irrelevant In SQL,inputs and outputs are multisets of tuples Two expressions in the multiset version of the relational algebra are said to be equivalent if the two expressions generate the same multiset of tuples on every legal database instance. An equivalence rule says that expressions of two forms are equivalent Can replace expression of first form by second,or vice versa Database System Concepts-5th Edition,Oct 5,2006. 14.7 @Silberschatz,Korth and Sudarshan
Database System Concepts - 5 14.7 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Transformation of Relational Expressions Two relational algebra expressions are said to be equivalent if the two expressions generate the same set of tuples on every legal database instance Note: order of tuples is irrelevant In SQL, inputs and outputs are multisets of tuples Two expressions in the multiset version of the relational algebra are said to be equivalent if the two expressions generate the same multiset of tuples on every legal database instance. An equivalence rule says that expressions of two forms are equivalent Can replace expression of first form by second, or vice versa

Equivalence Rules 1.Conjunctive selection operations can be deconstructed into a sequence of individual selections. eno,(E)=Oo(Oo,(E)) 2.Selection operations are commutative. 06(o4,(E)=o6,(o6(E)》 3.Only the last in a sequence of projection operations is needed,the others can be omitted. Πz(Π,(.(Πn(E).…》=Π(E) 4. Selections can be combined with Cartesian products and theta joins. ao(E1XE2)=E1☒9E2 b.o01(E1凶2E2)=E1凶91A92E2 Database System Concepts-5th Edition,Oct 5,2006. 14.8 ©Silberschat乜,Korth and Sudarshan
Database System Concepts - 5 14.8 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Equivalence Rules 1. Conjunctive selection operations can be deconstructed into a sequence of individual selections. 2. Selection operations are commutative. 3. Only the last in a sequence of projection operations is needed, the others can be omitted. 4. Selections can be combined with Cartesian products and theta joins. a. (E1X E2 ) = E1 E2 b. 1 (E1 2 E2 ) = E1 1 2 E2 ( ( )) ( ( )) 1 2 2 1 E = E ( ) ( ( )) 1 2 1 2 E = E ( ( ( ( )) )) ( ) 1 2 1 L L Ln E = L E

Equivalence Rules (Cont.) 5.Theta-join operations(and natural joins)are commutative. E1凶gE2=E2☒gE1 6.(a)Natural join operations are associative: (E凶E2)凶E3=E凶(E2E3) (b)Theta joins are associative in the following manner: (E1凶91E2)☒203E3=E1☒01A93(E2凶2E3) where 02 involves attributes from only E2 and E3. Database System Concepts-5th Edition,Oct 5,2006. 14.9 @Silberschatz,Korth and Sudarshan
Database System Concepts - 5 14.9 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Equivalence Rules (Cont.) 5. Theta-join operations (and natural joins) are commutative. E1 E2 = E2 E1 6. (a) Natural join operations are associative: (E1 E2 ) E3 = E1 (E2 E3 ) (b) Theta joins are associative in the following manner: (E1 1 E2 ) 2 3 E3 = E1 1 3 (E2 2 E3 ) where 2 involves attributes from only E2 and E3
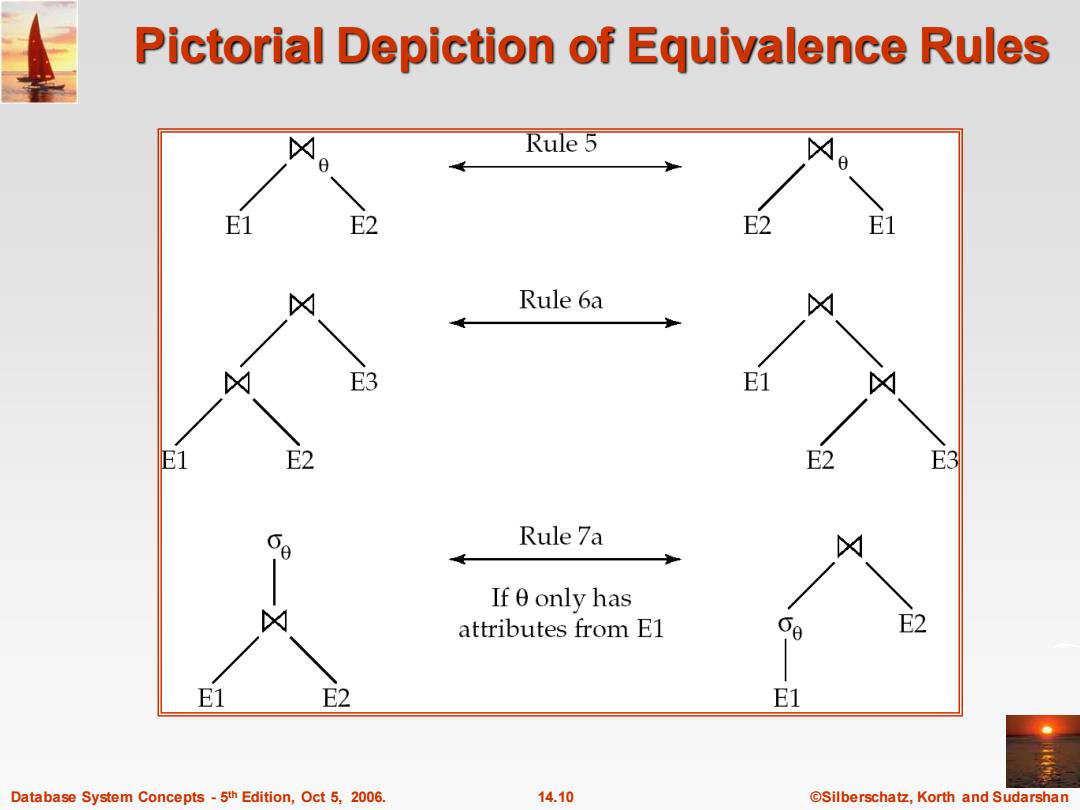
Pictorial Depiction of Equivalence Rules Rule 5 E1 E2 E2 E1 Rule 6a ☒ E3 E1 E1 E2 E2 E3 68 Rule 7a If 0 only has ☒ attributes from El 60 E2 E1 E2 E1 Database System Concepts-5th Edition,Oct 5,2006. 14.10 @Silberschatz,Korth and Sudarshan
Database System Concepts - 5 14.10 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Pictorial Depiction of Equivalence Rules

Equivalence Rules (Cont.) 7.The selection operation distributes over the theta join operation under the following two conditions: (a)When all the attributes in 0o involve only the attributes of one of the expressions (E1)being joined. 0(E1E2)=(o0(E1)凶gE2 (b)When 0 1 involves only the attributes of E1 and 02 involves only the attributes of E2. o1N2(E1凶E2)=(o1(E1)Xg(o2(E2) Database System Concepts-5th Edition,Oct 5,2006. 14.11 ©Silberschat乜,Korth and Sudarshan
Database System Concepts - 5 14.11 ©Silberschatz, Korth and Sudarshan th Edition, Oct 5, 2006. Equivalence Rules (Cont.) 7. The selection operation distributes over the theta join operation under the following two conditions: (a) When all the attributes in 0 involve only the attributes of one of the expressions (E1 ) being joined. 0 (E1 E2 ) = (0 (E1 )) E2 (b) When 1 involves only the attributes of E1 and 2 involves only the attributes of E2 . 1 (E1 E2 ) = (1 (E1 )) ( (E2 ))