
电子斜技大学 软件技术基础 3.5.3二叉树的操作 主讲教师:刘民岷 航空航天学院 a■ 软件技术基础课程组
软件技术基础 主讲教师:刘民岷 航空航天学院 软件技术基础课程组
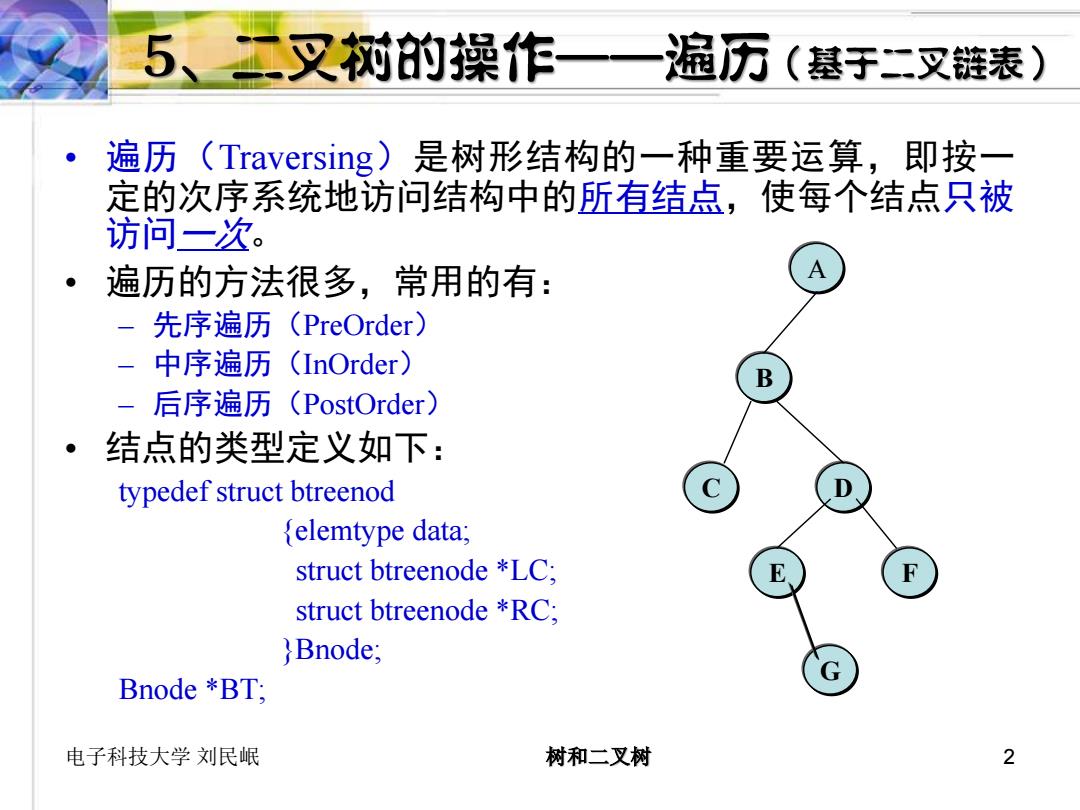
5、二叉树的操作一一 遍历 (基于二叉链表) 遍历(Traversing)是树形结构的一种重要运算,即按一 定的次序系统地访问结构中的所有结点,使每个结点只被 访问一次。 遍历的方法很多,常用的有: 先序遍历(PreOrder). 中序遍历(InOrder) B - 后序遍历(PostOrder) 结点的类型定义如下: typedef struct btreenod D elemtype data; struct btreenode *LC: E F struct btreenode *RC: Bnode; G Bnode *BT: 电子科技大学刘民岷 树和二叉树 2
电子科技大学 刘民岷 树和二叉树 2 • 遍历(Traversing)是树形结构的一种重要运算,即按一 定的次序系统地访问结构中的所有结点,使每个结点只被 访问一次。 • 遍历的方法很多,常用的有: – 先序遍历(PreOrder) – 中序遍历(InOrder) – 后序遍历(PostOrder) • 结点的类型定义如下: typedef struct btreenod {elemtype data; struct btreenode *LC; struct btreenode *RC; }Bnode; Bnode *BT; A B C D E F G
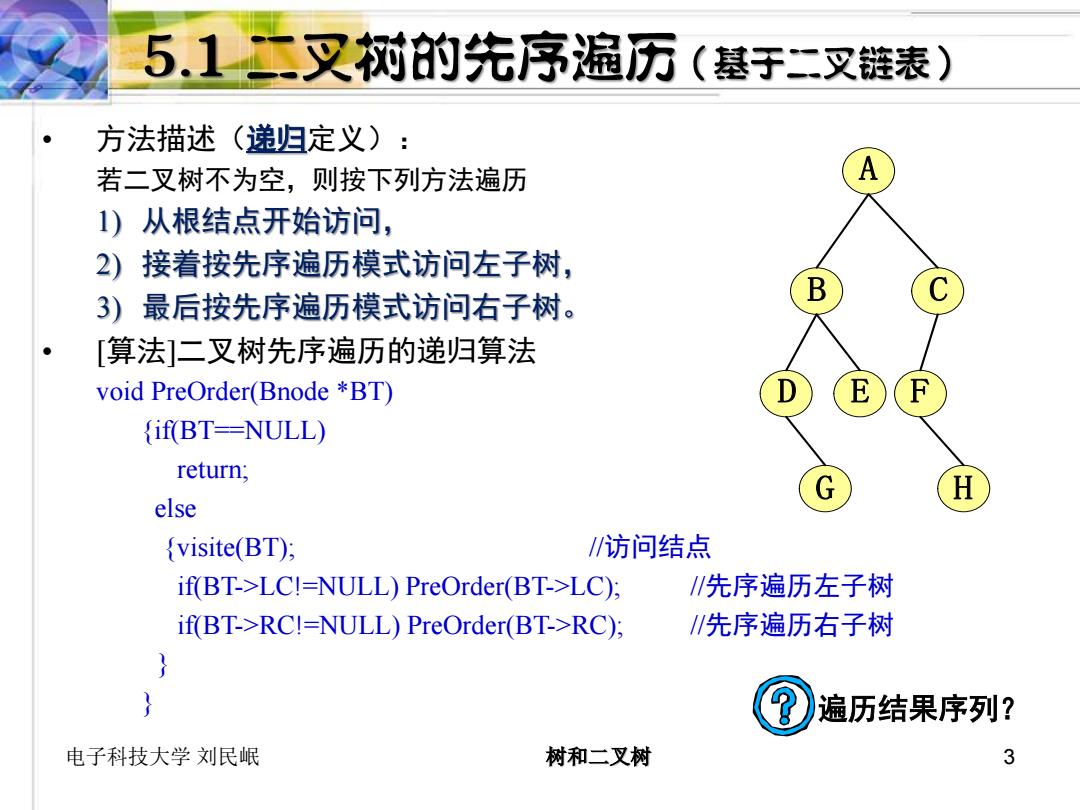
5.1二叉对的先序遍历 (基于二叉链表) 方法描述(递归定义): 若二叉树不为空,则按下列方法遍历 A 1)从根结点开始访问, 2)接着按先序遍历模式访问左子树, ( 3)最后按先序遍历模式访问右子树。 B [算法]二叉树先序遍历的递归算法 void PreOrder(Bnode *BT) E if(BT=NULL) return; H else visite(BT); /访问结点 if(BT->LC!=NULL)PreOrder(BT->LC): /先序遍历左子树 if(BT->RC!=NULL)PreOrder(BT->RC); /先序遍历右子树 遍历结果序列? 电子科技大学刘民岷 树和二叉树 3
电子科技大学 刘民岷 树和二叉树 3 • 方法描述(递归定义): 若二叉树不为空,则按下列方法遍历 1) 从根结点开始访问, 2) 接着按先序遍历模式访问左子树, 3) 最后按先序遍历模式访问右子树。 • [算法]二叉树先序遍历的递归算法 void PreOrder(Bnode *BT) {if(BT==NULL) return; else {visite(BT); //访问结点 if(BT->LC!=NULL) PreOrder(BT->LC); //先序遍历左子树 if(BT->RC!=NULL) PreOrder(BT->RC); //先序遍历右子树 } } A B C D E F G H 遍历结果序列?
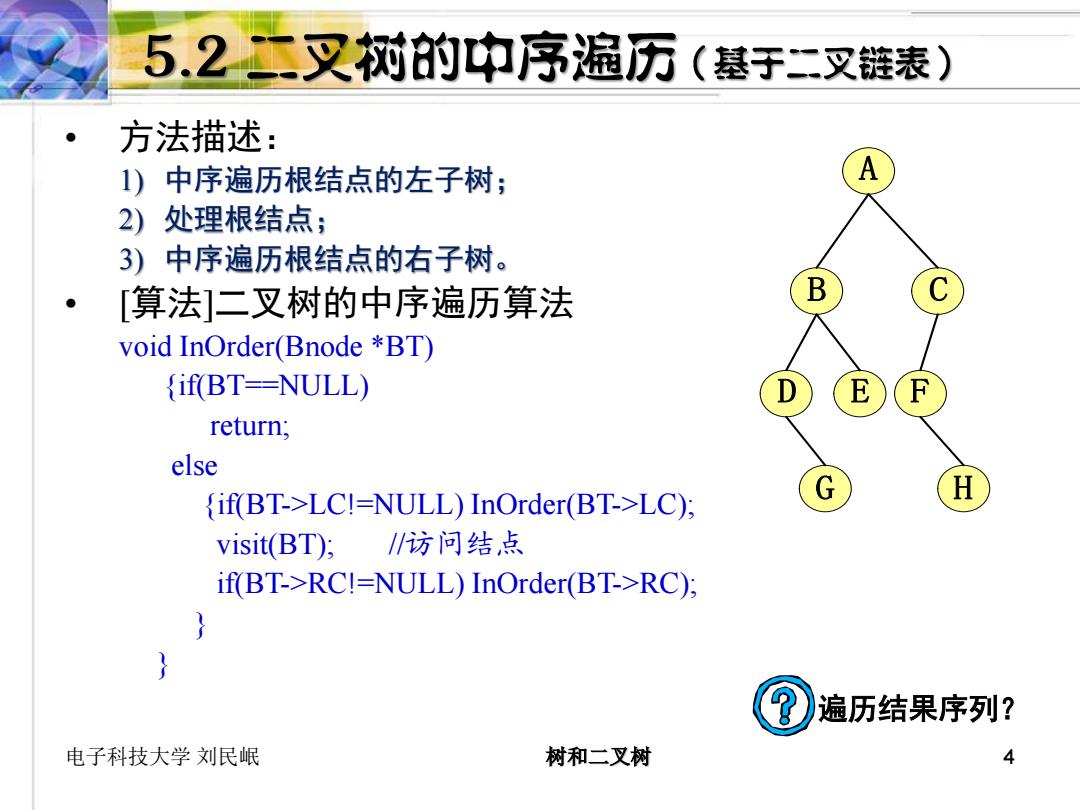
5.2二叉树的中序遍历(基于二叉链表) 方法描述: 1)中序遍历根结点的左子树; A 2)处理根结点; 3)中序遍历根结点的右子树。 [算法]二叉树的中序遍历算法 B void InOrder(Bnode *BT) if(BT==NULL) E return; else G if(BT->LC!=NULL)InOrder(BT->LC): H visit(BT); /访问结,点 if(BT->RC!=NULL)InOrder(BT->RC): 遍历结果序列? 电子科技大学刘民岷 树和二叉树 4
电子科技大学 刘民岷 树和二叉树 4 A B C D E F G H • 方法描述: 1) 中序遍历根结点的左子树; 2) 处理根结点; 3) 中序遍历根结点的右子树。 • [算法]二叉树的中序遍历算法 void InOrder(Bnode *BT) {if(BT==NULL) return; else {if(BT->LC!=NULL) InOrder(BT->LC); visit(BT); //访问结点 if(BT->RC!=NULL) InOrder(BT->RC); } } 遍历结果序列?
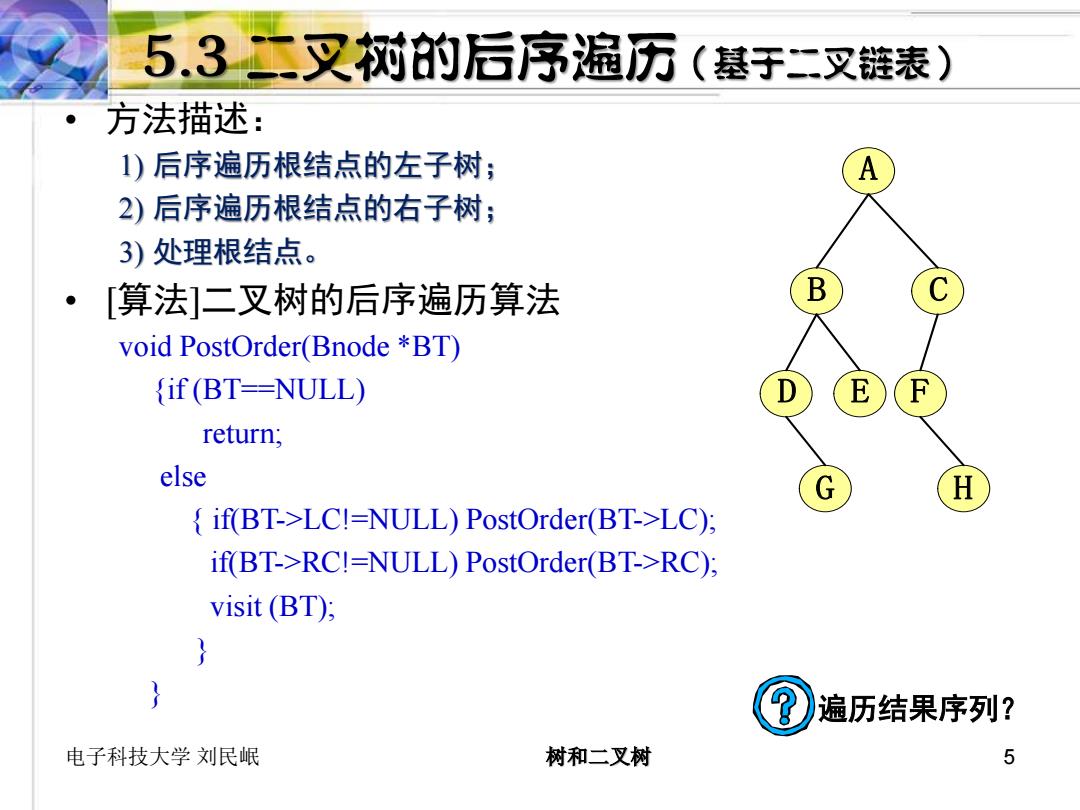
5.3二叉树的后序遍历(基于二叉链表) 方法描述 )后序遍历根结点的左子树; A 2)后序遍历根结点的右子树; 3)处理根结点。 「算法]二叉树的后序遍历算法 B void PostOrder(Bnode *BT) if(BT-=NULL) E return; else G H if(BT->LC!=NULL)PostOrder(BT->LC): if(BT->RC!=NULL)PostOrder(BT->RC): visit(BT): 遍历结果序列? 电子科技大学刘民岷 树和二叉树 5
电子科技大学 刘民岷 树和二叉树 5 A B C D E F G H 遍历结果序列? • 方法描述: 1) 后序遍历根结点的左子树; 2) 后序遍历根结点的右子树; 3) 处理根结点。 • [算法]二叉树的后序遍历算法 void PostOrder(Bnode *BT) {if (BT==NULL) return; else { if(BT->LC!=NULL) PostOrder(BT->LC); if(BT->RC!=NULL) PostOrder(BT->RC); visit (BT); } }

、二叉树的重构 根据中序遍历序列加先序遍历序列(或后序遍历序列)可以 重构二叉树 以中序序列加后序序列为例,构造步骤如下: (中序遍历(左一根一右);后序遍历(左一右一根)) -从后序序列中取出最后一个结点(二叉树的根); 根据这个根结点在中序序列中将树分为左右两棵子树; -分别对左右子树重复上面两步。 ·例:已知一二叉树中序序列为CBDEAFHIGJ,.后序序列为CEDBIHJGFA,试 构造这棵二叉树。 电子科技大学刘民岷 树和二叉树 6
电子科技大学 刘民岷 树和二叉树 6 • 根据中序遍历序列加先序遍历序列(或后序遍历序列)可以 重构二叉树 • 以中序序列加后序序列为例,构造步骤如下: (中序遍历(左-根-右);后序遍历(左-右-根)) –从后序序列中取出最后一个结点(二叉树的根); –根据这个根结点在中序序列中将树分为左右两棵子树; –分别对左右子树重复上面两步。 • 例:已知一二叉树中序序列为CBDEAFHIGJ,后序序列为CEDBIHJGFA,试 构造这棵二叉树

7、二叉挑序树的生成 二叉排序树的中序序列是一个递增的有序序列 ● 二叉排序树的生成步骤:已知一序列k,k2,,k} 一K作为二叉树的根; 若k2=k?且k右 子树空,则将k插入到k的右子树。 ·[例]已知序列 [190,381,12,40,410,394,540,760,85,476,800,146,9,445,600},试 构造一棵二叉排序树。 电子科技大学刘民岷 树和二叉树 7
电子科技大学 刘民岷 树和二叉树 7 • 二叉排序树的中序序列是一个递增的有序序列 • 二叉排序树的生成步骤:已知一序列{k1,k2,…,kn} – K1作为二叉树的根; – 若k2=kj,且kj右 子树空,则将ki插入到kj的右子树。 • [例]已知序列 {190,381,12,40,410,394,540,760,85,476,800,146,9,445,600},试 构造一棵二叉排序树

7、二叉排序树的生成(续) [例们已知序列 {190,381,12,40,410,394,540,760,85,476,800,146,9,445,600},试 构造一棵二叉排序树。 电子科技大学刘民岷 树和二叉树 8
电子科技大学 刘民岷 树和二叉树 8 • [例]已知序列 {190,381,12,40,410,394,540,760,85,476,800,146,9,445,600},试 构造一棵二叉排序树
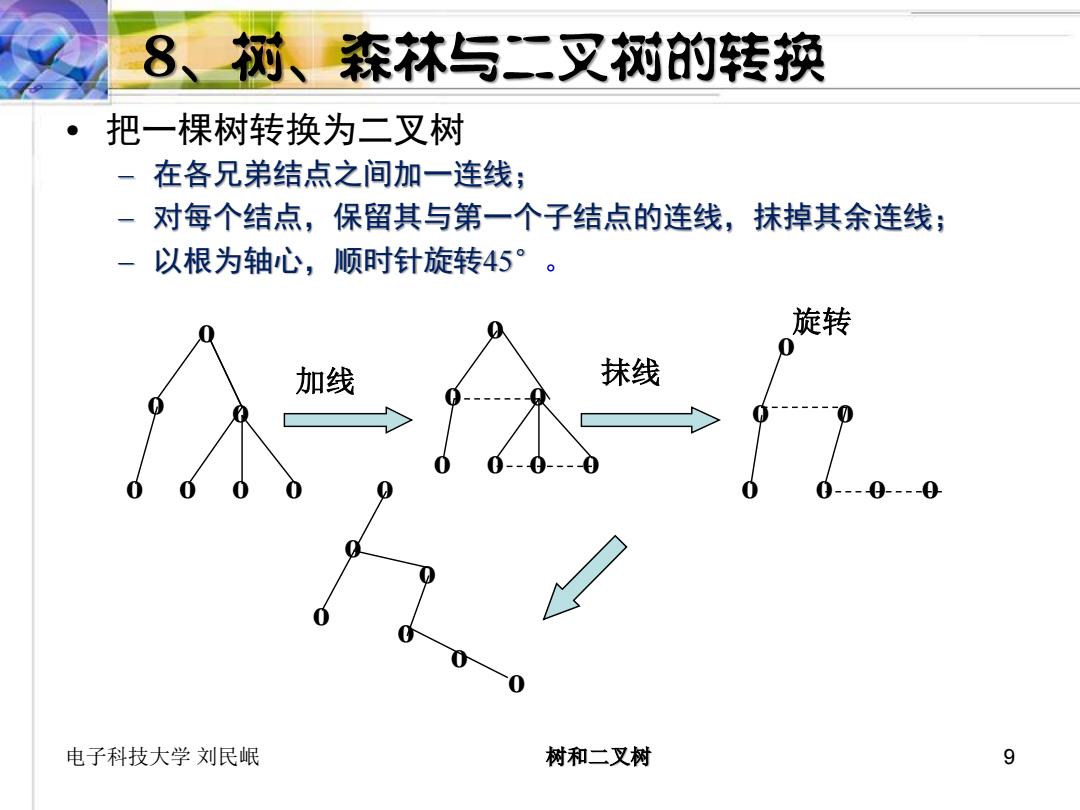
8、树、森林与二叉树的转换 把一棵树转换为二叉树 一在各兄弟结点之间加一连线; 对每个结点,保留其与第一个子结点的连线,抹掉其余连线; 以根为轴心,顺时针旋转45°。 旋转 加线 抹线 0- 电子科技大学刘民岷 树和二叉树 9
电子科技大学 刘民岷 树和二叉树 9 • 把一棵树转换为二叉树 – 在各兄弟结点之间加一连线; – 对每个结点,保留其与第一个子结点的连线,抹掉其余连线; – 以根为轴心,顺时针旋转45° 。 o o o o o o o o o o o o o o 加线 抹线 o o o o o o o 旋转 o o o o o o o

8、树、森林与二叉树的转换(续) 森林转换为相应的二叉树 一将每棵树转换成对应的二叉树; 一将森林中每棵树的树根连接起来; 以森林中第一棵树的根为轴顺时针旋转一个角度。 连线 抹线 旋转 电子科技大学刘民岷 树和二叉树 10
电子科技大学 刘民岷 树和二叉树 10 • 森林转换为相应的二叉树 – 将每棵树转换成对应的二叉树; – 将森林中每棵树的树根连接起来; – 以森林中第一棵树的根为轴顺时针旋转一个角度。 o o o o o o o o o o 连线 o o o o o o o o o o 抹线 o o o o o o o o o o 旋转 o o o o o o o o o o