
电子斜技大学 软件技术基础 3.6.2图的物理存储 主讲教师:刘民岷 航空航天学院 a■ 软件技术基础课程组
软件技术基础 主讲教师:刘民岷 航空航天学院 软件技术基础课程组

2、图的物理存储 前面在讨论树和线性表的存储结构时,用到两种存储结 构:顺序表和链表。 实际上,在图的存储涉及到顶点的存储和边的存储。顶 点可以使用数组进行存储,边则常用下面两种方法存储: ·邻接矩阵 邻接表 电子科技大学刘民岷 图 2
电子科技大学 刘民岷 图 2 前面在讨论树和线性表的存储结构时,用到两种存储结 构:顺序表和链表。 实际上,在图的存储涉及到顶点的存储和边的存储。顶 点可以使用数组进行存储,边则常用下面两种方法存储: • 邻接矩阵 • 邻接表
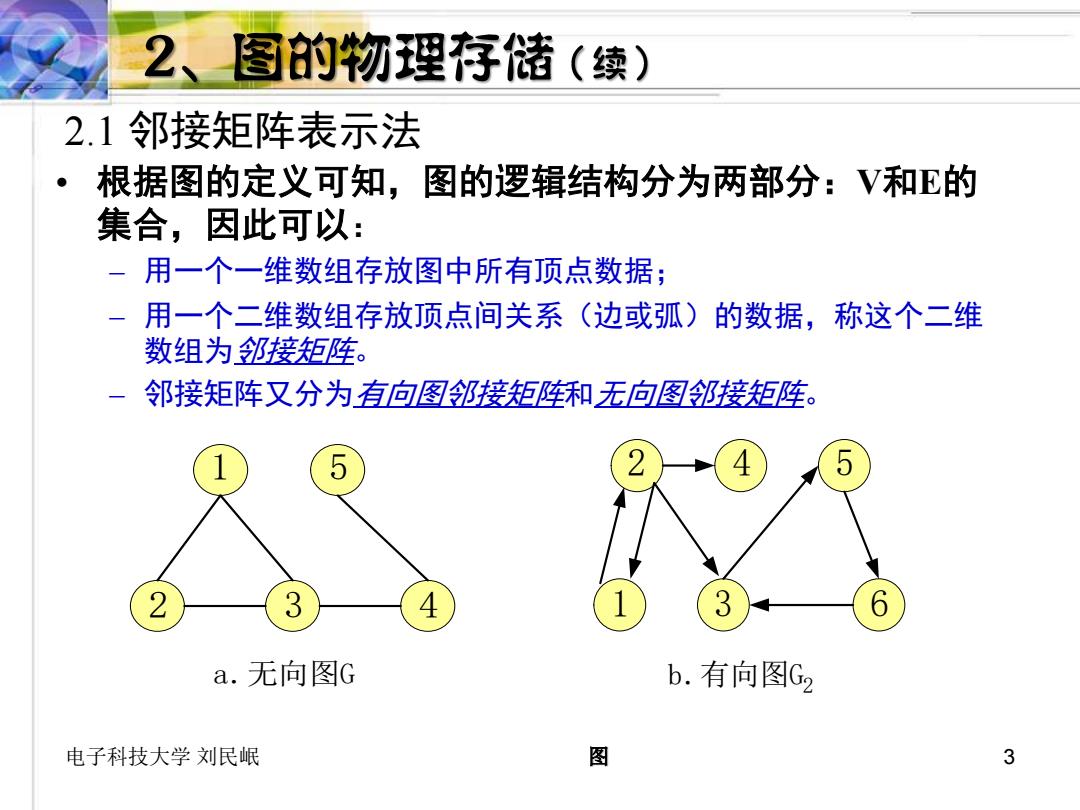
2、图的物理存储(续) 2.1邻接矩阵表示法 。 根据图的定义可知,图的逻辑结构分为两部分:V和E的 集合,因此可以: 用一个一维数组存放图中所有顶点数据; 用一个二维数组存放顶点间关系(边或弧)的数据,称这个二维 数组为邻接矩陲。 邻接矩阵又分为有向图邻接矩陲和无向图邻接矩哇。 3 4 6 a.无向图G b.有向图G2 电子科技大学刘民岷 图 3
电子科技大学 刘民岷 图 3 2.1 邻接矩阵表示法 • 根据图的定义可知,图的逻辑结构分为两部分:V和E的 集合,因此可以: – 用一个一维数组存放图中所有顶点数据; – 用一个二维数组存放顶点间关系(边或弧)的数据,称这个二维 数组为邻接矩阵。 – 邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵。 1 2 3 4 5 a.无向图G 1 6 2 3 4 5 b.有向图G2
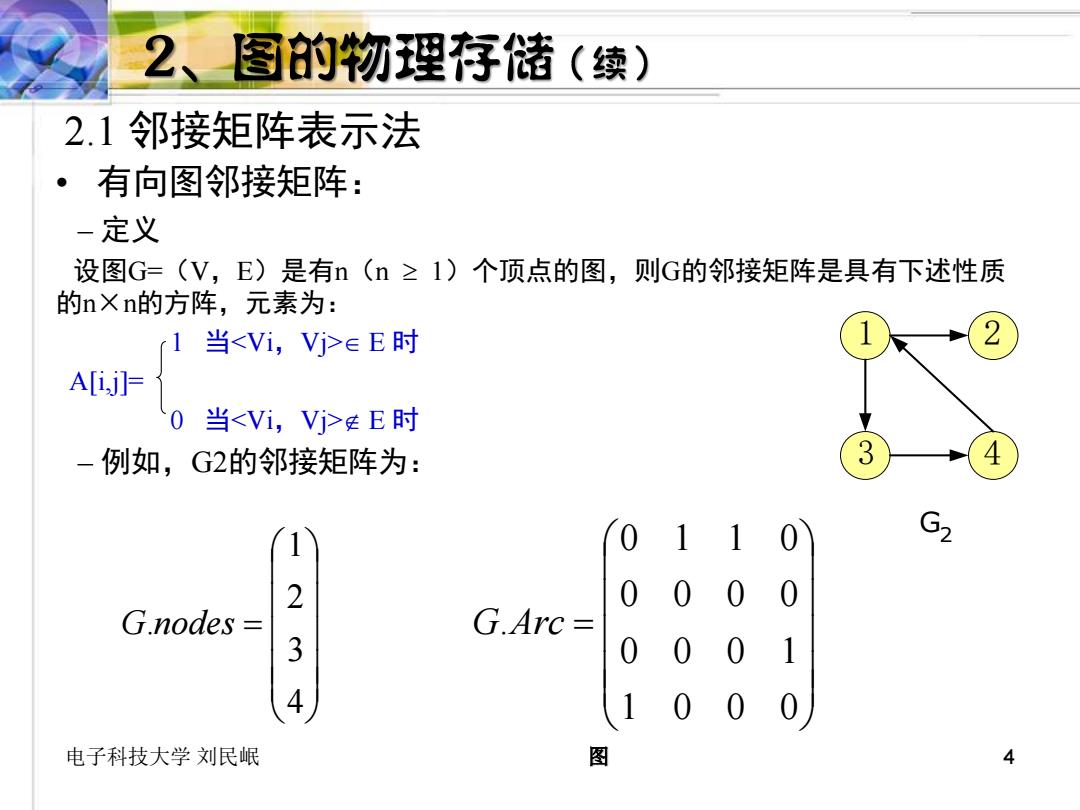
2、图的物理存储(续) 2.1邻接矩阵表示法 ·有向图邻接矩阵: -定义 设图G=(V,E)是有n(n≥I)个顶点的图,则G的邻接矩阵是具有下述性质 的nXn的方阵,元素为: 当∈E时 A[i.jl= 0 当E时 -例如,G2的邻接矩阵为: 3 G2 2 G.nodes G.Arc 3 4 电子科技大学刘民岷 图 4
电子科技大学 刘民岷 图 4 2.1 邻接矩阵表示法 • 有向图邻接矩阵: – 定义 设图G=(V,E)是有n(n 1)个顶点的图,则G的邻接矩阵是具有下述性质 的n×n的方阵,元素为: 1 当 E 时 A[i,j]= 0 当 E 时 – 例如,G2的邻接矩阵为: 1 2 3 4 G2 = 4 3 2 1 G.nodes = 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 G.Arc

2、图的物理存储(续) 2.1邻接矩阵表示法 ·无向图邻接矩阵: 定义 设图G=(V,E)是有n(n≥l)个顶点的无向图图,则G的邻接矩阵是 具有下述性质的n×n的方阵,元素为: 1当(Vi,Vj)eE时 A[ij]- 0 当(Vi,Vj)eE时 3 例如,G,的邻接矩阵为: 1 0 1 2 1 0 1 1 G.nodes= 3 G.Edge= 11 0 4 1 电子科技大学刘民岷 图 5
电子科技大学 刘民岷 图 5 2.1 邻接矩阵表示法 • 无向图邻接矩阵: – 定义 设图G=(V,E)是有n(n 1)个顶点的无向图图,则G的邻接矩阵是 具有下述性质的n×n的方阵,元素为: 1 当(Vi,Vj) E 时 A[i,j]= 0 当(Vi,Vj) E 时 – 例如,G1的邻接矩阵为: 1 2 3 4 G1 = 4 3 2 1 G.nodes = 0 1 0 0 1 1 0 0 1 0 1 1 0 1 1 0 G.Edge

2、图的物理存储(续) 2.1邻接矩阵表示法 求图中顶点的度: 借助邻接矩阵,可以很容易地求出图中顶点的度。 无向图邻接矩阵的第行(或第列) 的元素之和是顶点V的度。 例,G1中V2的度是3。 有向图邻接矩阵第行的元素之和为顶点V的出度;第列的元素 之和为顶点Vj的入度。例,G2中,V2的出度为0(第2行的元素之 和为0),V1的入度为1(第1列的元素之和为1)。 无向图G1 有向图 G2 0 1 1 0 3 0 11 10 00 0 G.Edge= G.Arc= 1 1 0 G 0 0 0 1 0 0 电子科技大学刘民岷 图 6
电子科技大学 刘民岷 图 6 2.1 邻接矩阵表示法 • 求图中顶点的度: 借助邻接矩阵,可以很容易地求出图中顶点的度。 – 无向图 邻接矩阵的第i行(或第i列)的元素之和是顶点Vi的度。 例,G1中V2的度是3。 – 有向图 邻接矩阵第i行的元素之和为顶点Vi的出度;第j列的元素 之和为顶点Vj的入度。例,G2中,V2的出度为0(第2行的元素之 和为0),V1的入度为1(第1列的元素之和为1)。 = 0 1 0 0 1 1 0 0 1 0 1 1 0 1 1 0 G.Edge = 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 G.Arc 无向图 G1 有向图 G2 1 2 3 4 G1 1 2 3 4 G2

2、图的物理存储(续) 2.2邻接表表示法 。 邻接表是图的一种链式存储结构。对图的每个顶点建立一个单链表 (n个顶点建立n个单链表),第个单链表中的结点包含顶点V的所有 邻接顶点。 在邻接表中,每个顶点由三个域组成: adjvex data nextarc 指向Vi的下一个 顶,点Vi的邻接点 邻接,点的指针 与边或孤有关的权值 ·每个单链表附设一个头结点,结构为: Vexdata firstarc 存放Vi信息 指向Vi单链表的第一个结点 电子科技大学刘民岷 图 7
电子科技大学 刘民岷 图 7 2.2 邻接表表示法 • 邻接表是图的一种链式存储结构。对图的每个顶点建立一个单链表 (n个顶点建立n个单链表),第i个单链表中的结点包含顶点Vi的所有 邻接顶点。 • 在邻接表中,每个顶点由三个域组成: • 每个单链表附设一个头结点,结构为: adjvex data nextarc 顶点Vi的邻接点 与边或弧有关的权值 指向Vi的下一个 邻接点的指针 Vexdata firstarc 存放Vi信息 指向Vi单链表的第一个结点

2、图的物理存储(续) 2.2邻接表表示法 。 邻接表的C语言描述 define MAXNODE typedef struct st arc fint adivex; adjvex data nextarc weighttype date; /孤的权值类型 struct st arc *nextarc; typedef struct nodetype vexdata; 顶点的数据类型 Vexdata firstarc struct st arc *firstarc; Headnode; Headnodes结构类型定义 Headnode adjlist[MAXNODE]; 电子科技大学刘民岷 图 8
电子科技大学 刘民岷 图 8 2.2 邻接表表示法 • 邻接表的C语言描述 adjvex data nextarc Vexdata firstarc # define MAXNODE typedef struct st_arc {int adivex; weighttype date; //弧的权值类型 struct st_arc *nextarc; } typedef struct {nodetype vexdata; //顶点的数据类型 struct st_arc *firstarc; }Headnode; //Headnode结构类型定义 Headnode adjlist[MAXNODE];
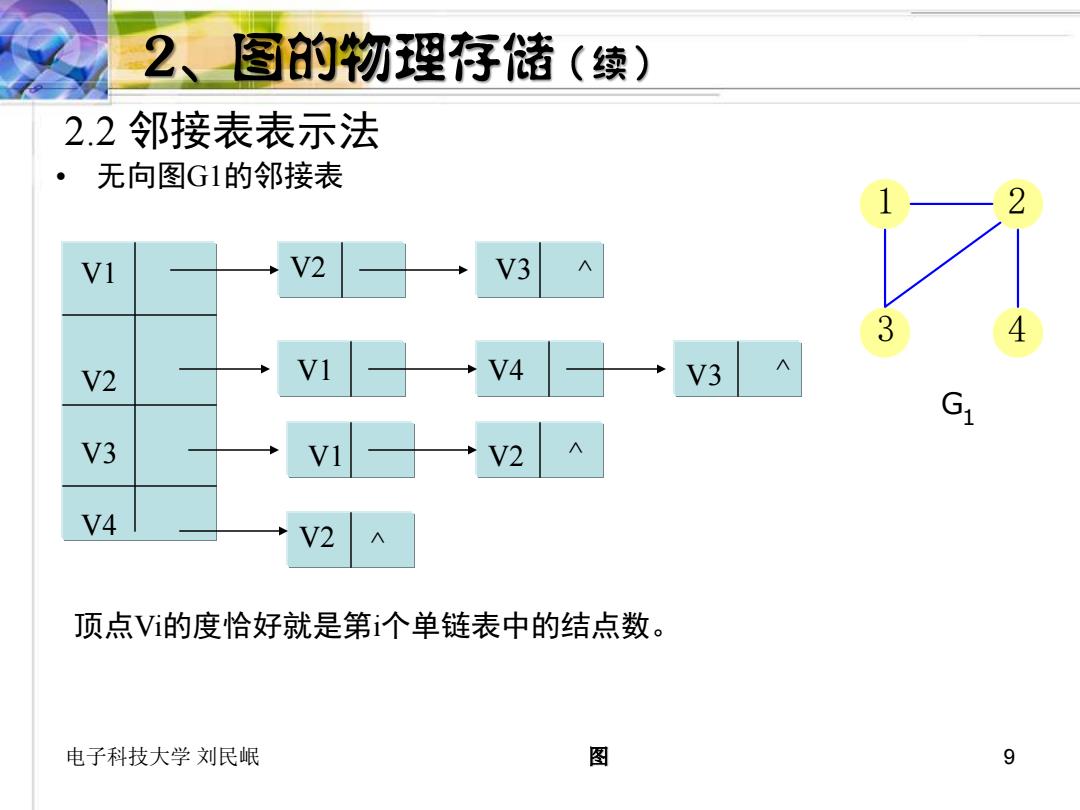
2、图的物理存储(续) 2.2邻接表表示法 ·无向图G1的邻接表 VI V2 V3 3 4 V2 V4 V3 S V3 V2 V4 V2 顶点V的度恰好就是第i个单链表中的结点数。 电子科技大学刘民岷 图 9
电子科技大学 刘民岷 图 9 2.2 邻接表表示法 • 无向图G1的邻接表 V1 V2 V3 V4 V2 V3 ^ V1 V4 V3 ^ V1 V2 ^ V2 ^ 顶点Vi的度恰好就是第i个单链表中的结点数。 1 2 3 4 G1
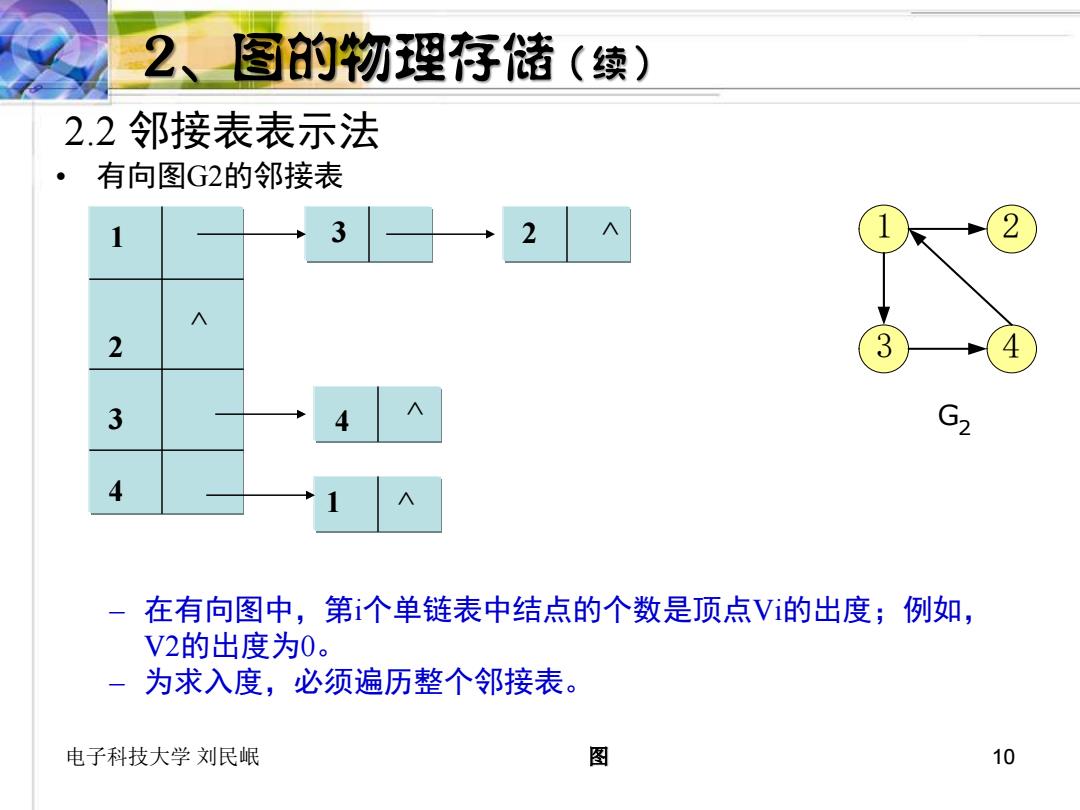
2、图的物理存储(续) 2.2邻接表表示法 ·有向图G2的邻接表 2 2 3 4 4 在有向图中,第个单链表中结点的个数是顶点V的出度;例如, V2的出度为0。 一为求入度,必须遍历整个邻接表。 电子科技大学刘民岷 图 10
电子科技大学 刘民岷 图 10 2.2 邻接表表示法 • 有向图G2的邻接表 – 在有向图中,第i个单链表中结点的个数是顶点Vi的出度;例如, V2的出度为0。 – 为求入度,必须遍历整个邻接表。 1 2 3 4 3 2 ^ 4 ^ 1 ^ ^ 1 2 3 4 G2