
电子斜技大学 软件技术基础 3.4数组 主讲教师:刘民岷 航空航天学院 a口2 软件技术基础课程组
软件技术基础 主讲教师:刘民岷 航空航天学院 软件技术基础课程组

1、数组的逻辑结构 数组是相同类型数据元素的有限集合; 数组中的各个分量称为数组元素; 。 每个数组元素值可以用数组名和一个下标值唯一的确定; 一 维数组是一种顺序表结构; 多维数组是一种特殊的线性结构,其中使用最多的是二维 数组。 电子科技大学刘民岷 数组 2
电子科技大学 刘民岷 数组 2 • 数组是相同类型数据元素的有限集合; • 数组中的各个分量称为数组元素; • 每个数组元素值可以用数组名和一个下标值唯一的确定; • 一维数组是一种顺序表结构; • 多维数组是一种特殊的线性结构,其中使用最多的是二维 数组
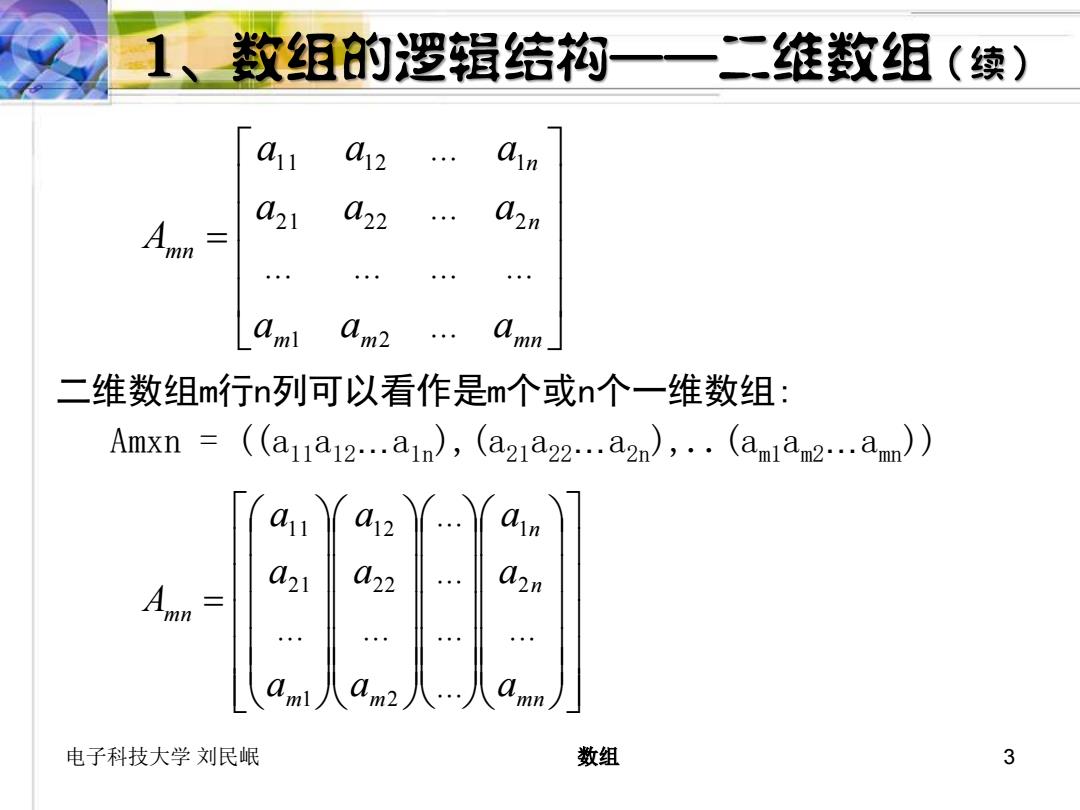
1、数组的逻辑结构一一二维数组(续) 1 012 . n 01 022 am 0m2 二维数组m行n列可以看作是m个或n个一维数组: Amxn = (a1a12.a1n),(a21a2.a2n),.(anla2…am) 02 021 02 Amn= 电子科技大学刘民岷 数组 3
电子科技大学 刘民岷 数组 3 二维数组m行n列可以看作是m个或n个一维数组: Amxn = ((a11a12…a1n),(a21a22…a2n),..(am1am2…amn)) = m n n n m m m n a a a a a a a a a A ... ... ... ... ... ... ... 2 1 2 2 2 1 2 1 2 1 1 1 = m m m n n n m n a a a a a a a a a A ... ... ... ... ... ... ... 1 2 2 1 2 2 2 1 1 1 2 1

2、数组的基本操作 数组有两种基本的操作: -给定下标,存取相应的数组元素; 一给定下标,修改相应数组元素的值。 ·上两种操作可以归结为: 一给定一组下标,确定与之相对应的数据元素存储地址。 数组是如何存储的呢 电子科技大学刘民岷 数组 4
电子科技大学 刘民岷 数组 4 数组有两种基本的操作: – 给定下标,存取相应的数组元素; – 给定下标,修改相应数组元素的值。 • 上两种操作可以归结为: – 给定一组下标,确定与之相对应的数据元素存储地址。 数组是如何存储的呢?
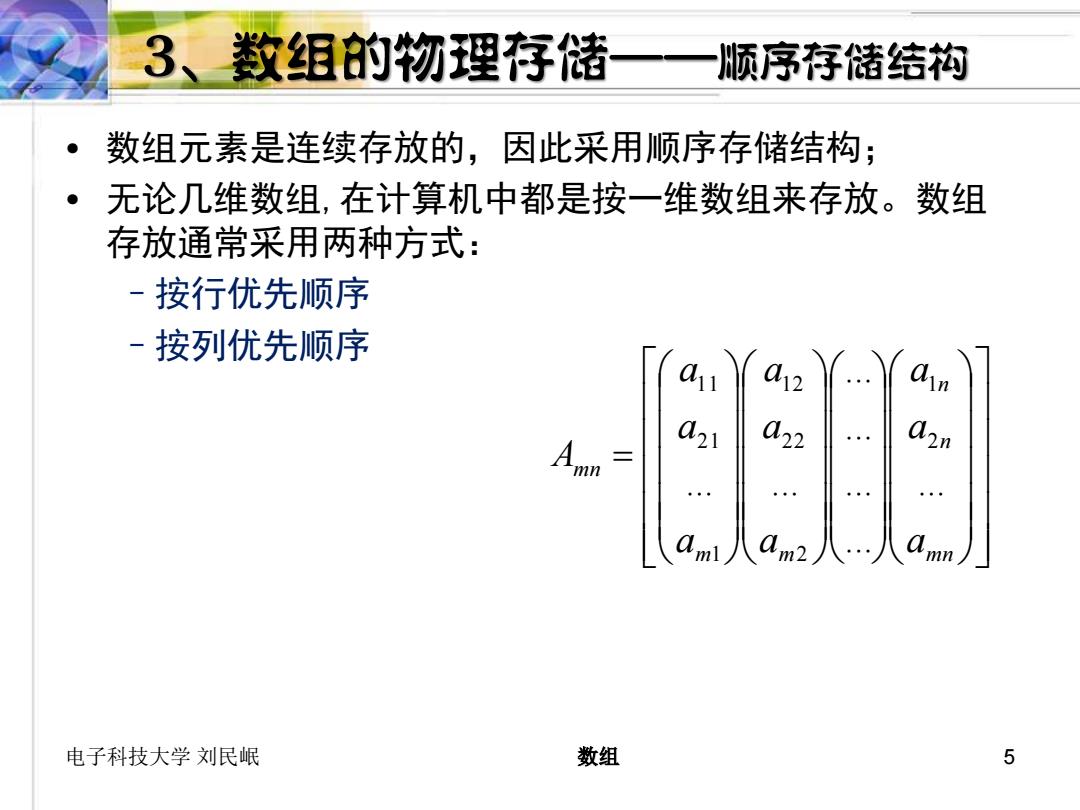
3、数组的物理存储 一一顺序存储结构 数组元素是连续存放的,因此采用顺序存储结构; 无论几维数组,在计算机中都是按一维数组来存放。数组 存放通常采用两种方式: -按行优先顺序 一按列优先顺序 02 021 022 02n a2 人an 电子科技大学刘民岷 数组 5
电子科技大学 刘民岷 数组 5 • 数组元素是连续存放的,因此采用顺序存储结构; • 无论几维数组,在计算机中都是按一维数组来存放。数组 存放通常采用两种方式: –按行优先顺序 –按列优先顺序 = m n n n m m m n a a a a a a a a a A ... ... ... ... ... ... ... 2 1 2 2 2 1 2 1 2 1 1 1

3.1二维数组按行优先存储 按行优先顺序存储是将数组看作若干个行向量。例如,二维 数组An,可以看作m个行向量,每个行向量n个元素。数组中 的每个元素由元素的两个下标表达式唯一的确定。 地址计算公式: LOC(ai)=LOC(a)+((i-1)Xn+(j-1))XS 其中,S是每个元素所占的存储单元。 二维数组按行优先存储举例 电子科技大学刘民岷 数组 6
电子科技大学 刘民岷 数组 6 按行优先顺序存储是将数组看作若干个行向量。例如,二维 数组Amn,可以看作m个行向量,每个行向量n个元素。数组中 的每个元素由元素的两个下标表达式唯一的确定。 地址计算公式: LOC(aij)=LOC(a11)+((i-1)×n+(j-1))×S 其中,S是每个元素所占的存储单元。 二维数组按行优先存储举例

3.1二维数组按行优先存储(续) 有二维数组Am如下: a12 a13 14 A34= a21 422 23 024 31 032 C33 034 其存储方式及各元素存储位置计算如下: LOC(aj)=LOC(a)+((i-1)Xn+(j-1))XS 12345678 910 1112 (a11,a12,a13,a14),(a21,a22,a23,a24),(a31,a32,a33,a34) L0C(a23)=L0C(a1i+(2-1)×4+(3-1)×1=7 L0C(a34)=1+(3-1)×4+(4-1)×1=12 L0C(a14F1+(1-1)×4+(4-1)×1=4 电子科技大学刘民岷 数组 7
电子科技大学 刘民岷 数组 7 有二维数组Amn如下: • 其存储方式及各元素存储位置计算如下: • LOC(aij)=LOC(a11)+((i-1)×n+(j-1))×S 1 2 3 4 5 6 7 8 9 10 11 12 ((a11,a12,a13,a14),(a21,a22,a23,a24),(a31,a32,a33,a34)) LOC(a23)= LOC(a11)+((2-1) × 4+(3-1))×1= 7 LOC(a34)= 1 +((3-1) × 4 +(4-1)) ×1= 12 LOC(a14)= 1 +((1-1)×4 +(4-1)) ×1= 4 = 3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 4 3 4 a a a a a a a a a a a a A

3.2二维数组按列优先存储 按列优先顺序存放是将数组看作若干个列向量。例如,二 维数组Am,可以看作n个列向量,每个列向量m个元素。 数组中的每个元素由元素的两个下标表达式唯一的确定。 地址计算公式: LOC(aj)=LOC (an)+((j-1)Xm+(i-1))XS 其中,S是每个元素所占的存储单元。 二维数组按列优先存储举例 电子科技大学刘民岷 数组 8
电子科技大学 刘民岷 数组 8 按列优先顺序存放是将数组看作若干个列向量。例如,二 维数组Amn,可以看作n个列向量,每个列向量m个元素。 数组中的每个元素由元素的两个下标表达式唯一的确定。 地址计算公式: LOC(aij)=LOC(a11)+((j-1)×m+(i-1))×S 其中,S 是每个元素所占的存储单元。 二维数组按列优先存储举例

3.2二维数组按列优先存储(续) ,有二维数组如下: 012 13 14 A34= a21a22 023 024 a31 32 033 034 ·其存储方式及各元素存储位置计算如下: L0C(a=L0C(au)+(G-1)Xm+i-1))XS 123456789 101112 (a1,a21,a3i),(a12,a22,a2,(a13,a23,a3,(a14,a24,a34) L0C(a23)=L0C(au)+3-1)x3+(2-1)=8 L0C(a4)=1+(4-1)x3+3-1)=12 L0C(a4)=1+(4-1)x3+(1-1)=10 电子科技大学刘民岷 数组 9
电子科技大学 刘民岷 数组 9 • 有二维数组如下: • 其存储方式及各元素存储位置计算如下: LOC(aij)=LOC(a11)+((j-1)×m+(i-1))×S 1 2 3 4 5 6 7 8 9 10 11 12 (a11,a21,a31),(a12,a22,a32),(a13,a23,a33),(a14,a24,a34)) LOC(a23)= LOC(a11)+(3-1)x 3 +(2-1)= 8 LOC(a34)= 1 + (4-1)x 3 + (3-1) = 12 LOC(a14)= 1 + (4-1)x 3 + (1-1) = 10 = 3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 4 3 4 a a a a a a a a a a a a A

特殊数组的压缩存储 引入: 实际工程问题中推导出的数组常常是高阶、含大量零元素的矩阵,或 者是些有规律排列的元素。为了节省存储空间,通常是对这类矩阵进 行压缩存储。 压缩的含义是: 一相同值的多个元素占用一个存储单元; 一零元素不分配存储单元。 电子科技大学刘民岷 数组 10
电子科技大学 刘民岷 数组 10 引入: 实际工程问题中推导出的数组常常是高阶、含大量零元素的矩阵,或 者是些有规律排列的元素。为了节省存储空间,通常是对这类矩阵进 行压缩存储。 压缩的含义是: – 相同值的多个元素占用一个存储单元; – 零元素不分配存储单元