
第二章流体静力学 Fluid Statics 2025-6-18 1
2025-6-18 1

Chapter 2 Fluid Statics 流体静力学 Hydraulics 研究流体的平衡和机械运动规律 Fluid Statics 研究液体平衡规律 粘滞力是否 起作用? ·静止状态 ·相对平衡状态
Chapter 2 Fluid Statics Hydraulics Fluid Statics 研究流体的平衡和机械运动规律 研究液体平衡规律 • 静止状态 • 相对平衡状态 粘滞力是否 起作用 ?

Chapter 2 Fluid Statics 2-1静水压强及其特性 1.静水压力与静水压强 静水压力: 静止液体作用在与之接触的 表面上的水压力P 静水压强: 当么A→0时, △P lim △A-→0 △A
Chapter 2 Fluid Statics 1. 静水压力与静水压强 静水压力: 静止液体作用在与之接触的 表面上的水压力 P 静水压强: 当 A 0 时, A P p A 0 lim

Chapter 2 Fluid Statics 静水压强 均布(底板): △P p △A 非均布(闸门): △P p=lim 4A-→0 ∠A N/m2=Pa)
Chapter 2 Fluid Statics 均布(底板): P p A 非均布(闸门): A P p A 0 lim ( N / m2 = Pa )

Chapter 2 Fluid Statics 静水压强的特性 特性一: 压强垂直作用面,且沿内法线方向. (静水压强的方向与受压面垂直,并指向 受压面)
Chapter 2 Fluid Statics 压强垂直作用面,且沿内法线方向. ( 静水压强的方向与受压面垂直,并指向 受压面) 特性一:
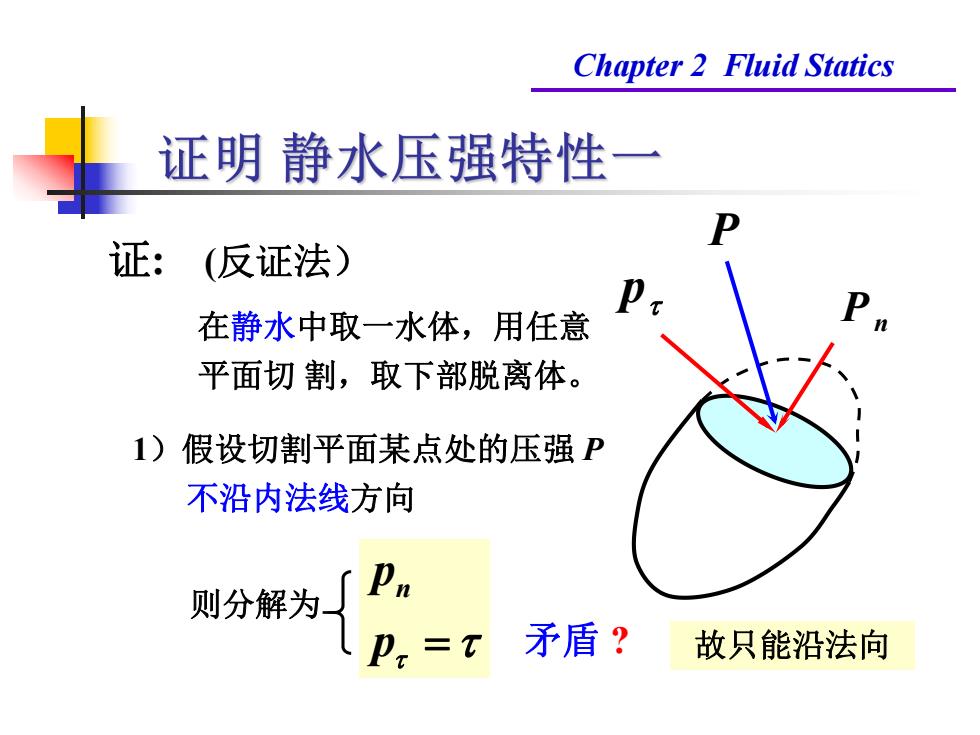
Chapter 2 Fluid Statics 证明静水压强特性 证: (反证法) 在静水中取一水体,用任意 平面切割,取下部脱离体。 1)假设切割平面某点处的压强P 不沿内法线方向 则分解为 卫,=x矛盾? 故只能沿法向
Chapter 2 Fluid Statics 证: (反证法) 在静水中取一水体,用任意 平面切 割,取下部脱离体。 1)假设切割平面某点处的压强 P 不沿内法线方向 则分解为 p pn Pn p 矛盾 ? P 故只能沿法向
Chapter 2 Fluid Statics 证明静水压强特性一(续) 2)假设沿外法向 矛盾? 液体不能受拉 所以静水压强的方向就是唯一的 沿作用面的 内法线方向
Chapter 2 Fluid Statics 所以静水压强的 方向就是唯一的 2)假设沿外法向 矛盾 ? 液体不能受拉 沿作用面的 内法线方向

Chapter 2 Fluid Statics 静水压强特性二 特性二: 任一点静水压强的大小与受压面方向无关, (或作用与同一点上各方向静水压强大小相 等与作用面方向无关)
Chapter 2 Fluid Statics 任一点静水压强的大小与受压面方向无关. (或 作用与同一点上各方向静水 压强大小相 等与作用面方向无关) 特性二:
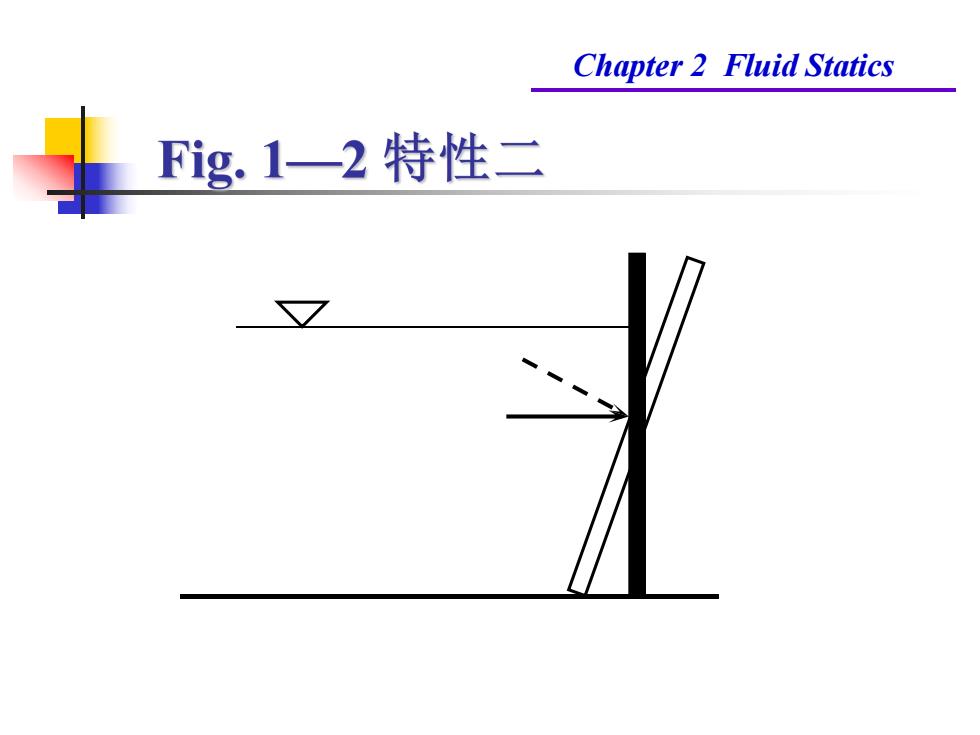
Chapter 2 Fluid Statics Fig.1一2特性二
Chapter 2 Fluid Statics
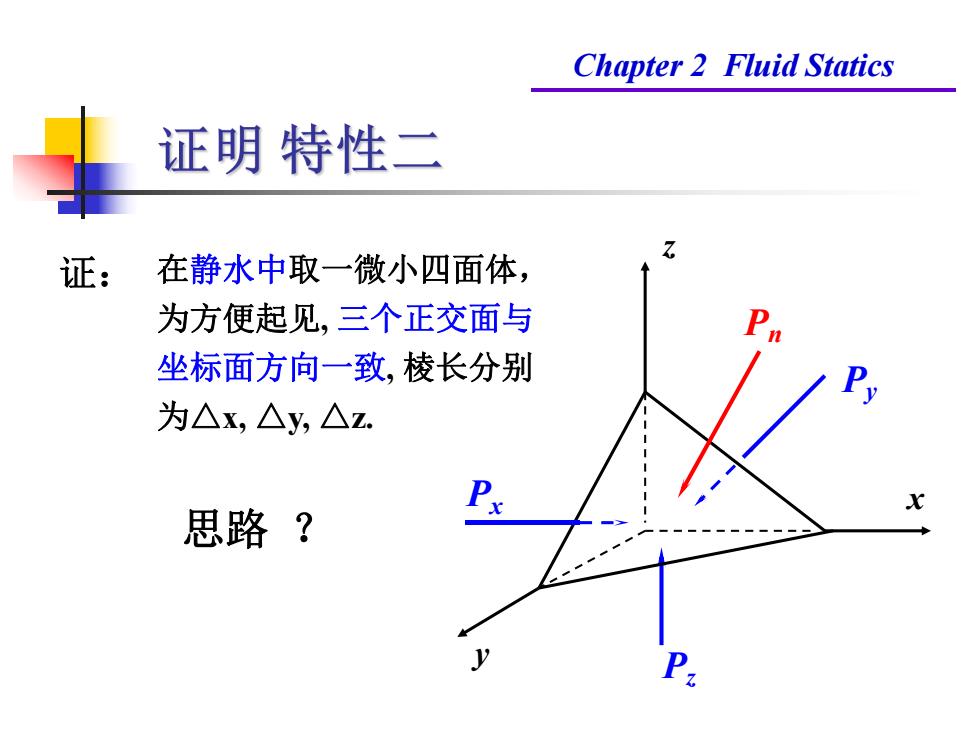
Chapter 2 Fluid Statics 证明特性二 证: 在静水中取一微小四面体, 为方便起见,三个正交面与 坐标面方向一致,棱长分别 为△x,△y,△z. 思路?
Chapter 2 Fluid Statics x y z 在静水中取一微小四面体, 为方便起见, 三个正交面与 坐标面方向一致, 棱长分别 为△x, △y, △z. 证: Pn Py Px Pz 思路 ?