
Recursion Examples
Recursion Examples

Recursion (review)
Recursion (review)
Recursion (review) Scenario:You are waiting in line for a concert.You can't see the front of the line,but you want to know your place in the line. The person at the front,knows they are at the front! Base case You ask the person in front of you:"what is your Recursive call place in the line?” When the person in front of you figures it out and Use the solution to tells you,add one to that answer. the smaller problem
Recursion (review) Scenario: You are waiting in line for a concert. You can't see the front of the line, but you want to know your place in the line. Base case Recursive call Use the solution to the smaller problem You ask the person in front of you: “what is your place in the line?” When the person in front of you figures it out and tells you, add one to that answer. The person at the front, knows they are at the front!

Iteration vs.Recursion Iteration and recursion are somewhat related ● Converting iteration to recursion is formulaic,but converting recursion to iteration can be more tricky Iterative Recursive def fact_iter(n): deffact(n): total,k=1,1 ifn==0: whilek <n: return 1 total,k total*k,k+1 else: return total return n*fact(n-1)】 m n!=Ik nn(n-1)!otiherwise if n 0 k=1 Names:n,total,k,fact_iter Names:n,fact
Iteration vs. Recursion ● Iteration and recursion are somewhat related ● Converting iteration to recursion is formulaic, but converting recursion to iteration can be more tricky def fact_iter(n): total, k = 1, 1 while k <= n: total, k = total*k, k+1 return total def fact(n): if n == 0: return 1 else: return n * fact(n-1) Iterative Recursive Names: n, total, k, fact_iter Names: n, fact

Sum Digits Let's implement a recursive function to sum all the digits of 'n'. Assume 'n'is positive. def sum_digits(n): """Calculates the sum of the digits 'n'. 1.One or more base >>sum_digits(8) cases 8 sum_digits(18) 2.One or more >>> 9 recursive calls >>> sum_digits(2018) with simpler 11 arguments. I 1 II ”大*火 YOUR CODE HERE 3.Using the +*★” recursive call to solve our larger problem
Sum Digits Let’s implement a recursive function to sum all the digits of `n`. Assume `n` is positive. def sum_digits(n): """Calculates the sum of the digits `n`. >>> sum_digits(8) 8 >>> sum_digits(18) 9 >>> sum_digits(2018) 11 """ "*** YOUR CODE HERE ***" 1. One or more base cases 2. One or more recursive calls with simpler arguments. 3. Using the recursive call to solve our larger problem

Sum Digits 1 def sum_digits(n): 2 """Calculates the sum of the digits n 3 >>sum_digits(8) 4 8 5 >>sum_digits(18) 6 9 7 >>sum_digits(2018) 8 11 9 111111 10 if n 10: 11 return n 12 else: 13 all_but_last,last n /10,n 10 14 return sum_digits(all_but_last)+last
Sum Digits 1 def sum_digits(n): 2 """Calculates the sum of the digits n 3 >>> sum_digits(8) 4 8 5 >>> sum_digits(18) 6 9 7 >>> sum_digits(2018) 8 11 9 """ 10 if n < 10: 11 return n 12 else: 13 all_but_last, last = n // 10, n % 10 14 return sum_digits(all_but_last) + last

Order of Recursive Calls
Order of Recursive Calls

Demo Cascade Goal:Print out a cascading tree of a positive integer n. >>> cascade(486) ldeas: :486 If n is a single digit,just print it out! ==== 48 Otherwise,let cascade(n /10) 4 take care of the middle ===================== 48 and print(n)around it! 486 >>> cascade(48) 1 def cascade(n): 48 2 if n>cascade(4) 6 icascade(n 77 10)) ==号=== 4 7 iprint(n)_
1 def cascade cascade(n): 2 if n >> cascade(486) 486 48 4 48 486 >>> cascade(48) 48 4 48 >>> cascade(4) 4 Ideas: ● If n is a single digit, just print it out! ● Otherwise, let cascade(n // 10) take care of the middle and print(n) around it Demo
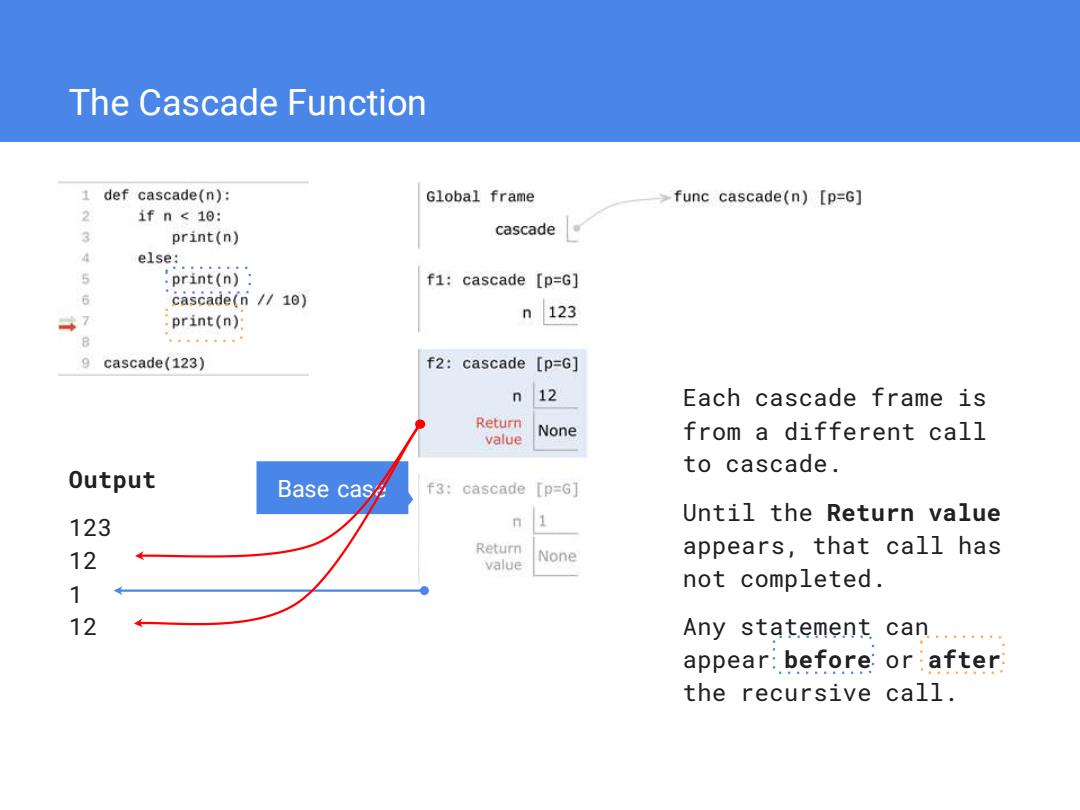
The Cascade Function 1 def cascade(n): Global frame func cascade(n)[p=G] 1fn<10: 2 print(n) cascade 4 else: 5 :print(n): f1:cascade [p=G] 6 cascade(n//10) 47 print(n) n123 8 。中。。t。。。 9 cascade(123) f2:cascade [p=G] 12 Each cascade frame is Return value None from a different call to cascade. Output Base cas∥ f3:cascade【p=G] 123 n 1 Until the Return value Return 12 value None appears,that call has 1 not completed. 12 Any statement can...... appear:before:or after the recursive call
The Cascade Function Each cascade frame is from a different call to cascade. Until the Return value appears, that call has not completed. Any statement can appear before or after the recursive call. Output 123 12 1 12 Base case

Demo Two Implementations of Cascade 1 def cascade(n): 1 def cascade(n): 2 if n 10: 2 print(n) 3 print(n) 3 ifn>=-10: 4 else: 4 cascade(n /10) 5 print(n) 5 print(n) 6 cascade(n /10) 7 print(n) If two implementations are equally clear,then shorter is usually better ● In this case,the longer implementation might be more clear When learning to write recursive functions,put the base case/s first
Two Implementations of Cascade ● If two implementations are equally clear, then shorter is usually better ● In this case, the longer implementation might be more clear ● When learning to write recursive functions, put the base case/s first 1 def cascade(n): 2 if n = 10: 4 cascade(n // 10) 5 print(n) Demo