
信息检索与数据挖掘-论文阅读 Neural Ordinary Differential Equations 吴宁谦SA18006140
信息检索与数据挖掘-论文阅读 Neural Ordinary Differential Equations 吴宁谦 SA18006140

Neural Ordinary Differential Equations 摘要 选有NIPS Ricky T.Q.Chen",Yulia Rubanova*,Jesse Bettencourt*,David Duvenaud 2018 best paper University of Toronto,Vector Institute Toronto,Canada {rtqichen,rubanova,jessebett,duvenaud)Ocs.toronto.edu 论文介绍了一个新的深度神经网络家族NeuralODE。 它对神经网络的隐状态的导数进行参数化,使用微 分方程求解器计算网络的输出。这类模型只需要常 数级的内存成本,并且能在计算速度和模型精度之 间进行权衡。 论文在连续深度残差网络与连续时间隐变量模型上,进 行了验证实验。 论文提出了连续标准化流(CNF),它是一种通过最大似然 进行训练的生成模型。 论文展示了如何通过ODE求解器进行可扩展的反向传播, 允许大规模模型中的端到端训练
摘要 论文介绍了一个新的深度神经网络家族NeuralODE。 它对神经网络的隐状态的导数进行参数化,使用微 分方程求解器计算网络的输出。这类模型只需要常 数级的内存成本,并且能在计算速度和模型精度之 间进行权衡。 论文在连续深度残差网络与连续时间隐变量模型上,进 行了验证实验。 论文提出了连续标准化流(CNF),它是一种通过最大似然 进行训练的生成模型。 论文展示了如何通过ODE求解器进行可扩展的反向传播, 允许大规模模型中的端到端训练。 选自NIPS 2018 best paper

介绍-基本思想 诸如残差网络,递归神经网络(RNN),或标准化 流等神经网络构架中一般会含有重复的层块来 有序地保留信息。一般可以写成: ht+1 ht f(ht,0t) where t∈{0..T}and ht∈RD 这可以看成是一个微分方程的欧拉迭代求解。 当层数趋于无穷,△t趋于零时,上式可以化为: dh(t)=f(h(t),t.0) dt
介绍 – 基本思想 诸如残差网络,递归神经网络(RNN),或标准化 流等神经网络构架中一般会含有重复的层块来 有序地保留信息。一般可以写成: 这可以看成是一个微分方程的欧拉迭代求解。 当层数趋于无穷,Δt趋于零时,上式可以化为:
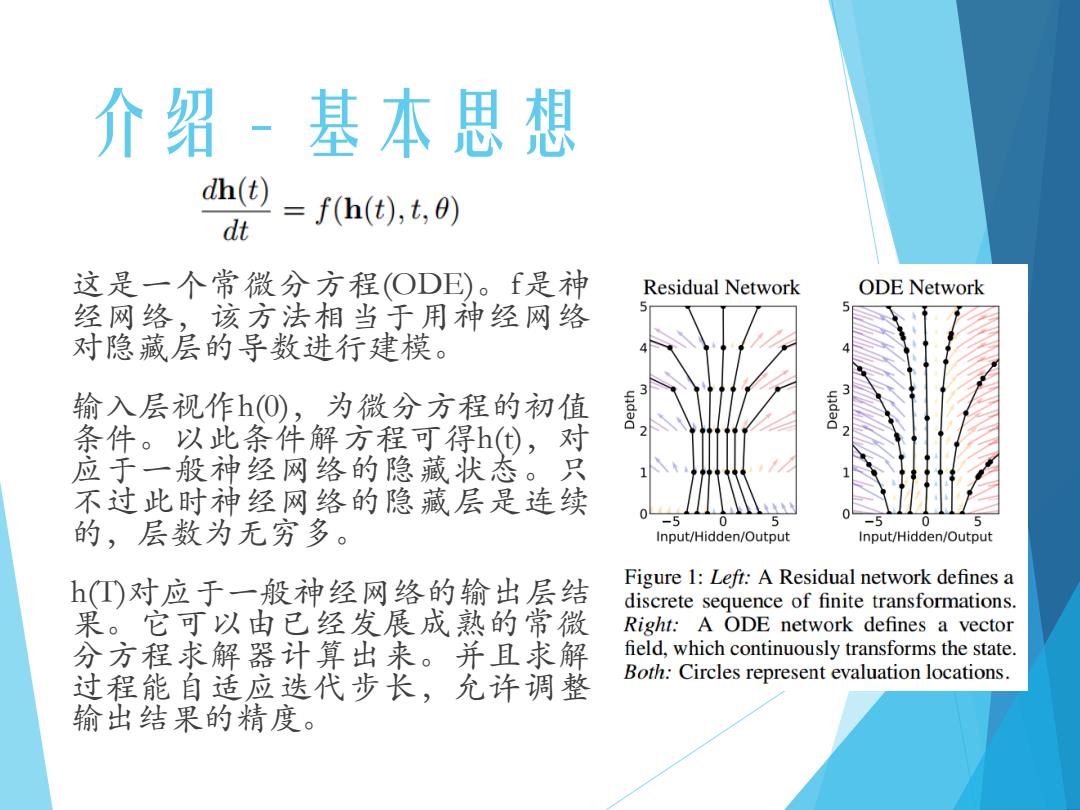
介绍-基本思想 dh(t) f(h(t),t,0) dt 这是一个常微分方程(ODE)。f是神 Residual Network ODE Network 经网络,该方法相当于用神经网络 对隐藏层的导数进行建模。 输入层视作h(O),为微分方程的初值 条件。以此条件解方程可得h(①,对 应于一般神经网络的隐藏状态。 不过此时神经网络的隐藏层是连续 -5 的,层数为无穷多。 Input/Hidden/Output Input/Hidden/Output h(T)对应于一般神经网络的输出层结 Figure 1:Left:A Residual network defines a discrete sequence of finite transformations. 果。它可以由已经发展成熟的常微 Right:A ODE network defines a vector 分方程求解器计算出来。并且求解 field,which continuously transforms the state 过程能自适应迭代步长,允许调整 Both:Circles represent evaluation locations. 输出结果的精度
介绍 – 基本思想 这是一个常微分方程(ODE)。f是神 经网络,该方法相当于用神经网络 对隐藏层的导数进行建模。 输入层视作h(0),为微分方程的初值 条件。以此条件解方程可得h(t),对 应于一般神经网络的隐藏状态。只 不过此时神经网络的隐藏层是连续 的,层数为无穷多。 h(T)对应于一般神经网络的输出层结 果。它可以由已经发展成熟的常微 分方程求解器计算出来。并且求解 过程能自适应迭代步长,允许调整 输出结果的精度

介绍-ODE的优点 内存效率高。不需要存储任何中间变量,内存空间 复杂度为○(1)。 允许自适应计算。现代ODE求解器已经发展了120 余年,现在的求解器可以在运行中调整其评估策略 以达到所要求的精度水平。 参数效率高。在相同的性能下比传统的神经网络所 需参数更少。 可扩展和可逆。结合标准化流与ODE,可以让计 算更容易,突破了标准化流的性能瓶颈。 更灵活。ODE连续时间序列模型,允许接入任意 时间点的训练数据,无需固定的采样间隔,能解决 更复杂的问题
介绍 – ODE的优点 内存效率高。不需要存储任何中间变量,内存空间 复杂度为O(1)。 允许自适应计算。现代ODE求解器已经发展了120 余年,现在的求解器可以在运行中调整其评估策略 以达到所要求的精度水平。 参数效率高。在相同的性能下比传统的神经网络所 需参数更少。 可扩展和可逆。结合标准化流与ODE,可以让计 算更容易,突破了标准化流的性能瓶颈。 更灵活。ODE连续时间序列模型,允许接入任意 时间点的训练数据,无需固定的采样间隔,能解决 更复杂的问题

ODE解的反向传播 训练连续深度的网络的主要技术难,点是计 算ODE解的反向转播。 直接按照前向传播的计算路径反向传播是 一个很直观的想法,但是会带来较高的存 储成本并引入额外的数值误差。 论文采取了使用伴随方法(adjoint method)[Pontryagin et al.,1962)】计算梯度的 策略。该方法通过时间上反向求解另一个 增广ODE来逼近计算梯度。之后的梯度即 可进一步用于参数的更新该方法的代价与 问题规模成线性关系,内存消耗较低,并 能够控制数值误差
ODE解的反向传播 训练连续深度的网络的主要技术难点是计 算ODE解的反向转播。 直接按照前向传播的计算路径反向传播是 一个很直观的想法,但是会带来较高的存 储成本并引入额外的数值误差。 论 文 采 取 了 使 用 伴 随 方 法 (adjoint method)[(Pontryagin et al., 1962)]计算梯度的 策略。该方法通过时间上反向求解另一个 增广ODE来逼近计算梯度。之后的梯度即 可进一步用于参数的更新该方法的代价与 问题规模成线性关系,内存消耗较低,并 能够控制数值误差

伴随方法 z即之前的h 若损失函数L定义如下:(z1为神经网络的输出) Let》=L(心f,toan)=L(ODESole(.)foi.on aLaL aLaL 反向传播的目标是求出 Oz(to),80,Oto'Ot 伴随项定义为a(t)=-L/z(t)相当于隐层的梯度。 则由链式法则可以旅出 =-a(t)Of(z(t).t.0) OZ 这其实也是一个ODE,初值为L/z(t),通过反向求解这 个ODE即可求得 aL 8z(to) 解另一个oDE胎-[广agrr0无 08 aL 可求得
伴随方法 若损失函数L定义如下:(zt_1为神经网络的输出) 反向传播的目标是求出 伴随项定义为 相当于隐层的梯度。 则由链式法则可以推出 这其实也是一个ODE,初值为 ,通过反向求解这 个ODE即可求得 解另一个ODE 可求得 z即之前的h

伴随方法 实现时可将ODE拼起来一次性求解,算法如下: Input:dynamics parameters 0,start time to,stop time t,final state z(t),loss gradient L/z() 器=%'f26,9 Compute gradient w.r.t.t s0=z(1,20,0,-8别 Define initial augmented state def aug_dynamics([z(t),a(t),-,-],t,0): Define dynamics on augmented state return[f(z(t)t,60),-a(t)r影,-a(t)r%,-a(t)r影] Concatenate time-derivatives o),ODESolve(so,aug dynamics,0) aL Solve reverse-time ODE return aLaLaLaL az(to)’a0,8to’8t Return all gradients 算法中,ODESolve的格式如下: 以正向传播的ODE为例,ODESolve(z(),ft0,t1)表示从t0时刻 开始令z()以变化率f进行演化,即f在t上的积分,最后通过积 分求得并输出z()。ODE的求解已经的发展成熟,该部分可 以看作 正个黑盒,无需记录其中的任何中间步骤。 求出了而之后,通过梯度下降法即可更新网络中的参数
伴随方法 实现时可将ODE拼起来一次性求解,算法如下: 算法中,ODESolve的格式如下: 以正向传播的ODE为例,ODESolve(z(t0 ),f,t0,t1)表示从t0时刻 开始令z(t0 )以变化率f进行演化,即f在t上的积分,最后通过积 分求得并输出z(t1 )。ODE的求解已经的发展成熟,该部分可 以看作一个黑盒,无需记录其中的任何中间步骤。 求出了 之后,通过梯度下降法即可更新网络中的参数
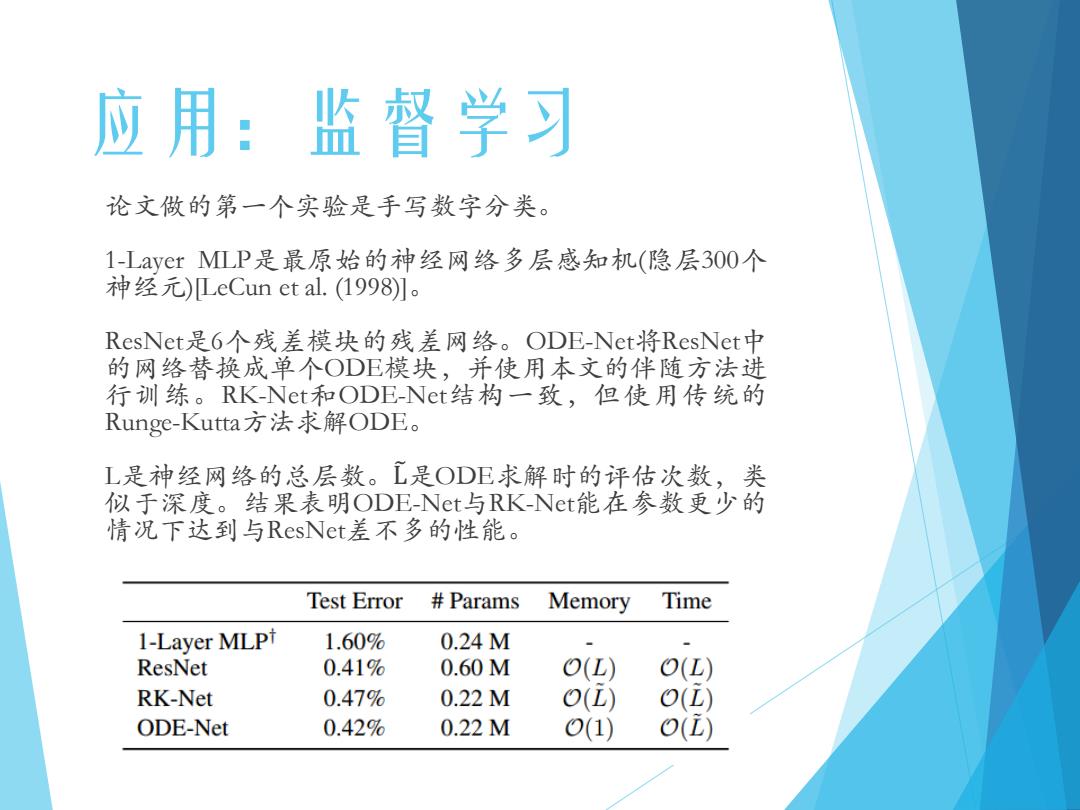
应用:监督学习 论文做的第一个实验是手写数字分类。 1-Layer MLP是最原始的神经网络多层感知机(隐层300个 神经元)LeCun et al..(1998)]。 ResNet是6个残差模块的残差网络。ODE-Net将ResNet中 的网络替换成单个ODE模块,并使用本文的伴随方法进 行训练。RK-Net和ODE-Net结构一致,但使用传统的 Runge-Kutta方法求解ODE。 L是神经网络的总层数。工是ODE求解时的评估次数,类 似于深度。结果表明ODE-Net与RK-Net能在参数更少的 情况下达到与ResNet差不多的性能。 Test Error Params Memory Time 1-Layer MLPt 1.60% 0.24M ResNet 0.41% 0.60M O(L) O(L) RK-Net 0.47% 0.22M O(L) O() ODE-Net 0.42% 0.22M 0(1) o()
应用:监督学习 论文做的第一个实验是手写数字分类。 1-Layer MLP是最原始的神经网络多层感知机(隐层300个 神经元)[LeCun et al. (1998)]。 ResNet是6个残差模块的残差网络。ODE-Net将ResNet中 的网络替换成单个ODE模块,并使用本文的伴随方法进 行训练。RK-Net和ODE-Net结构一致,但使用传统的 Runge-Kutta方法求解ODE。 L是神经网络的总层数。L෨是ODE求解时的评估次数,类 似于深度。结果表明ODE-Net与RK-Net能在参数更少的 情况下达到与ResNet差不多的性能
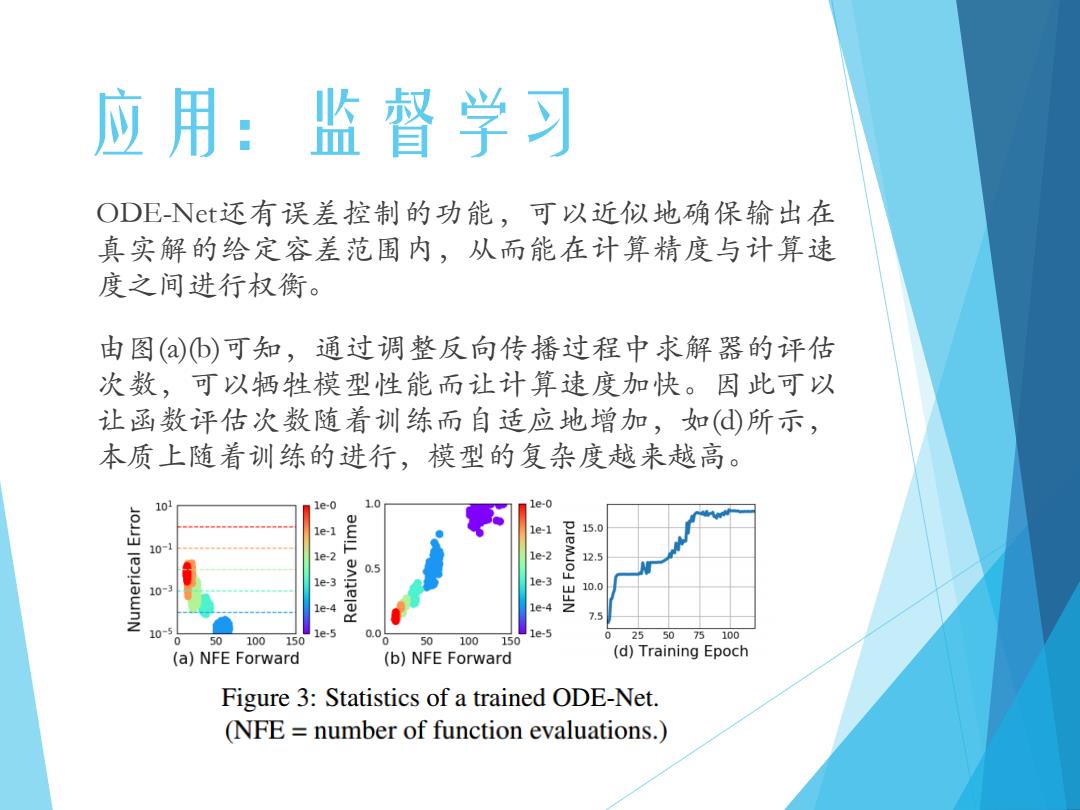
应用:监督学习 ODE-Nt还有误差控制的功能,可以近似地确保输出在 真实解的给定容差范围内,从而能在计算精度与计算速 度之间进行权衡。 由图(b)可知,通过调整反向传播过程中求解器的评估 次数,可以牺牲模型性能而让计算速度加快。因此可以 让函数评估次数随着训练而自适应地增加,如(d所示, 本质上随着训练的进行,模型的复杂度越来越高。 10 1e-0 10 1e-0 1e-1 le-1 15.0 10-1 1e-2 1e-2 12.5 0.5 1e-3 1e3 10 10.0 1e-4 3JN 7.5 10- 1e-5 0.0 1e-5 0 0 50 100 150 50100150 255075100 (a)NFE Forward (b)NFE Forward (d)Training Epoch Figure 3:Statistics of a trained ODE-Net. (NFE number of function evaluations.)
应用:监督学习 ODE-Net还有误差控制的功能,可以近似地确保输出在 真实解的给定容差范围内,从而能在计算精度与计算速 度之间进行权衡。 由图(a)(b)可知,通过调整反向传播过程中求解器的评估 次数,可以牺牲模型性能而让计算速度加快。因此可以 让函数评估次数随着训练而自适应地增加,如(d)所示, 本质上随着训练的进行,模型的复杂度越来越高