
BIT FUNNEL:REVISITING SIGNATURES FOR SEARCH 信息检索与数据挖掘研讨报告 凌华泽 20190521 Goodwin B,Hopcroft M,Luu D,et al.BitFunnel:Revisiting signatures for search[C]//Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval.ACM,2017:605-614
-----信息检索与数据挖掘研讨报告 凌华泽 20190521 Goodwin B, Hopcroft M, Luu D, et al. BitFunnel: Revisiting signatures for search[C]//Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 2017: 605-614

INTRODUCTION -BitFunnel Signature-based approach Bloom filter Four Challenges ·查询词项时需要查看每个文件的signature higher rank rows ·存在一定的误报率 frequency-conscious signature ·文件大小存在差异,signatur需要适应最大文件 shard the corpus ·基于签名的方案不是众所周知的问题 a cost model
BitFunnel Signature-based approach Bloom filter Four Challenges 查询词项时需要查看每个文件的signature higher rank rows 存在一定的误报率 frequency-conscious signature 文件大小存在差异,signatur需要适应最大文件 shard the corpus 基于签名的方案不是众所周知的问题 a cost model

Q A B C D E M N O P 0 0 BACK GROUND 2 1 00 00100 00 3 3 4 5 .Bit-Sliced Signature 1 6 0 6 10 0 ·这种方法将签名向量从行转换成列以方便 8 0 8888 同时查询多个文档 9 1 9 10 0 10 ·每个文档对应保存16位签名的列,每行对 0 11 对应于文档签名中的位 0 12 13 0 13 ·文档集C={A..) 14 00 150 15100 000 ·查询项Q A B O P .Bit-Sliced Blocked Signature 2 5 ·多个文件公用一列,以减小行的长度 9 01 2n5n9 0100010000000000 A B C D E FG H IJ K L M N O P
Bit-Sliced Signature 这种方法将签名向量从行转换成列以方便 同时查询多个文档 每个文档对应保存16位签名的列,每行对 对应于文档签名中的位 文档集C={A….P} 查询项Q Bit-Sliced Blocked Signature 多个文件公用一列,以减小行的长度
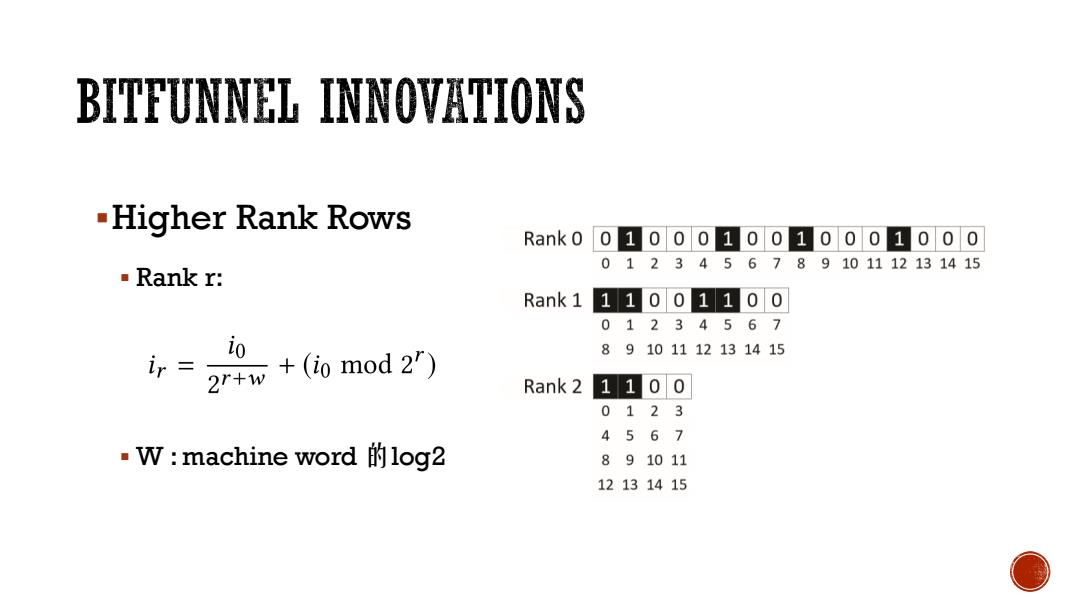
BITFUNNEL INNOVATIONS -Higher Rank Rows Rank00100010010001000 0123456789101112131415 Rank r: Rank111001100 01234567 89101112131415 ir +(io mod2) Rank 2 1100 0123 4567 .W:machine word log2 891011 12131415
Higher Rank Rows Rank r: W : machine word 的log2
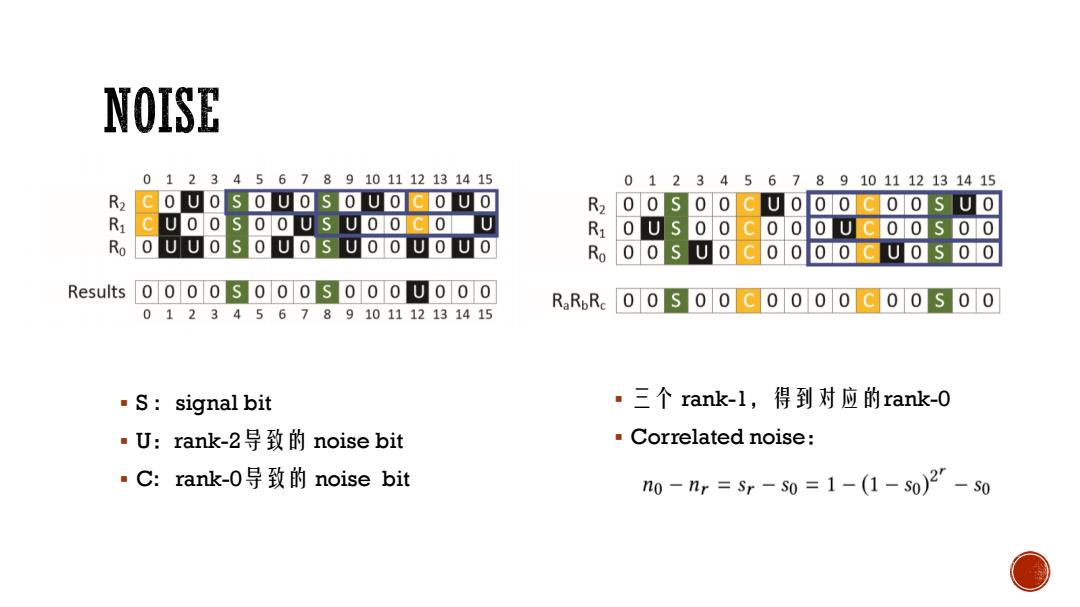
noISE 0123456789101112131415 0123456789101112131415 R2COUOSOUOS OUOCOUO R200S00CU000G00SU0 RCUOOS OOU S UOOC O U R:0Us00C000Ug00s00 RoOUUOS OUOS UO OUOUO R 00 S U O C OO 00 C UO S OO Results o 000 S O 0 O S O 0 O UO 00 RRR00500C0000C00S00 0123456789101112131415 ■S:signal bit ·三个rank-l,得到对应的rank-0 ·U:rank-2导致的noise bit .Correlated noise: ■C:rank-0导致的noise bit n0-nr=sr-s0=1-(1-50)2'-s0
S : signal bit U:rank-2导致的 noise bit C: rank-0导致的 noise bit 三 个 rank - 1,得到对应的rank - 0 Correlated noise :

BITFUNNEL INNOVATIONS -Frequency Conscious Signature ·待解决的问题:Bloom filter中每个词项固定使用k个hash ·方案:引入S,存在词项t的文档数目,s不同,使用的hash数目k不同 signal (s) hashes (k) 4) 0.1 1.954242509 0.01 2.995635195 0.001 3.999565488 0.0001 4.999956568 0.00001 5.999995657
Frequency Conscious Signature 待解决的问题:Bloom filter 中每个词项固定使用k个hash 方案:引入S,存在词项t 的文档数目,s不同,使用的hash数目k不同
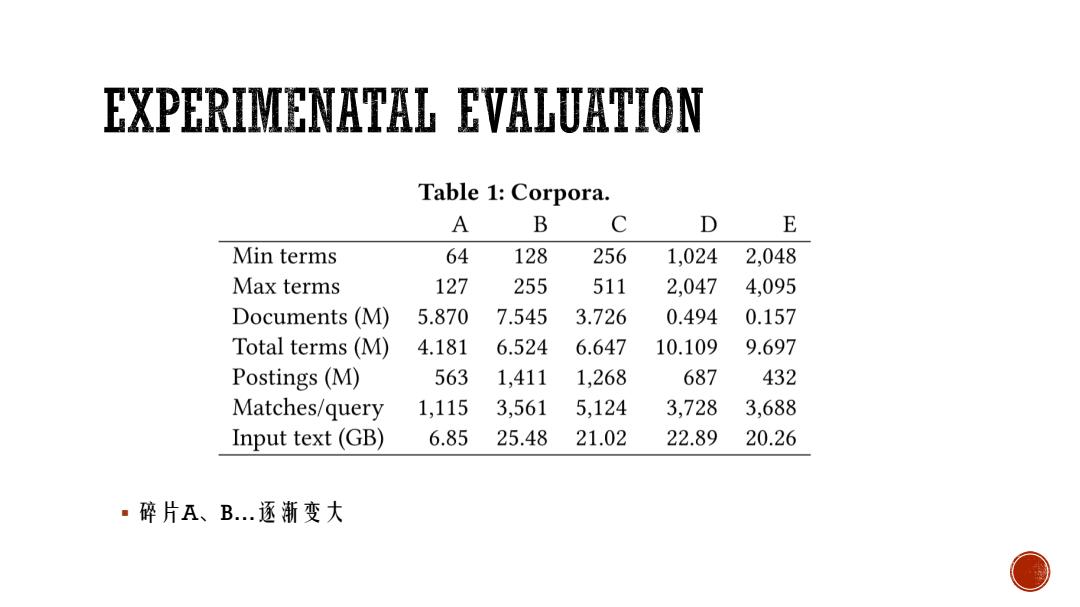
EXPERIMENATAL EVALUATION Table 1:Corpora. A B C D E Min terms 64 128 256 1,024 2,048 Max terms 127 255 511 2,047 4,095 Documents(M) 5.870 7.545 3.726 0.494 0.157 Total terms(M) 4.181 6.524 6.647 10.109 9.697 Postings (M) 563 1,411 1,268 687 432 Matches/query 1,115 3,561 5,124 3,728 3,688 Input text(GB) 6.85 25.48 21.02 22.89 20.26 ·碎片A、B..逐渐变大
碎片A、B…逐渐变大

EXPERIMENATAL EVALUATION Match Time vs.Quadwords Impact of Frequency Conscious Signatures and Higher Rank Rows Comparison with Contemporary Indexes
Match Time vs. Quadwords Impact of Frequency Conscious Signatures and Higher Rank Rows Comparison with Contemporary Indexes
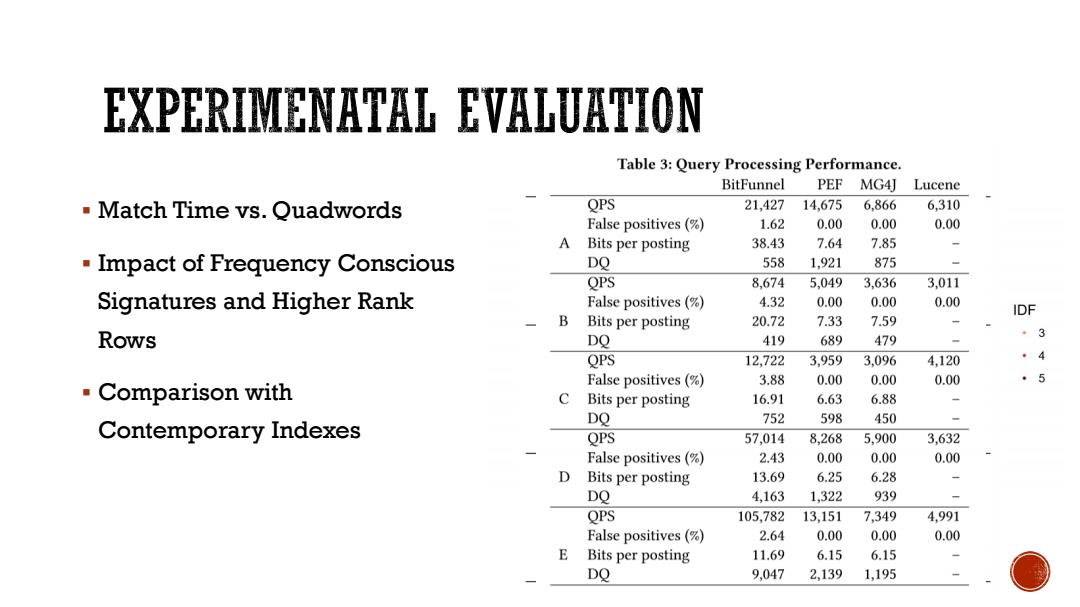
EXPERIMENATAL EVALUATION Table 3:Query Processing Performance. BitFunnel PEF MG4] Lucene Match Time vs.Quadwords QPS 21,427 14,675 6.866 6,310 False positives(%) 1.62 0.00 0.00 0.00 A Bits per posting 38.43 7.64 7.85 Impact of Frequency Conscious DQ 558 1,921 875 QPS 8,674 5,049 3,636 3,011 Signatures and Higher Rank False positives(‰) 4.32 0.00 0.00 0.00 IDF B Bits per posting 20.72 7.33 7.59 Rows DQ 419 689 479 3 QPS 12,722 3,959 3,096 4,120 。4 False positives (% 3.88 0.00 0.00 0.00 5 .Comparison with C Bits per posting 16.91 6.63 6.88 DQ 752 450 Contemporary Indexes 598 OPS 57,014 8,268 5,900 3,632 False positives (% 2.43 0.00 0.00 0.00 D Bits per posting 13.69 6.25 6.28 DQ 4,163 1,322 939 QPS 105,782 13,151 7,349 4,991 False positives(%) 2.64 0.00 0.00 0.00 Bits per posting 11.69 6.15 6.15 DQ 9,047 2,139 1,195
Match Time vs. Quadwords Impact of Frequency Conscious Signatures and Higher Rank Rows Comparison with Contemporary Indexes