
第之节 第九章 多无面数微分学的儿何应用 一元向量值函数及其导数 二、空间曲线的切线与法平面 三、曲面的切平面与法线 HIGH EDUCATION PRESS 下页返回结束
第六节 复习 目录 上页 下页 返回 结束 二、空间曲线的切线与法平面 三、曲面的切平面与法线 多元函数微分学的几何应用 第九章 一、一元向量值函数及其导数

一、一元向量值函数及其导数 (一)向量值函数的概念 (二)向量值函数的极限和连续 (三)向量值函数的导数
一、一元向量值函数及其导数 (一)向量值函数的概念 (二)向量值函数的极限和连续 (三)向量值函数的导数

>引入 空间曲线厂的参数方程 (x=o(t), y=y(t),t∈Ia,B] (z=o(t), 7=xi+可+z求ft)=p(t)i+y(t)+o(t)正 三f(t)—映射f:Ia,B]→→R3 元向量值函数
➢引入 空间曲线 Γ 的参数方程 x = (t), y = (t), z = (t), t [ , ] r = xi + yj + zk f (t) = (t)i + (t) j + (t)k r = f (t) 映射 3 f :[, ] → R 一元向量值函数

>定义 设数集DcR,则称映射:D→R"为一元向量值函数, 通常记为: 定义域 T=f(t),te D 因变量 自变量 ●注 (1)一元向量值函数是一元函数的推广 自变量 因变量 一元函数 实数值 实数值 一元向量值函数 实数值 n维向量 (2)这里只研究=3的情形
➢定义 设数集 D R, 则称映射 n f : D → R 为一元向量值函数, 通常记为: 因变量 自变量 定义域 r = f (t),t D ⚫注 (1) 一元向量值函数是一元函数的推广 一元函数 一元向量值函数 自变量 因变量 实数值 实数值 实数值 n维向量 (2) 这里只研究n=3的情形

>表示法 F(t)=f(t)i+(t)J+f(t)E,te D 或f0=(f(),f0),f3(),t∈D >图形 设广=OM,当t改变时,终点M的轨迹 (记作曲线T)称为向量值函数 7=fd),teD的终端曲线, 曲线也称为向量值函数7=ft),t∈D的图形
➢表示法 f (t) = f1 (t)i + f 2 (t) j + f 3 (t)k, t D 或 f (t) = ( f1 (t) , f 2 (t) , f 3 (t)),t D ➢图形 x y z O M r 设 r = OM , 当t 改变时,终点M的轨迹 (记作曲线 Γ) 称为向量值函数 r = f (t),t D 的终端曲线, 曲线 Γ 也称为向量值函数 r = f (t),t D 的图形 Γ

>定义设向量值函数ft)在点,的谋一去心邻域内有定义,如果 存在一个常向量,对于任意给定的正数8,总存在正数δ, 使得当1满足0<t-t,Kδ时,对应的函数值f(t)都满足: 1t)-方K8,那么,常向量方就叫做向量值函数ft)当 t→t,时的极限,记作 lim(t)=, t-tn ●注 R70=(Rf,gR0} f(t)=(f(t),f(t),f(t)),tE D
➢定义设向量值函数 f (t) 在点 0 t 的某一去心邻域内有定义, 如果 存在一个常向量 , 0 r 对于任意给定的正数 , 总存在正数 , 使得当t 满足 0 | − | 0 t t 时,对应的函数值 f (t) 都满足: | ( ) | , 0 f t − r 那么,常向量 0 r 就叫做向量值函数 f (t) 当 0 t → t 时的极限,记作 lim ( ) , 0 0 f t r t t = → ⚫注 = → → → → lim ( ) lim ( ) ,lim ( ) ,lim ( ) 1 2 3 0 0 0 0 f t f t f t f t t t t t t t t t f (t) = ( f1 (t) , f 2 (t) , f 3 (t)),t D

>定义 设向量值函数ft)在点t,的某一邻域内有定义,若 lim f(t)=f(t) t→t0 则称向量值函数ft)在t,连续 ●注向量值函数f(t)在t,连续的充要条件: ft)的三个分量函数f1(t),f2(),f(t)都在t,连续 f(t)=((t),f(t),f;(t)),t=D
➢定义 ⚫注 向量值函数 f (t) 在 0 t 连续的充要条件: 设向量值函数 f (t) 在点 0 t 的某一邻域内有定义, 若 lim ( ) ( ) 0 0 f t f t t t = → 则称向量值函数 f (t) 在 0 t 连续. f (t) 的三个分量函数 ( ), ( ), ( ) 1 2 3 f t f t f t 都在 0 t 连续. f (t) = ( f1 (t) , f 2 (t) , f 3 (t)),t D

>定义 设向量值函数ft)在点t的某一邻域内有定义,如果 ,+△)-f) △1-→0△t △t 存在,那么就称这个极限向量为向量值函数广=(t) 在处的导数或导向量,记作了(化,或 dr ●注)=f)i+f)+f). f(t)=(f(t),f,(t),f;(t)),t=D
➢定义 | . d d 0 t t t r = 设向量值函数 f (t) 在点 0 t 的某一邻域内有定义, 如果 t f t t f t t r t t + − = → → ( ) ( ) lim lim 0 0 0 0 存在,那么就称这个极限向量为向量值函数 r = f (t) 在 0 t 处的导数或导向量,记作 ( ) 0 f t 或 ⚫注 ( ) ( ) ( ) ( ) . 1 2 3 f t = f t i + f t j + f t k f (t) = ( f1 (t) , f 2 (t) , f 3 (t)),t D

>几何意义 设f(,)≠0,向量值函数r=ft),teD的终端曲线 为空间曲线T,0M=,),ON=ft,+△) 向量 指向 △7 割向量 △t>0→与t的增长方向一致 △ △t<0一→与t的增长方向相反 割向量 与t的增长方向一致 △r △7 lim 切向量 与t的增长方向一致 △1-→0△t f():向量值函数7=f),t∈D的终端曲线 厂在点M处的一个切向量,其指向与t的增长方向一致
➢几何意义 x y z O r 割向量 t 0 向量 向量值函数 r = f (t),t D 的终端曲线 为空间曲线 Γ, 割向量 切向量 与t 的增长方向一致 t 0 与t 的增长方向相反 与t 的增长方向一致 与t 的增长方向一致 向量值函数 r = f (t),t D 的终端曲线 Γ 在点M处的一个切向量,其指向与t 的增长方向一致. M N r t r t r t →0 lim( ): 0 f t ( ), 0 OM = f t ( ) 0 ON = f t + t 指向 ( ) 0, 设 f t 0
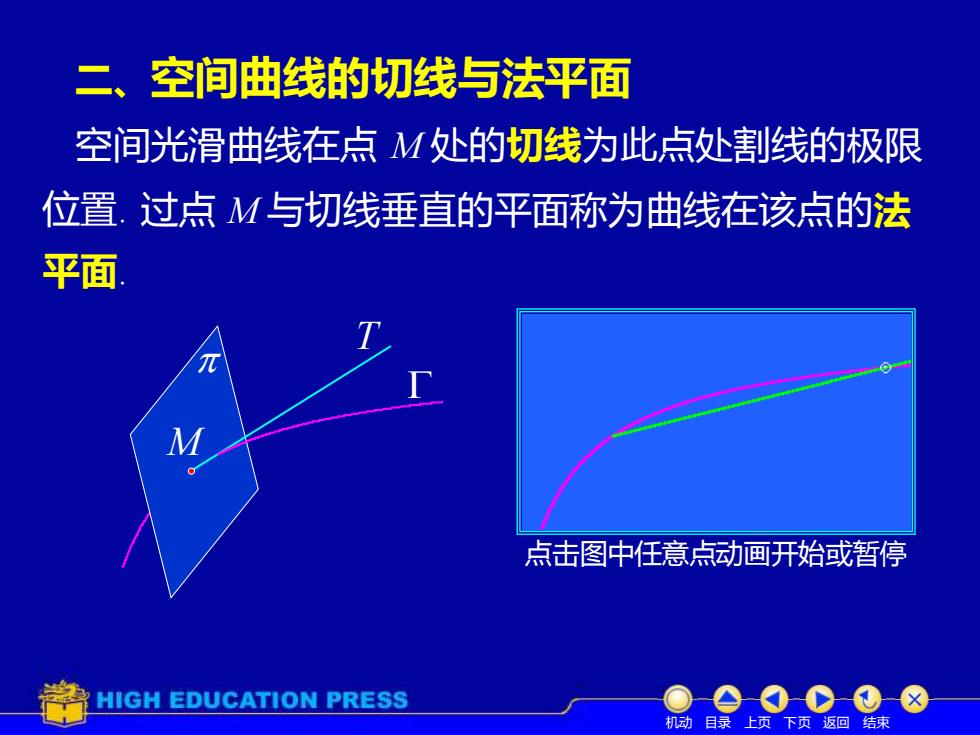
二、空间曲线的切线与法平面 空间光滑曲线在点M处的切线为此点处割线的极限 位置.过点M与切线垂直的平面称为曲线在该点的法 平面 点击图中任意点动画开始或暂停 HIGH EDUCATION PRESS 机动目录上页下页返回结束
二、空间曲线的切线与法平面 过点 M 与切线垂直的平面称为曲线在该点的法 机动 目录 上页 下页 返回 结束 位置. T M 空间光滑曲线在点 M 处的切线为此点处割线的极限 平面. 点击图中任意点动画开始或暂停