
数据科学引论-Python之道 第6课数据统计初步 一、描述性统计 我们来看看描述性统计。举个例子,如果有人问你勒布朗詹姆斯是不是一位 优秀的运动员,你该如何回答呢?也许你可以去观看他所有的比赛,但是詹姆斯 在NBA已经效力了超过13年了,他每年都要打80多场比赛,显然看完他所有 的比赛是一个不切实际的做法,那么有没有其他方式来回答这个问题呢? 有,例如我们可以用詹姆斯的场均得分来描述他的表现,这就是被称为描述 性统计,或者是总结性统计的一个例子。也就是说,我们把大量的原生数据总结 为了一个数字。詹姆斯每一场平均得分达到了27.01,他确实是一个优秀的运动 员,所以我们看到描述性统计就是要给出有关数据集的一个基本特性的描述,它 是对大样本的数据做出的一个简短总结,给出了这个数据集的一种度量。 我们怎样才能得到对数据的描述性总结呢?例如,我们可以像刚才一样,给 出平均值,也可以给出数据集的中位值或者标准差等等。不管用哪种方式来对数 据作出描述性的总结,实际上都是在对数据进行理解,探究它内在的属性和本质。 但是描述性统计也有它的局限性,例如,我们拿詹姆斯和姚明做比较,詹姆斯的 场均得分达到了27.01,而姚明的场均得分只有19分,那么是不是我们就可以 说詹姆斯是比姚明更优秀的运动员?其实很难说,为什么呢?如果我们考察不同 的维度,可以看到,詹姆斯的场均篮板只有7.2,而姚明的场均篮板数达到了9.2。 从这个方面来看,姚明的表现会显得更好,所以我们说不同的统计视角会产生不 同的结果,如果再考虑到其他的因素,比如商业市场潜力,那么这个度量就会更 加复杂,所以描述性统计具有它的局限性
数据科学引论-P瀌瀇濻瀂瀁 之道 第 6 课 数据统计初步 一、描述性统计 我们来看看描述性统计。举个例子,如果有人问你勒布朗詹姆斯是不是一位 优秀的运动员,你该如何回答呢?也许你可以去观看他所有的比赛,但是詹姆斯 在 NBA 已经效力了超过 13 年了,他每年都要打 80 多场比赛,显然看完他所有 的比赛是一个不切实际的做法,那么有没有其他方式来回答这个问题呢? 有,例如我们可以用詹姆斯的场均得分来描述他的表现,这就是被称为描述 性统计,或者是总结性统计的一个例子。也就是说,我们把大量的原生数据总结 为了一个数字。詹姆斯每一场平均得分达到了 27.01,他确实是一个优秀的运动 员,所以我们看到描述性统计就是要给出有关数据集的一个基本特性的描述,它 是对大样本的数据做出的一个简短总结,给出了这个数据集的一种度量。 我们怎样才能得到对数据的描述性总结呢?例如,我们可以像刚才一样,给 出平均值,也可以给出数据集的中位值或者标准差等等。不管用哪种方式来对数 据作出描述性的总结,实际上都是在对数据进行理解,探究它内在的属性和本质。 但是描述性统计也有它的局限性,例如,我们拿詹姆斯和姚明做比较,詹姆斯的 场均得分达到了 27.01,而姚明的场均得分只有 19 分,那么是不是我们就可以 说詹姆斯是比姚明更优秀的运动员?其实很难说,为什么呢? 如果我们考察不同 的维度,可以看到,詹姆斯的场均篮板只有 7.2,而姚明的场均篮板数达到了 9.2。 从这个方面来看,姚明的表现会显得更好,所以我们说不同的统计视角会产生不 同的结果,如果再考虑到其他的因素,比如商业市场潜力,那么这个度量就会更 加复杂,所以描述性统计具有它的局限性

如何得到一个数据集的描述性统计呢?pandas库上提供了一个叫describe 的方法,它会记自动地计算出一个数据集上的数据点的总数,也就是不包含NaN 值的所有有效的数据的个数,给出数据集的标准差四分位值,四分位值包括1/4 位值,中位值和3/4位值,还有极值也就是最大值和最小值。所有的这些统计当 中NaN的值都会被自动跳过。 df.describe() Unnamed: symboling normalized. wheel- length width height curb-weight engine. bore stroke 0 losses base size count201.000000201.000000164.000000201.000000201.000000201.000000201.000000 201.000000 201.000000201.000000201.000000 mean100.0000000.840796 122.000000 98.797015 174.20099565.88905553.766667 2555.666657126.8756223.3191543.256766 std58.1678611.254802 35.442168 6.056365 12.3221752.1014712.447822 517.29672741.5468340.2801300.316049 min0.000000-2.000000 65.000000 85.600000 141.10000060.30000047.800000 1488.00000061.0000002.5400002.070000 25%50.0000000.000000 NaN 94.500000 166.80000064.10000052.000000 2169.00000098.0000003.1500003.110000 50% 100.0000001.000000 NaN 97.000000 173.20000065.50000054.100000 2414.000000 120.0000003.310000 3.290000 75% 150.0000002.000000 NaN 102.400000 183.50000066.60000055.500000 2926.000000 141.0000003.580000 3.410000 max 200.0000003.000000 255.000000 120.900000208.10000072.000000 59.800000 4055.000000326.0000003.940000 4.170000 这是我们看到的一个例子,这张表格给出的是对汽车的一个描述。我们用26 种属性来描述汽车,每一个属性都有一定的取值范围。如果我们在样例数据集上 调用pandas的describe的方法就会得到一张表。这张表大家其实并不陌生,因 为在第四课我们讲二氧化碳排放的例子中,在加载数据以后的DataFrame上调 用describe的方法得到过类似的一个表格。 二、平均值&中位值&标准方差 最常用的刻画数据特性的指标就是算术平均值,算术平均值就是一组数字的 平均值。它的计算公式非常简单,就是将这一组数字累加以后除以数字的个数。 算术平均值描述的是数据集的集中趋势,例如,勒布朗詹姆斯有的时候发挥欠佳, 他的得分比较少,就是用红颜色表示的在数轴左侧的数据,但在有些场次他的发 挥又超常,得分非常高,就是用绿颜色表示的在数轴右侧的数据。在大多数情况 下,他发挥正常,也就是在数轴中间这一组用蓝色表示的数据
如何得到一个数据集的描述性统计呢?瀃濴瀁濷濴瀆 库上提供了一个叫 濷濸瀆濶瀅濼濵濸 的方法,它会记自动地计算出一个数据集上的数据点的总数,也就是不包含 N濴N 值的所有有效的数据的个数,给出数据集的标准差四分位值,四分位值包括 1/4 位值,中位值和 3/4 位值,还有极值也就是最大值和最小值。所有的这些统计当 中 N濴N 的值都会被自动跳过。 这是我们看到的一个例子,这张表格给出的是对汽车的一个描述。我们用 26 种属性来描述汽车,每一个属性都有一定的取值范围。如果我们在样例数据集上 调用 瀃濴瀁濷濴瀆 的 濷濸瀆濶瀅濼濵濸 的方法就会得到一张表。这张表大家其实并不陌生,因 为在第四课我们讲二氧化碳排放的例子中,在加载数据以后的 D濴瀇濴F瀅濴瀀濸 上调 用 濷濸瀆濶瀅濼濵濸 的方法得到过类似的一个表格。 二、平均值&中位值&标准方差 最常用的刻画数据特性的指标就是算术平均值,算术平均值就是一组数字的 平均值。它的计算公式非常简单,就是将这一组数字累加以后除以数字的个数。 算术平均值描述的是数据集的集中趋势,例如,勒布朗詹姆斯有的时候发挥欠佳, 他的得分比较少,就是用红颜色表示的在数轴左侧的数据,但在有些场次他的发 挥又超常,得分非常高,就是用绿颜色表示的在数轴右侧的数据。在大多数情况 下,他发挥正常,也就是在数轴中间这一组用蓝色表示的数据

文=∑资=1xn(x1++xw) -●●● 如果我们对所有的数据求平均值,就会得到一个基本上位于发挥正常的这个 区间当中的一个值,它刻画了詹姆斯每一场得分的一个集中趋势。在pandas上 计算平均值会非常简单,在组装好的DataFrame对象上调用mean函数就会得 到每一列上面的平均值。 import pandas as pd df=pd.DataFrame('c1':【1,2,3],'c2':[1,2,100],'c3':[100,200,300]},index-=['a','b','e]) df.head() c1 c2 c3 a1 100 b22 200 c3100300 df.mean() cl 2,000000 34,333333 200.000000 dtype:float64 平均值有一些问题,让我们通过一个例子来说明。假设我们想计算正在一家 正餐厅就餐的人群的平均收入,如果现在有十位顾客,每一位顾客的收入都是1 万美元,我们求平均值就会得到人均收入就是1万美元。这时候1万美元这个数 字就准确客观地刻画了在这家餐厅中正在就餐的顾客的净资产。但是如果这个时 候比尔盖茨走进了一家饭店,那么由于他的身家达到了856亿美元,所以他一个 人就会将整个餐厅当中的人均收入拉高到将近80亿美元,显然对于这家餐厅来 说,80亿美元的人均收入并不具备代表性,也就是说,我们需要一种新的用来 度量数据分布的中间值的方法。 这时就可以用到中位值。中位值作为一种度量数据分布的中间值的方法,对
如果我们对所有的数据求平均值,就会得到一个基本上位于发挥正常的这个 区间当中的一个值,它刻画了詹姆斯每一场得分的一个集中趋势。在 瀃濴瀁濷濴瀆 上 计算平均值会非常简单,在组装好的 D濴瀇濴F瀅濴瀀濸 对象上调用 瀀濸濴瀁 函数就会得 到每一列上面的平均值。 平均值有一些问题,让我们通过一个例子来说明。假设我们想计算正在一家 正餐厅就餐的人群的平均收入,如果现在有十位顾客,每一位顾客的收入都是 1 万美元,我们求平均值就会得到人均收入就是 1 万美元。这时候 1 万美元这个数 字就准确客观地刻画了在这家餐厅中正在就餐的顾客的净资产。但是如果这个时 候比尔盖茨走进了一家饭店,那么由于他的身家达到了 856 亿美元,所以他一个 人就会将整个餐厅当中的人均收入拉高到将近 80 亿美元,显然对于这家餐厅来 说,80 亿美元的人均收入并不具备代表性,也就是说,我们需要一种新的用来 度量数据分布的中间值的方法。 这时就可以用到中位值。中位值作为一种度量数据分布的中间值的方法,对

于一组数字来说,中位值就是有一半的数字小于它,另外一半数字大于它的那个 数字。例如,在包含奇数个数字的集合中,中位值就是将这一组数字从小到大排 列好,位于最中间的数字,而在包含偶数个数字的集合中,中位值是将这一组数 据从小到大排列好之后,位于最中间的两个数据的平均值。 中位数有什么好处呢?当数据当中出现离群值时,它能够更准确地刻画数据 的集中趋势。例如,对于包含100、4、2、1、7这五个元素数据集,其中有四个 数据都是小于10的,只有一个数据是远远大于10的100,那么一百就是一个离 群值。我们把这组数字从小到大排列之后,中位置就是位于最中间的4。很显然, 4准确地刻画▣了这一组数据的集中趋势。 平均值和中位值描述的都是数据集的集中趋势,如果数据是对称的,也就是 说在数据集当中没有离群值,那么平均值和中位置就基本相同。但是当数据集中 出现离群值时,它会显着地改变平均值,但是对中位值的影响要小得多。例如, 在前面的餐厅例子中,由于比尔盖茨走进了餐厅,他把平均值显著地抬高了,得 到的人均收入达到了近80亿美元。但是,他走进这家餐厅之后,数据集的中位 值仍然是1万美元,相对于80亿美元来说,1万美元更准确地刻画了这11位用 户的数据的集中趋势,所以在这个时候我们看到中位置要优于平均值。我们看到 80亿美元这个值比1万美元这个值要差很多,也就是说,对于这个例子而言,1 万美元的中位值是对餐厅人群净资产的一种更好的表示形式。在pandas库中, 计算中位置也很简单,在组装好的DataFrame对象上调用median方法,它就会 对每一列的数据计算中位值。我们现在来观察C2这一列,它包含一个离群值100 但是中位值计算出来是20,就比前面我们用平均值计算时C2这一列的平均值 34.333333要准确得多,也就更好地反映了C2这一列的数据的集中趋势
于一组数字来说,中位值就是有一半的数字小于它,另外一半数字大于它的那个 数字。例如,在包含奇数个数字的集合中,中位值就是将这一组数字从小到大排 列好,位于最中间的数字,而在包含偶数个数字的集合中,中位值是将这一组数 据从小到大排列好之后,位于最中间的两个数据的平均值。 中位数有什么好处呢?当数据当中出现离群值时,它能够更准确地刻画数据 的集中趋势。例如,对于包含 100、4、2、1、7 这五个元素数据集,其中有四个 数据都是小于 10 的,只有一个数据是远远大于 10 的 100,那么一百就是一个离 群值。我们把这组数字从小到大排列之后,中位置就是位于最中间的 4。很显然, 4 准确地刻画了这一组数据的集中趋势。 平均值和中位值描述的都是数据集的集中趋势,如果数据是对称的,也就是 说在数据集当中没有离群值,那么平均值和中位置就基本相同。但是当数据集中 出现离群值时,它会显着地改变平均值,但是对中位值的影响要小得多。例如, 在前面的餐厅例子中,由于比尔盖茨走进了餐厅,他把平均值显著地抬高了,得 到的人均收入达到了近 80 亿美元。但是,他走进这家餐厅之后,数据集的中位 值仍然是 1 万美元,相对于 80 亿美元来说,1 万美元更准确地刻画了这 11 位用 户的数据的集中趋势,所以在这个时候我们看到中位置要优于平均值。我们看到 80 亿美元这个值比 1 万美元这个值要差很多,也就是说,对于这个例子而言,1 万美元的中位值是对餐厅人群净资产的一种更好的表示形式。在 瀃濴瀁濷濴瀆 库中, 计算中位置也很简单,在组装好的 D濴瀇濴F瀅濴瀀濸 对象上调用 瀀濸濷濼濴瀁 方法,它就会 对每一列的数据计算中位值。我们现在来观察 C2 这一列,它包含一个离群值 100, 但是中位值计算出来是 2.0,就比前面我们用平均值计算时 C2 这一列的平均值 34.333333 要准确得多,也就更好地反映了 C2 这一列的数据的集中趋势

import pandas as pd df=pd.DataFrame({'c1':【1,2,3],c2':【1,2,100],'c3:[100,200,300】J,index=['a',"b','c']) df.head() c1 c2 c3 a11100 b22200 c3100300 df.median() cl 2.0 c2 2.0 c3 200.0 dtype:float64 平均值的另一个问题靠样本方差来解决,这个问题是什么呢?我们举一个例 子,现在有两组人,他们的体重数据分别是在下面表示的这八个数据。 A 150 152 148 150 B 9 8 292291 可以看到,对于第一组人来说,他们的体重比较接近,而对于第二组人来说 他们体重的差异非常大,但是如果我们用平均值来表示,就会发现这两组人的平 均体重都是150,用平均值是无法体现出这两组人明显的这种差异性,样本方差 可以帮助我们来区分这两组人的差异,样本方差度量的是数据的分布范围。它的 计算方式是先计算出两组数据的平均值,然后将数据中每一个数字都和这个平均 值进行比较,他们的差的平方累加起来以后再除以数据的个数就是方差。 N SN(x) = (xn-)2 n=1
平均值的另一个问题靠样本方差来解决,这个问题是什么呢?我们举一个例 子,现在有两组人,他们的体重数据分别是在下面表示的这八个数据。 可以看到,对于第一组人来说,他们的体重比较接近,而对于第二组人来说, 他们体重的差异非常大,但是如果我们用平均值来表示,就会发现这两组人的平 均体重都是 150,用平均值是无法体现出这两组人明显的这种差异性,样本方差 可以帮助我们来区分这两组人的差异,样本方差度量的是数据的分布范围。它的 计算方式是先计算出两组数据的平均值,然后将数据中每一个数字都和这个平均 值进行比较,他们的差的平方累加起来以后再除以数据的个数就是方差

举例来说,对于刚才体重差异较大的一组人而言,他们的方差就分别是9, 8,291和292,与平均值150的差的平方累加以后再除以数据的个数4得到的 值就是20022.5。而对于体重比较接近的一组选手而言,他们的方差是分别是148, 152、150和150,与平均值150的差的平方累加以后再除以数据的个数4得到 的方差就是2。很显然,这两组人的方差的差异非常大,尽管他们的平均值相同。 通过方差我们就可以看出这两组数据不同的特性。方差越小,说明所有的数据的 分布范围越小,它们更接近于平均值,而方差越大,说明数据的分布范围越大, 它们更远离平均值。跟方差密切关联的另外一个指标是标准差,标准差就是对方 差的开方。在pandas中计算标准差的方式是在组装好的DataFrame对象上调用 std这个函数,它会计算每一列数据的标准差。 import pandas as pd df=pd.DataFrame({'c1:【1,2,3],c2':【1,2,100],'c3':l100,200,300】J,index=a',b',c'1) df.head() c1c2 c3 a11100 b22200 c3100300 df.std() 2 1.0000 56.8712 3 100.0000 dtype:float64 三、直方图&箱线图 直方图是一种常见的数据统计工具,用来计算对象的实例个数。例如,在下 面这个数据集中,这9个数据有三种不同的取值,分别是黄、红、绿。于是,我 们计算不同取值的实例的个数,得到了2个黄的,4个红的,以及3个绿的这样 的数据集,这就是最简单的直方图
举例来说,对于刚才体重差异较大的一组人而言,他们的方差就分别是 9, 8,291 和 292,与平均值 150 的差的平方累加以后再除以数据的个数 4 得到的 值就是 20022.5。而对于体重比较接近的一组选手而言,他们的方差是分别是 148, 152、150 和 150,与平均值 150 的差的平方累加以后再除以数据的个数 4 得到 的方差就是 2。很显然,这两组人的方差的差异非常大,尽管他们的平均值相同。 通过方差我们就可以看出这两组数据不同的特性。方差越小,说明所有的数据的 分布范围越小,它们更接近于平均值,而方差越大,说明数据的分布范围越大, 它们更远离平均值。跟方差密切关联的另外一个指标是标准差,标准差就是对方 差的开方。在 瀃濴瀁濷濴瀆 中计算标准差的方式是在组装好的 D濴瀇濴F瀅濴瀀濸 对象上调用 瀆瀇濷 这个函数,它会计算每一列数据的标准差。 三、直方图&箱线图 直方图是一种常见的数据统计工具,用来计算对象的实例个数。例如,在下 面这个数据集中,这 9 个数据有三种不同的取值,分别是黄、红、绿。于是,我 们计算不同取值的实例的个数,得到了 2 个黄的,4 个红的,以及 3 个绿的这样 的数据集,这就是最简单的直方图

在pandas中绘制直方图的方式很简单,只需要在装载好的DataFrame对象 上调用hist方法。例如,我们可以看到这个DataFrame包含C1和C2两列,这 两列完全由数字构成,所以在这个DataFrame上调用了hist方法之后,就会针 对这两列画出两个直方图,每一个直方图对应其中一列,表示了这一列中不同取 值的数据的个数。 c1 c2 df.hist() 11 array([[, 21 ]],dtype=object) 31 cl 42 6 93 5 第二种常见的数据统计工具是箱线图。箱线图稍显复杂一些,它由一个方框 以及纵向贯穿它的竖线构成,这个方框的最下部表示数据的下四分位数,顶部表 示它的上四分位数,方框的范围就表达了四分位数的取值范围。在方框的中部有 一条贯穿方框的横线,表达的是整个数据集的中位值。在这条贯穿方框的纵线上, 上边缘表示的是整个数据集的最大值,下边缘表示的数据集的最小值。在方框中
在 瀃濴瀁濷濴瀆 中绘制直方图的方式很简单,只需要在装载好的 D濴瀇濴F瀅濴瀀濸 对象 上调用 濻濼瀆瀇 方法。例如,我们可以看到这个 D濴瀇濴F瀅濴瀀濸 包含 C1 和 C2 两列,这 两列完全由数字构成,所以在这个 D濴瀇濴F瀅濴瀀濸 上调用了 濻濼瀆瀇 方法之后,就会针 对这两列画出两个直方图,每一个直方图对应其中一列,表示了这一列中不同取 值的数据的个数。 第二种常见的数据统计工具是箱线图。箱线图稍显复杂一些,它由一个方框 以及纵向贯穿它的竖线构成,这个方框的最下部表示数据的下四分位数,顶部表 示它的上四分位数,方框的范围就表达了四分位数的取值范围。在方框的中部有 一条贯穿方框的横线,表达的是整个数据集的中位值。在这条贯穿方框的纵线上, 上边缘表示的是整个数据集的最大值,下边缘表示的数据集的最小值。在方框中
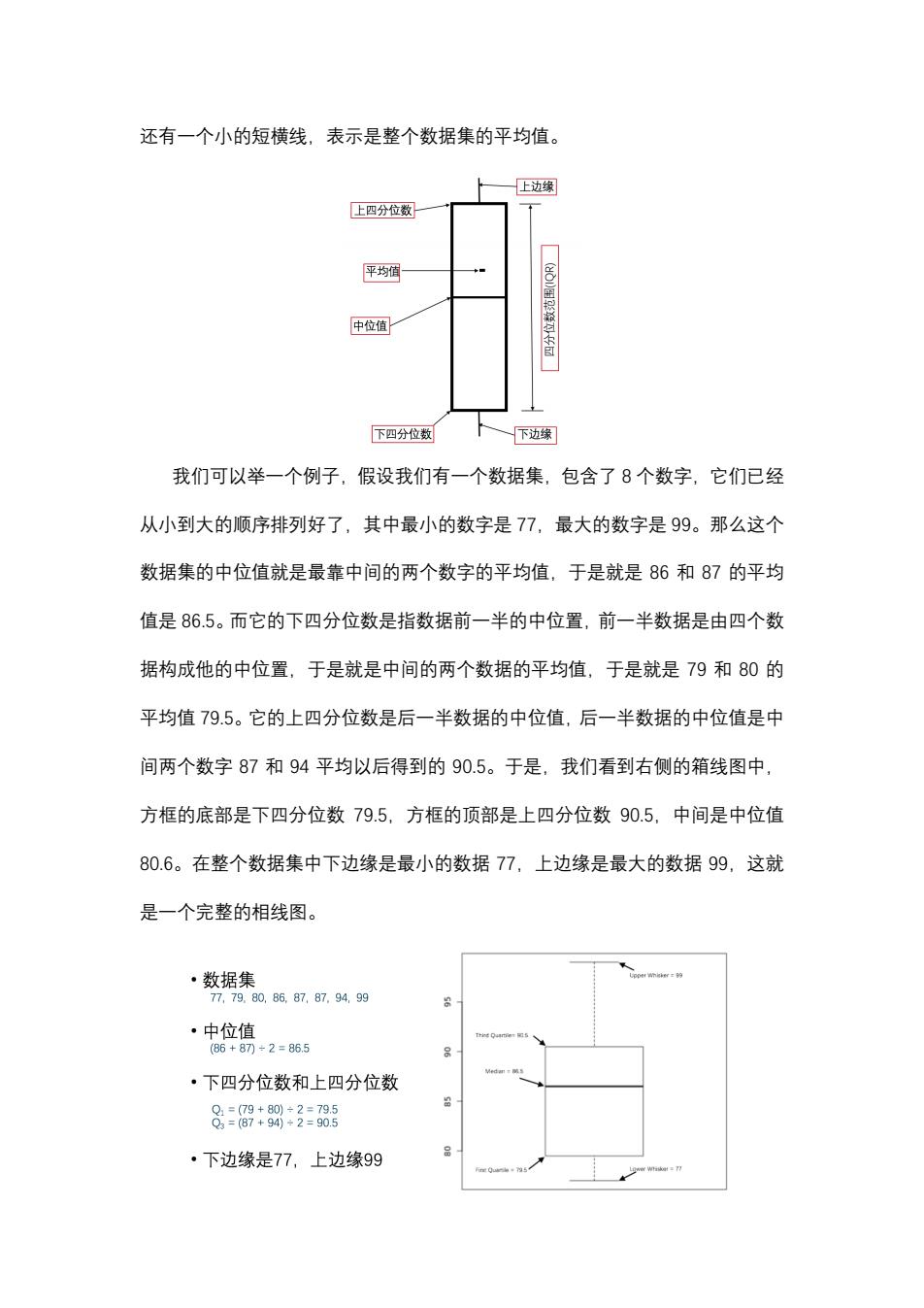
还有一个小的短横线,表示是整个数据集的平均值。 上边缘 上四分位数 平均值 中位值 下四分位数 下边缘 我们可以举一个例子,假设我们有一个数据集,包含了8个数字,它们已经 从小到大的顺序排列好了,其中最小的数字是77,最大的数字是99。那么这个 数据集的中位值就是最靠中间的两个数字的平均值,于是就是86和87的平均 值是86.5。而它的下四分位数是指数据前一半的中位置,前一半数据是由四个数 据构成他的中位置,于是就是中间的两个数据的平均值,于是就是79和80的 平均值79.5。它的上四分位数是后一半数据的中位值,后一半数据的中位值是中 间两个数字87和94平均以后得到的90.5。于是,我们看到右侧的箱线图中, 方框的底部是下四分位数79.5,方框的顶部是上四分位数90.5,中间是中位值 80.6。在整个数据集中下边缘是最小的数据77,上边缘是最大的数据99,这就 是一个完整的相线图。 ·数据集 77,79.80,8687,87.94.99 ·中位值 (86+87)+2=86.5 ·下四分位数和上四分位数 8=89+8*子:8 ·下边缘是77,上边缘99
还有一个小的短横线,表示是整个数据集的平均值。 我们可以举一个例子,假设我们有一个数据集,包含了 8 个数字,它们已经 从小到大的顺序排列好了,其中最小的数字是 77,最大的数字是 99。那么这个 数据集的中位值就是最靠中间的两个数字的平均值,于是就是 86 和 87 的平均 值是 86.5。而它的下四分位数是指数据前一半的中位置,前一半数据是由四个数 据构成他的中位置,于是就是中间的两个数据的平均值,于是就是 79 和 80 的 平均值 79.5。它的上四分位数是后一半数据的中位值,后一半数据的中位值是中 间两个数字 87 和 94 平均以后得到的 90.5。于是,我们看到右侧的箱线图中, 方框的底部是下四分位数 79.5,方框的顶部是上四分位数 90.5,中间是中位值 80.6。在整个数据集中下边缘是最小的数据 77,上边缘是最大的数据 99,这就 是一个完整的相线图
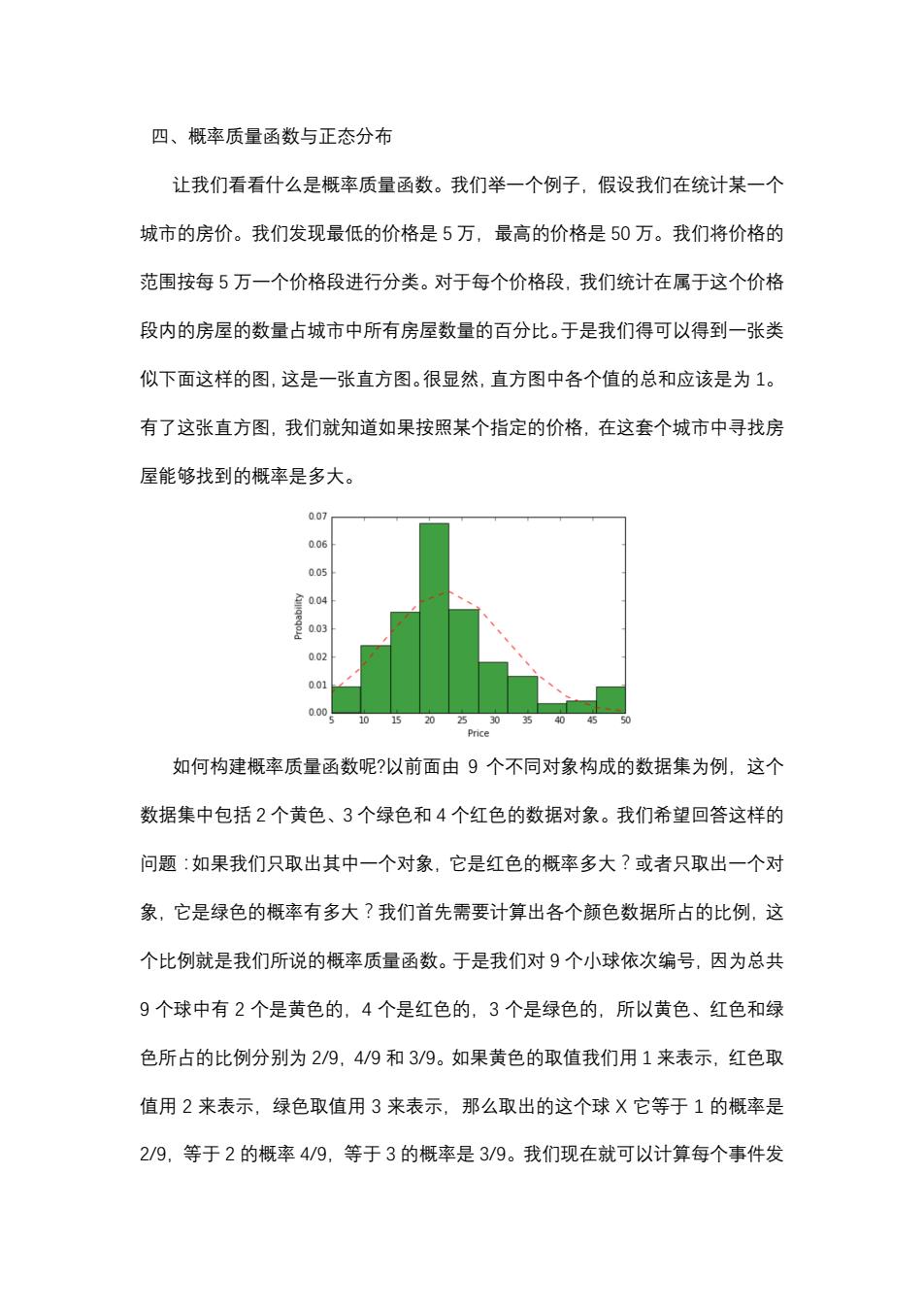
四、概率质量函数与正态分布 让我们看看什么是概率质量函数。我们举一个例子,假设我们在统计某一个 城市的房价。我们发现最低的价格是5万,最高的价格是50万。我们将价格的 范围按每5万一个价格段进行分类。对于每个价格段,我们统计在属于这个价格 段内的房屋的数量占城市中所有房屋数量的百分比。于是我们得可以得到一张类 似下面这样的图,这是一张直方图。很显然,直方图中各个值的总和应该是为1。 有了这张直方图,我们就知道如果按照某个指定的价格,在这套个城市中寻找房 屋能够找到的概率是多大。 0.07 006 0.05 室0.04 0.03 0.02 0.01 0.00 10 15 20 2530 5 40 Price 如何构建概率质量函数呢?以前面由9个不同对象构成的数据集为例,这个 数据集中包括2个黄色、3个绿色和4个红色的数据对象。我们希望回答这样的 问题:如果我们只取出其中一个对象,它是红色的概率多大?或者只取出一个对 象,它是绿色的概率有多大?我们首先需要计算出各个颜色数据所占的比例,这 个比例就是我们所说的概率质量函数。于是我们对9个小球依次编号,因为总共 9个球中有2个是黄色的,4个是红色的,3个是绿色的,所以黄色、红色和绿 色所占的比例分别为2/9,4/9和3/9。如果黄色的取值我们用1来表示,红色取 值用2来表示,绿色取值用3来表示,那么取出的这个球X它等于1的概率是 2/9,等于2的概率4/9,等于3的概率是3/9。我们现在就可以计算每个事件发
四、概率质量函数与正态分布 让我们看看什么是概率质量函数。我们举一个例子,假设我们在统计某一个 城市的房价。我们发现最低的价格是 5 万,最高的价格是 50 万。我们将价格的 范围按每 5 万一个价格段进行分类。对于每个价格段,我们统计在属于这个价格 段内的房屋的数量占城市中所有房屋数量的百分比。于是我们得可以得到一张类 似下面这样的图,这是一张直方图。很显然,直方图中各个值的总和应该是为 1。 有了这张直方图,我们就知道如果按照某个指定的价格,在这套个城市中寻找房 屋能够找到的概率是多大。 如何构建概率质量函数呢?以前面由 9 个不同对象构成的数据集为例,这个 数据集中包括 2 个黄色、3 个绿色和 4 个红色的数据对象。我们希望回答这样的 问题:如果我们只取出其中一个对象,它是红色的概率多大?或者只取出一个对 象,它是绿色的概率有多大?我们首先需要计算出各个颜色数据所占的比例,这 个比例就是我们所说的概率质量函数。于是我们对 9 个小球依次编号,因为总共 9 个球中有 2 个是黄色的,4 个是红色的,3 个是绿色的,所以黄色、红色和绿 色所占的比例分别为 2/9,4/9 和 3/9。如果黄色的取值我们用 1 来表示,红色取 值用 2 来表示,绿色取值用 3 来表示,那么取出的这个球 X 它等于 1 的概率是 2/9,等于 2 的概率 4/9,等于 3 的概率是 3/9。我们现在就可以计算每个事件发

生的概率了。 4 4 9 3 9 3-92-9 2-9 1-9 8 2 3 A 我们看到的概率质量函数和前面表示概率质量函数的直方图都有一个限制, 即,在图中我们看到的X的取值只能是离散的值,就像刚才我们看到的1、2、 3。但是,在很多情况下,我们实际的取值是实数,这也就意味着我们的取值可 能不是几个简单的离散值,而是在光滑的数轴上任意一个位置都可能出现的取值。 例如,我们的速度可以是4公里/每小时,也可以是4.5公里/每小时,或者是在 介于这两者之间的任意一个速度。再例如,我们每天要喝1公斤水或者2.5公斤 水,或者是介于这两个值之间的任意一个数量的水。 在这种情况下,用离散值表达的直方图和概率质量函数就有些不适用了,这 时候我们可以使用概率密度函数。在概率密度函数中,X可以是实数,也就是说, 将其在坐标系中画出来是一条光滑连续的曲线,而不是几个离散的点的取值。概 率密度函数有很多种,马上我们会讨论的是其中一种最常用的,叫做正态分布的 密度函数。由于概率密度函数是光滑连续的曲线,所以当我们在预测某个事件的 取值范围位于A和B之间时,实际上它的概率就是在A和B这个取值范围内计 算这条曲线围成的面积,也就是说对这条曲线在A到B的范围内做积分
生的概率了。 我们看到的概率质量函数和前面表示概率质量函数的直方图都有一个限制, 即,在图中我们看到的 X 的取值只能是离散的值,就像刚才我们看到的 1、2、 3。但是,在很多情况下,我们实际的取值是实数,这也就意味着我们的取值可 能不是几个简单的离散值,而是在光滑的数轴上任意一个位置都可能出现的取值。 例如,我们的速度可以是 4 公里/每小时,也可以是 4.5 公里/每小时,或者是在 介于这两者之间的任意一个速度。再例如,我们每天要喝 1 公斤水或者 2.5 公斤 水,或者是介于这两个值之间的任意一个数量的水。 在这种情况下,用离散值表达的直方图和概率质量函数就有些不适用了,这 时候我们可以使用概率密度函数。在概率密度函数中,X 可以是实数,也就是说, 将其在坐标系中画出来是一条光滑连续的曲线,而不是几个离散的点的取值。概 率密度函数有很多种,马上我们会讨论的是其中一种最常用的,叫做正态分布的 密度函数。由于概率密度函数是光滑连续的曲线,所以当我们在预测某个事件的 取值范围位于 A 和 B 之间时,实际上它的概率就是在 A 和 B 这个取值范围内计 算这条曲线围成的面积,也就是说对这条曲线在 A 到 B 的范围内做积分