
数据科学引论-Python之道 第9课机器学习 一、概述 今天我们来学习有关机器学习的知识。首先,我们先来看两个例子,第一个 是snapchat,.这是一款由斯坦福的大学生开发的社交类的APP,用户通过这个 APP可以互相分享照片,在接收到发送过来的照片之后,还可以做一些像面部识 别的事情,以此来实现一些比较有趣的功能。例如,揭示照片中人物的心情到底 是高兴还是沮丧。照片被阅读之后会被自动地销毁掉,这是一款非常出名的阅后 即焚的应用。第二个例子是微软的Kbox Kinect,这是一种动作捕捉的外设,它 捕捉了我们的动作之后,可以将我们的动作融入到游戏中去,从而提高了游戏者 的用户体验。这两个例子都频繁或者深度地使用了机器学习技术。在整个数据分 析的过程中,无论是在分析方法的选择还是在业务建模这两个步骤的哪一个,都 可以深度地使用或者是选择机器学习方法。 机器学习主要的分析方法和算法罗列如下: 第一是关联分析,也就是要找到数据集之间的频繁共现项,以此来发现数据 集之间的关联关系,常用的有Apriori关联规则这样的算法。 第二是分类,也就是要对数据集进行分类,例如,我们在事物类别预测上可 以用到这样的方法,具体的算法有各种各样的决策树、分类回归树、支持向量机、 神经网络、朴素贝叶斯和卡方自动交叉检验等。 第三是评估预测方法,例如用来预测连续值的各种各样的回归算法、支持向 量机和K近邻算法。 第四是聚类,也就是将数据集划分成若干个等价类,使得在这些聚集好的类
数据科学引论-P瀌瀇濻瀂瀁 之道 第 9 课 机器学习 一、概述 今天我们来学习有关机器学习的知识。首先,我们先来看两个例子,第一个 是 瀆瀁濴瀃濶濻濴瀇,这是一款由斯坦福的大学生开发的社交类的 APP,用户通过这个 APP 可以互相分享照片,在接收到发送过来的照片之后,还可以做一些像面部识 别的事情,以此来实现一些比较有趣的功能。例如,揭示照片中人物的心情到底 是高兴还是沮丧。照片被阅读之后会被自动地销毁掉,这是一款非常出名的阅后 即焚的应用。第二个例子是微软的 X濵瀂瀋 K濼瀁濸濶瀇,这是一种动作捕捉的外设,它 捕捉了我们的动作之后,可以将我们的动作融入到游戏中去,从而提高了游戏者 的用户体验。这两个例子都频繁或者深度地使用了机器学习技术。在整个数据分 析的过程中,无论是在分析方法的选择还是在业务建模这两个步骤的哪一个,都 可以深度地使用或者是选择机器学习方法。 机器学习主要的分析方法和算法罗列如下: 第一是关联分析,也就是要找到数据集之间的频繁共现项,以此来发现数据 集之间的关联关系,常用的有 A瀃瀅濼瀂瀅濼 关联规则这样的算法。 第二是分类,也就是要对数据集进行分类,例如,我们在事物类别预测上可 以用到这样的方法,具体的算法有各种各样的决策树、分类回归树、支持向量机、 神经网络、朴素贝叶斯和卡方自动交叉检验等。 第三是评估预测方法,例如用来预测连续值的各种各样的回归算法、支持向 量机和 K 近邻算法。 第四是聚类,也就是将数据集划分成若干个等价类,使得在这些聚集好的类

的内部的数据彼此之间比较相似,而类之间的数据差异比较大,常用的算法有K 均值和分层聚类方法。 第五是序列模式挖掘,就是按照时间发生的顺序对一系列的事件进行挖掘, 例如,我们想分析某个网页或者是某个视频被浏览和观看的模型,常用的算法有 马尔可夫模型和隐马尔可夫模型。 第六是降维,当问题特别复杂时,我们是难以对其进行处理的,所以我们希 望通过降维来降低问题的复杂性,从而解决问题,主要使用的方法有主成分分析。 第七是可视化,就像我们前面课中所提到的,数据可视化之后,可以方便人 们对数据的理解,更容易产生对数据的洞察。 第八是概括,也就是对数据集产生概括性的描述。之前我们提到的在 DataFrame上调用describe方法就可以得到所有数值型列的统计数据,包括最 大值、最小值、平均值、中位值等等。 第九是偏差检测,也就要找到一系列数据集中的数据变点,例如,在拟合一 条符合正关联或负关联的直线时,我们总会发现有一些点会远离这条直线,这些 点就属于变点。 最后是链接或者是图分析。如果把节点之间的链接关系画出来也是一张图, 所以它们本质是一样的,就是通过对图的分析来发现一些数据之间的关联关系。 机器学习领域非常广泛,本节课将挑选其中几种加以描述,并通过notebook 让大家掌握在Python框架下如何使用它们。 二、预测 下面让我们来看看预测方法。我们举一个例子,假设我们想根据一辆汽车的 各项技术指标来预测它的二氧化碳的排放量,那么我们该怎么做呢?
的内部的数据彼此之间比较相似,而类之间的数据差异比较大,常用的算法有 K 均值和分层聚类方法。 第五是序列模式挖掘,就是按照时间发生的顺序对一系列的事件进行挖掘, 例如,我们想分析某个网页或者是某个视频被浏览和观看的模型,常用的算法有 马尔可夫模型和隐马尔可夫模型。 第六是降维,当问题特别复杂时,我们是难以对其进行处理的,所以我们希 望通过降维来降低问题的复杂性,从而解决问题,主要使用的方法有主成分分析。 第七是可视化,就像我们前面课中所提到的,数据可视化之后,可以方便人 们对数据的理解,更容易产生对数据的洞察。 第八是概括,也就是对数据集产生概括性的描述。之前我们提到的在 D濴瀇濴F瀅濴瀀濸 上调用 濷濸瀆濶瀅濼濵濸 方法就可以得到所有数值型列的统计数据,包括最 大值、最小值、平均值、中位值等等。 第九是偏差检测,也就要找到一系列数据集中的数据变点,例如,在拟合一 条符合正关联或负关联的直线时,我们总会发现有一些点会远离这条直线,这些 点就属于变点。 最后是链接或者是图分析。如果把节点之间的链接关系画出来也是一张图, 所以它们本质是一样的,就是通过对图的分析来发现一些数据之间的关联关系。 机器学习领域非常广泛,本节课将挑选其中几种加以描述,并通过 瀁瀂瀇濸濵瀂瀂濾 让大家掌握在 P瀌瀇濻瀂瀁 框架下如何使用它们。 二、预测 下面让我们来看看预测方法。我们举一个例子,假设我们想根据一辆汽车的 各项技术指标来预测它的二氧化碳的排放量,那么我们该怎么做呢?
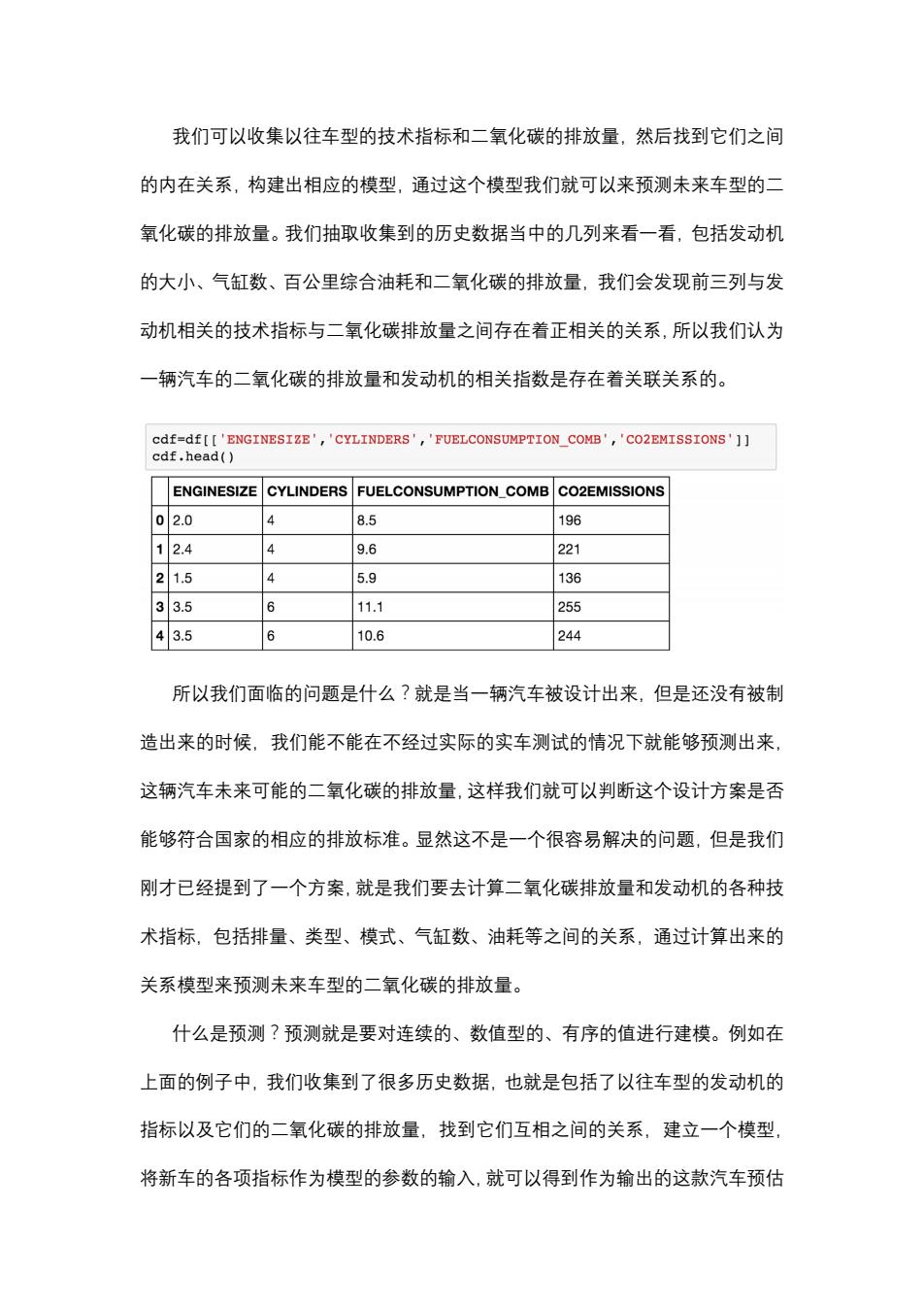
我们可以收集以往车型的技术指标和二氧化碳的排放量,然后找到它们之间 的内在关系,构建出相应的模型,通过这个模型我们就可以来预测未来车型的二 氧化碳的排放量。我们抽取收集到的历史数据当中的几列来看一看,包括发动机 的大小、气缸数、百公里综合油耗和二氧化碳的排放量,我们会发现前三列与发 动机相关的技术指标与二氧化碳排放量之间存在着正相关的关系,所以我们认为 一辆汽车的二氧化碳的排放量和发动机的相关指数是存在着关联关系的。 cdf=df[['ENGINESIZE','CYLINDERS','FUELCONSUMPTION_COMB','CO2EMISSIONS'] cdf.head() ENGINESIZE CYLINDERS FUELCONSUMPTION COMBCO2EMISSIONS 02.0 4 8.5 196 12.4 4 9.6 221 21.5 4 5.9 136 33.5 6 11.1 255 43.5 6 10.6 244 所以我们面临的问题是什么?就是当一辆汽车被设计出来,但是还没有被制 造出来的时候,我们能不能在不经过实际的实车测试的情况下就能够预测出来, 这辆汽车未来可能的二氧化碳的排放量,这样我们就可以判断这个设计方案是否 能够符合国家的相应的排放标准。显然这不是一个很容易解决的问题,但是我们 刚才已经提到了一个方案,就是我们要去计算二氧化碳排放量和发动机的各种技 术指标,包括排量、类型、模式、气缸数、油耗等之间的关系,通过计算出来的 关系模型来预测未来车型的二氧化碳的排放量。 什么是预测?预测就是要对连续的、数值型的、有序的值进行建模。例如在 上面的例子中,我们收集到了很多历史数据,也就是包括了以往车型的发动机的 指标以及它们的二氧化碳的排放量,找到它们互相之间的关系,建立一个模型, 将新车的各项指标作为模型的参数的输入,就可以得到作为输出的这款汽车预估
我们可以收集以往车型的技术指标和二氧化碳的排放量,然后找到它们之间 的内在关系,构建出相应的模型,通过这个模型我们就可以来预测未来车型的二 氧化碳的排放量。我们抽取收集到的历史数据当中的几列来看一看,包括发动机 的大小、气缸数、百公里综合油耗和二氧化碳的排放量,我们会发现前三列与发 动机相关的技术指标与二氧化碳排放量之间存在着正相关的关系,所以我们认为 一辆汽车的二氧化碳的排放量和发动机的相关指数是存在着关联关系的。 所以我们面临的问题是什么?就是当一辆汽车被设计出来,但是还没有被制 造出来的时候,我们能不能在不经过实际的实车测试的情况下就能够预测出来, 这辆汽车未来可能的二氧化碳的排放量,这样我们就可以判断这个设计方案是否 能够符合国家的相应的排放标准。显然这不是一个很容易解决的问题,但是我们 刚才已经提到了一个方案,就是我们要去计算二氧化碳排放量和发动机的各种技 术指标,包括排量、类型、模式、气缸数、油耗等之间的关系,通过计算出来的 关系模型来预测未来车型的二氧化碳的排放量。 什么是预测?预测就是要对连续的、数值型的、有序的值进行建模。例如在 上面的例子中,我们收集到了很多历史数据,也就是包括了以往车型的发动机的 指标以及它们的二氧化碳的排放量,找到它们互相之间的关系,建立一个模型, 将新车的各项指标作为模型的参数的输入,就可以得到作为输出的这款汽车预估

的二氧化碳的排放量。 历史数据:以往车型的发动机 的排量、类型、模式、汽缸 油耗、CO2排放量等 模型 New Car Expected Co2 怎么来做预测呢?做预测通常要遵循下面的步骤:首先,我们要把收集到的 数据分为训练集和测试集两部分,其中训练集要占到整个数据集的80%左右,剩 下的是测试集。我们先用训练集来训练模型,得到了模型之后用测试集对它进行 评估。通过评估之后,这个模型就可以用来对未来的值进行预测。所以我们看到 在下面的数据集中,棕色的这一列表示我们要预测的二氧化碳的排放量,所以它 被称为目标列。所有跟目标列相关的其他列,包括发动机的汽缸数、发动机的大 小、百公里综合油耗等等都被称为特征列。所有的数据集分成80%的数据构成的 训练集以及剩下的20%的数据构成的测试集,或者叫评估集,评估之后就可以对 未来的值进行预测。 特征 目标 Cylinder Engine Cons C02 Size 3 3 112 1 4 1 … 125 训练集 1 2 2 … 101 3 3 108 3 4 1 … 105 2 2 102 测试/评估集 2 3 3 121 1 2 4 2 预测集 这是在Python上创建训练集和测试集的脚本。它取出整个数据集的总长度
的二氧化碳的排放量。 怎么来做预测呢?做预测通常要遵循下面的步骤:首先,我们要把收集到的 数据分为训练集和测试集两部分,其中训练集要占到整个数据集的 80%左右,剩 下的是测试集。我们先用训练集来训练模型,得到了模型之后用测试集对它进行 评估。通过评估之后,这个模型就可以用来对未来的值进行预测。所以我们看到 在下面的数据集中,棕色的这一列表示我们要预测的二氧化碳的排放量,所以它 被称为目标列。所有跟目标列相关的其他列,包括发动机的汽缸数、发动机的大 小、百公里综合油耗等等都被称为特征列。所有的数据集分成 80%的数据构成的 训练集以及剩下的 20%的数据构成的测试集,或者叫评估集,评估之后就可以对 未来的值进行预测。 这是在P瀌瀇濻瀂瀁上创建训练集和测试集的脚本。它取出整个数据集的总长度

创建一个小于这个总长度0.8的随机数,实际上这个值会非常接近0.8,然后拿 这个值作为百分比,获取整个汽车数据中80%的数据作为训练集,剩下的数据就 是测试集。在真正进行预测的时候,我们可以用到的算法有很多选择,首先是回 归分析,然后是K近邻方法、神经网络和支持向量机。 Creating train and test dataset msk np.random.rand(len(df))<0.8 train cdf[msk] test cdf[-msk] 我们将重点关注回归分析。在回归分析中,根据自变量的数量多少,我们又 可以分为简单回归和多元回归。根据构建出来的模型的类型,又可以分为线性回 归和非线性回归。 所谓简单回归,就是指我们要预测的值只和单个的自变量相关。例如,我们 认为二氧化碳的排放量和汽车的大小相关,并且只和汽车大小相关。这时,我们 就可以使用到简单回归。这时预测的因变量就是二氧化碳的排放量,而自变量就 是发动机的大小。如果我们认为二氧化碳的排放量和发动机的大小之外的其他变 量也存在着关联,那么就要使用到多元回归,此时因变量仍然是二氧化碳的排放 量,但自变量就包含了发动机的尺寸、发动机的缸数等等其他的多个因素。所以 我们看什么是回归分析?回归分析就是要找到一个变量与其他变量之间的关系, 也就是说我们认为一个变量是依赖于其他变量的,如果这个被依赖的变量也就是 自变量只有一个,就是我们所谓的简单回归分析,如果自变量有多个,那就是多 元回归分析。回归分析的应用场景很多,包括市场销量的预测,心理学上的满意 度分析等等。 简单线性模型是最简单的一类回归分析模型,它的目标值预期是输入变量的
创建一个小于这个总长度 0.8 的随机数,实际上这个值会非常接近 0.8,然后拿 这个值作为百分比,获取整个汽车数据中 80%的数据作为训练集,剩下的数据就 是测试集。在真正进行预测的时候,我们可以用到的算法有很多选择,首先是回 归分析,然后是 K 近邻方法、神经网络和支持向量机。 我们将重点关注回归分析。在回归分析中,根据自变量的数量多少,我们又 可以分为简单回归和多元回归。根据构建出来的模型的类型,又可以分为线性回 归和非线性回归。 所谓简单回归,就是指我们要预测的值只和单个的自变量相关。例如,我们 认为二氧化碳的排放量和汽车的大小相关,并且只和汽车大小相关。这时,我们 就可以使用到简单回归。这时预测的因变量就是二氧化碳的排放量,而自变量就 是发动机的大小。如果我们认为二氧化碳的排放量和发动机的大小之外的其他变 量也存在着关联,那么就要使用到多元回归,此时因变量仍然是二氧化碳的排放 量,但自变量就包含了发动机的尺寸、发动机的缸数等等其他的多个因素。所以 我们看什么是回归分析?回归分析就是要找到一个变量与其他变量之间的关系, 也就是说我们认为一个变量是依赖于其他变量的,如果这个被依赖的变量也就是 自变量只有一个,就是我们所谓的简单回归分析,如果自变量有多个,那就是多 元回归分析。回归分析的应用场景很多,包括市场销量的预测,心理学上的满意 度分析等等。 简单线性模型是最简单的一类回归分析模型,它的目标值预期是输入变量的
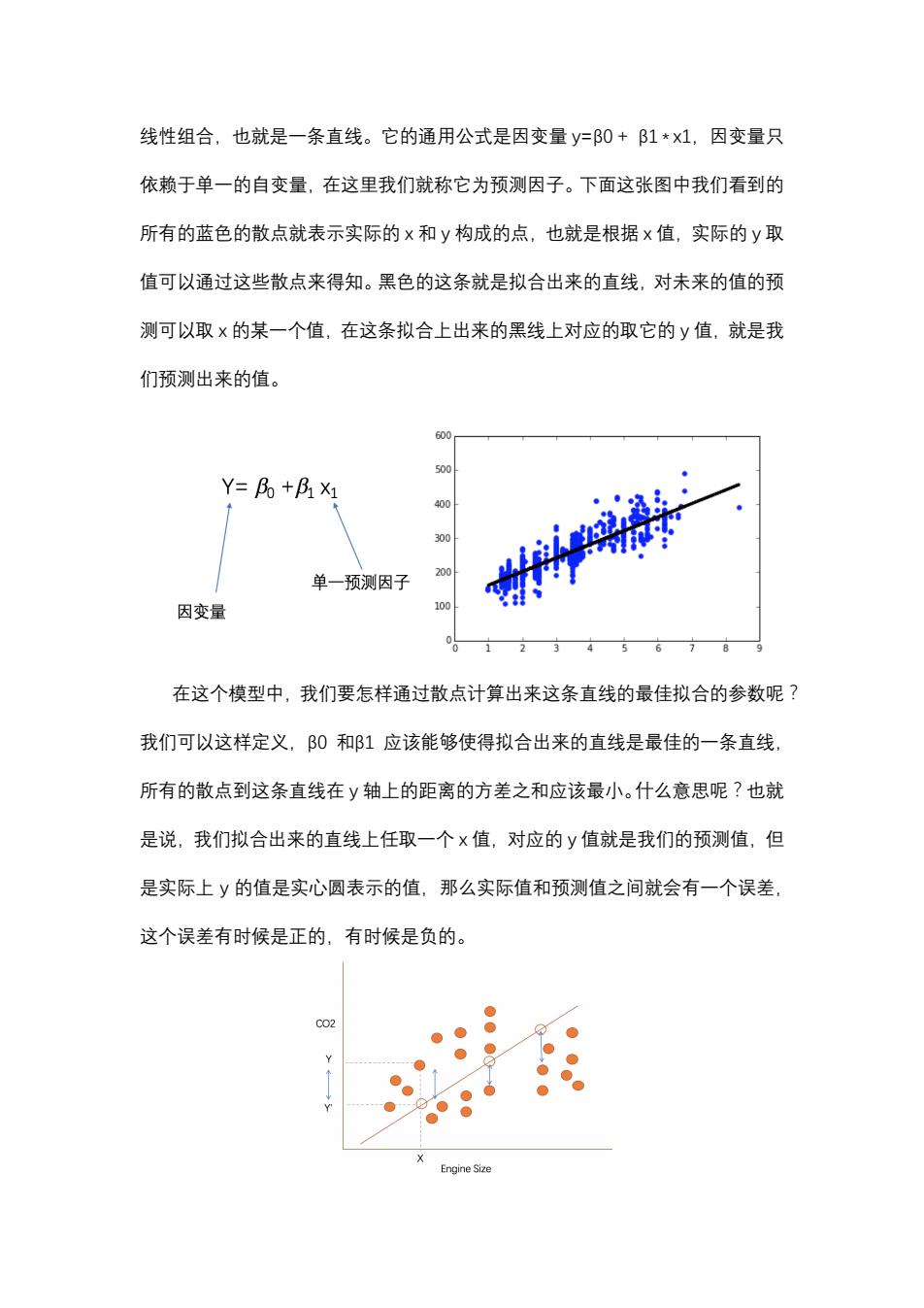
线性组合,也就是一条直线。它的通用公式是因变量y=β0+B1*x1,因变量只 依赖于单一的自变量,在这里我们就称它为预测因子。下面这张图中我们看到的 所有的蓝色的散点就表示实际的x和y构成的点,也就是根据x值,实际的y取 值可以通过这些散点来得知。黑色的这条就是拟合出来的直线,对未来的值的预 测可以取x的某一个值,在这条拟合上出来的黑线上对应的取它的y值,就是我 们预测出来的值。 500 Y=Bo+B1 X1 400 300 单一预测因子 200 因变量 100 在这个模型中,我们要怎样通过散点计算出来这条直线的最佳拟合的参数呢? 我们可以这样定义,B0和β1应该能够使得拟合出来的直线是最佳的一条直线, 所有的散点到这条直线在y轴上的距离的方差之和应该最小。什么意思呢?也就 是说,我们拟合出来的直线上任取一个x值,对应的y值就是我们的预测值,但 是实际上y的值是实心圆表示的值,那么实际值和预测值之间就会有一个误差, 这个误差有时候是正的,有时候是负的。 C02 Engine Size
线性组合,也就是一条直线。它的通用公式是因变量 瀌=β0 + β1 * 瀋1,因变量只 依赖于单一的自变量,在这里我们就称它为预测因子。下面这张图中我们看到的 所有的蓝色的散点就表示实际的 瀋 和 瀌 构成的点,也就是根据 瀋 值,实际的 瀌 取 值可以通过这些散点来得知。黑色的这条就是拟合出来的直线,对未来的值的预 测可以取 瀋 的某一个值,在这条拟合上出来的黑线上对应的取它的 瀌 值,就是我 们预测出来的值。 在这个模型中,我们要怎样通过散点计算出来这条直线的最佳拟合的参数呢? 我们可以这样定义,β0 和β1 应该能够使得拟合出来的直线是最佳的一条直线, 所有的散点到这条直线在 瀌 轴上的距离的方差之和应该最小。什么意思呢?也就 是说,我们拟合出来的直线上任取一个 瀋 值,对应的 瀌 值就是我们的预测值,但 是实际上 瀌 的值是实心圆表示的值,那么实际值和预测值之间就会有一个误差, 这个误差有时候是正的,有时候是负的

为了表示这条直线能够最好地拟合所有的点,我们把这些正误差和负误差通 通平方一下,然后累加,方差和最小的那条直线,就是拟合最好的直线,所以实 际上在这里我们用到了最小二乘法。最小二乘法的数学描述就是把所有的β值表 示成一个向量,如果每一个实际的y的取值与通过x的取值与β向量的乘积产生 的预测值之间的方差累加起来最小,那么这就是我们要找得这条向量,所以我们 可以看到最佳拟合直线产生的残值残差平方和是最小的。 MIN) 怎样计算简单线性模型中的β向量呢?下面是最小二乘法给出的计算公式, 用每一个x的值与x的平均值的差和y的值与y的平均值的差的积累加起来,除 以×与x的平均值的方差的累加和就得到了B1。B0是基于B1计算的,它等于y 的平均值减去β1乘以×的平均值。它的数学原理在这里我们就不用去深究了。 感兴趣的同学可以自己去查看它的证明和推导过程。 B。=y-月x 为什么不用深究呢?因为Python已经帮我们把这些功能实现了。例如,下 面是一个通过最小二乘法来计算刚才我们看到的β0和β1的脚本。首先,我们从 sklearn这个库里面导入线性模型,然后在线性模型这个对象上获取线性回归模 型对象。我们抽取训练集当中的两列:发动机的大小和二氧化碳的排放量,分别 放到train_x、train_y中,然后调用刚才的线性回归模型对象上的ft方法,传递 进去自变量数组和因变量数组,也就是train_x、train_y,那么它就会自动地帮我 们计算出来相应的β0和β1,也就是说它会自动地产生拟合出来的直线。我们最 后可以通过两个print的方法得到β1是38.68021623,而β0,也就是截距,是
为了表示这条直线能够最好地拟合所有的点,我们把这些正误差和负误差通 通平方一下,然后累加,方差和最小的那条直线,就是拟合最好的直线,所以实 际上在这里我们用到了最小二乘法。最小二乘法的数学描述就是把所有的β值表 示成一个向量,如果每一个实际的 瀌 的取值与通过 瀋 的取值与β向量的乘积产生 的预测值之间的方差累加起来最小,那么这就是我们要找得这条向量,所以我们 可以看到最佳拟合直线产生的残值残差平方和是最小的。 怎样计算简单线性模型中的β向量呢?下面是最小二乘法给出的计算公式, 用每一个 瀋 的值与 瀋 的平均值的差和 瀌 的值与 瀌 的平均值的差的积累加起来,除 以 瀋 与 瀋 的平均值的方差的累加和就得到了β1。β0 是基于β1 计算的,它等于 瀌 的平均值减去β1 乘以 瀋 的平均值。它的数学原理在这里我们就不用去深究了。 感兴趣的同学可以自己去查看它的证明和推导过程。 为什么不用深究呢?因为 P瀌瀇濻瀂瀁 已经帮我们把这些功能实现了。例如,下 面是一个通过最小二乘法来计算刚才我们看到的β0 和β1 的脚本。首先,我们从 瀆濾濿濸濴瀅瀁 这个库里面导入线性模型,然后在线性模型这个对象上获取线性回归模 型对象。我们抽取训练集当中的两列:发动机的大小和二氧化碳的排放量,分别 放到 瀇瀅濴濼瀁_瀋、瀇瀅濴濼瀁_瀌 中,然后调用刚才的线性回归模型对象上的 濹濼瀇 方法,传递 进去自变量数组和因变量数组,也就是 瀇瀅濴濼瀁_瀋、瀇瀅濴濼瀁_瀌,那么它就会自动地帮我 们计算出来相应的β0 和β1,也就是说它会自动地产生拟合出来的直线。我们最 后可以通过两个 瀃瀅濼瀁瀇 的方法得到β1 是 38.68021623,而β0,也就是截距,是

126.61208813,所以通过Python的线性回归对象调用其fit方法,就可以帮我们 自动去拟合出来两个数据集之间的线性关系。 from sklearn import linear model regr linear model.LinearRegression() train_x=np.asanyarray(train[['ENGINESIZE']] train y=np.asanyarray(train[['CO2EMISSIONS']] regr.fit (train x,train y) The coefficients print 'Coefficients:'regr.coef print 'Intercept:',regr.intercept Coefficients:[38.68021623]] Intercept:[126,61208813] 如果自变量有多个,那就是一个多元线性回归,也就是y=B0+B1*x1+B 2*x2++Bn*n,其中y仍然是因变量,x1到n是自变量,B1到Bn是对 应的自变量的系数,B0是截距。每一个跟自变量相关的系数都表示了这个自变 量与因变量之间的关系,即如果要是大于零,说明它们是正相关的,如果要是 小于零,说明它们是负相关的,如果等于0,就表示它们不相关。怎么才能找到 合适的值呢?可以通过最小二乘法的扩展来计算出来从B0到β的值,甚至有许 多不是线性函数的非线性函数也可以转换成上面的形式来计算,具体的数学推导 我们这里就不在深入讨论了,因为Python同样可以帮我们做好。我们可以举个 例子,假设我们认为汽车的功率、重量、发动机尺寸和在高速公路上的百公里综 合油耗与汽车的售价之间存在着关联关系,这是一个典型的多元线性回归模型。 z df[['horsepower','curb-weight','engine-size','highway-mpg'] Fit the linear model using the four above-mentioned variables. multi_fit 1m.fit(2,df['price']) multi fit LinearRegression(copy_X=True,fit_intercept=True,n_jobs=1,normalize=False) 现在的因变量是汽车的价格,而它的自变量包含了四个变量,我们可以通过 线性回归的函数给出相应的结果,我们将数据集这四列装载到一个叫z的数据集
126.61208813,所以通过 P瀌瀇濻瀂瀁 的线性回归对象调用其 濹濼瀇 方法,就可以帮我们 自动去拟合出来两个数据集之间的线性关系。 如果自变量有多个,那就是一个多元线性回归,也就是 瀌=β0 + β1 * 瀋1 + β 2 * 瀋2 + … + β瀁 * 瀋瀁,其中 瀌 仍然是因变量,瀋1 到 瀋瀁 是自变量,β1 到β瀁 是对 应的自变量的系数,β0 是截距。每一个跟自变量相关的系数都表示了这个自变 量与因变量之间的关系,即β濼 如果要是大于零,说明它们是正相关的,如果要是 小于零,说明它们是负相关的,如果等于 0,就表示它们不相关。怎么才能找到 合适的值呢?可以通过最小二乘法的扩展来计算出来从β0 到β瀁 的值,甚至有许 多不是线性函数的非线性函数也可以转换成上面的形式来计算,具体的数学推导 我们这里就不在深入讨论了,因为 P瀌瀇濻瀂瀁 同样可以帮我们做好。我们可以举个 例子,假设我们认为汽车的功率、重量、发动机尺寸和在高速公路上的百公里综 合油耗与汽车的售价之间存在着关联关系,这是一个典型的多元线性回归模型。 现在的因变量是汽车的价格,而它的自变量包含了四个变量,我们可以通过 线性回归的函数给出相应的结果,我们将数据集这四列装载到一个叫 瀍 的数据集

中,然后通过调用拟合函数找到自变量z数据集与因变量price数据集之间的关 系,我们就可以得到它算出来的截距以及在四个变量上的β值。最后我们可以得 到pice和这四个参数之间的线性模型,这就是我们看到的最终的结果。 1m.intercept_ -15678,742628061467 lm.coef_ array([52.65851272, 4.69878948,81.95906216,33.58258185]) Price =-15678.74 +(52.66)horsepower +(4.70)*curb-weight +(81.96)* engine-size +(33.58)*highway-mpg 如果回归的时候我们发现对应的模型不是线性模型怎么办?例如,像多项式 函数描述的非线性的模型该如何处理?假设y=β0+B1*×+B2*xA2+β3* x八3,这时我们看到的,出现了高次(X平方和×立方),说明这个模型就不是线性 模型。这时在数学上的处理是引入新的变量,将x2和3引入,分别表示x平方 和x立方,把整个上面的公式就转换成了一个新的多元线性回归模型y=β0+ B1*X+β2*x2+B3*x3,通过这种方式来解决。 三、模型评估和可视化 我们是通过可视化来评估模型的。我们为什么要评估模型,原因是因为我们 想知道开发出来的模型能不能用做预测模型来预测未来的值。在评估的时候,我
中,然后通过调用拟合函数找到自变量 瀍 数据集与因变量 瀃瀅濼濶濸 数据集之间的关 系,我们就可以得到它算出来的截距以及在四个变量上的β值。最后我们可以得 到 瀃瀅濼濶濸 和这四个参数之间的线性模型,这就是我们看到的最终的结果。 P瀅濼濶濸 = -15678.74 + (52.66 ) * 濻瀂瀅瀆濸瀃瀂瀊濸瀅 + (4.70) * 濶瀈瀅濵-瀊濸濼濺濻瀇 + (81.96) * 濸瀁濺濼瀁濸-瀆濼瀍濸 + (33.58) * 濻濼濺濻瀊濴瀌-瀀瀃濺 如果回归的时候我们发现对应的模型不是线性模型怎么办?例如,像多项式 函数描述的非线性的模型该如何处理?假设 瀌 = β0 + β1 * 瀋 + β2 * 瀋^2 + β3 * 瀋^3,这时我们看到的,出现了高次(瀋 平方和 瀋 立方),说明这个模型就不是线性 模型。这时在数学上的处理是引入新的变量,将 瀋2 和 瀋3 引入,分别表示 瀋 平方 和 瀋 立方,把整个上面的公式就转换成了一个新的多元线性回归模型 瀌 = β0 + β1 * 瀋 + β2 * 瀋2 + β3 * 瀋3,通过这种方式来解决。 三、模型评估和可视化 我们是通过可视化来评估模型的。我们为什么要评估模型,原因是因为我们 想知道开发出来的模型能不能用做预测模型来预测未来的值。在评估的时候,我
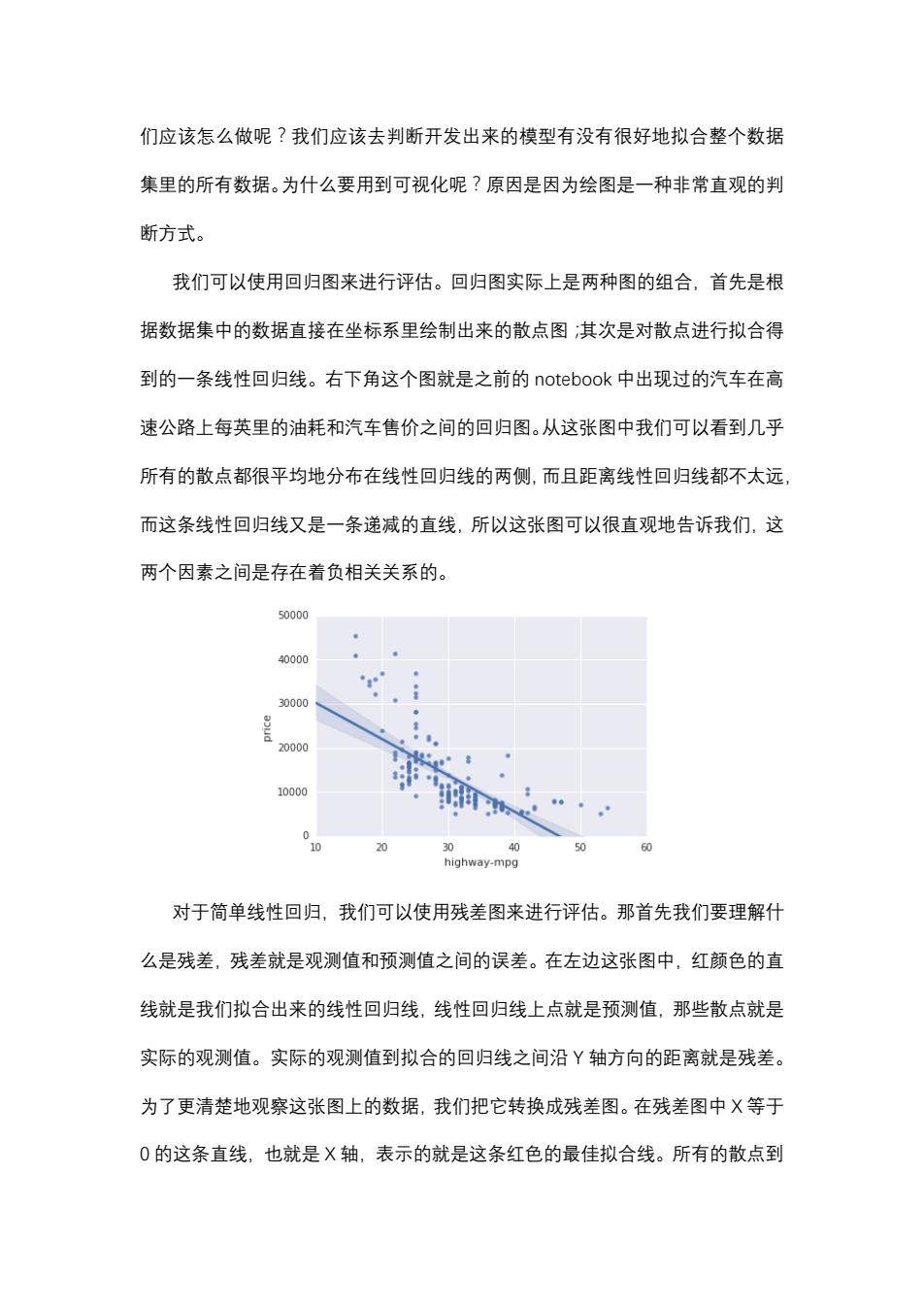
们应该怎么做呢?我们应该去判断开发出来的模型有没有很好地拟合整个数据 集里的所有数据。为什么要用到可视化呢?原因是因为绘图是一种非常直观的判 断方式。 我们可以使用回归图来进行评估。回归图实际上是两种图的组合,首先是根 据数据集中的数据直接在坐标系里绘制出来的散点图:其次是对散点进行拟合得 到的一条线性回归线。右下角这个图就是之前的notebook中出现过的汽车在高 速公路上每英里的油耗和汽车售价之间的回归图。从这张图中我们可以看到几乎 所有的散点都很平均地分布在线性回归线的两侧,而且距离线性回归线都不太远 而这条线性回归线又是一条递减的直线,所以这张图可以很直观地告诉我们,这 两个因素之间是存在着负相关关系的。 50000 40000 30000 20000 10000 0 20 0 40 50 60 highway-mpg 对于简单线性回归,我们可以使用残差图来进行评估。那首先我们要理解什 么是残差,残差就是观测值和预测值之间的误差。在左边这张图中,红颜色的直 线就是我们拟合出来的线性回归线,线性回归线上点就是预测值,那些散点就是 实际的观测值。实际的观测值到拟合的回归线之间沿Y轴方向的距离就是残差。 为了更清楚地观察这张图上的数据,我们把它转换成残差图。在残差图中X等于 0的这条直线,也就是X轴,表示的就是这条红色的最佳拟合线。所有的散点到
们应该怎么做呢?我们应该去判断开发出来的模型有没有很好地拟合整个数据 集里的所有数据。为什么要用到可视化呢?原因是因为绘图是一种非常直观的判 断方式。 我们可以使用回归图来进行评估。回归图实际上是两种图的组合,首先是根 据数据集中的数据直接在坐标系里绘制出来的散点图;其次是对散点进行拟合得 到的一条线性回归线。右下角这个图就是之前的 瀁瀂瀇濸濵瀂瀂濾 中出现过的汽车在高 速公路上每英里的油耗和汽车售价之间的回归图。从这张图中我们可以看到几乎 所有的散点都很平均地分布在线性回归线的两侧,而且距离线性回归线都不太远, 而这条线性回归线又是一条递减的直线,所以这张图可以很直观地告诉我们,这 两个因素之间是存在着负相关关系的。 对于简单线性回归,我们可以使用残差图来进行评估。那首先我们要理解什 么是残差,残差就是观测值和预测值之间的误差。在左边这张图中,红颜色的直 线就是我们拟合出来的线性回归线,线性回归线上点就是预测值,那些散点就是 实际的观测值。实际的观测值到拟合的回归线之间沿 Y 轴方向的距离就是残差。 为了更清楚地观察这张图上的数据,我们把它转换成残差图。在残差图中 X 等于 0 的这条直线,也就是 X 轴,表示的就是这条红色的最佳拟合线。所有的散点到