
《高等数学(二)》教学大纲6 (2010版) 课程编码:090003 课程名称:高等数学 学时/学分:66/4 先修课程:《初等数学》、《立体几何》、《平面解析几何》、《高等数学(一)》 适用专业:物理学等专业 开课教研室:大学数学教研室 执笔:顾敏娜 审定:王仁举赵国喜
《高等数学(二)》教学大纲 6 (2010 版) 课程编码:090003 课程名称:高等数学 学时/学分:66/4 先修课程:《初等数学》、《立体几何》、《平面解析几何》、《高等数学(一)》 适用专业:物理学等专业 开课教研室:大学数学教研室 执笔:顾敏娜 审定:王仁举 赵国喜

《高等数学(二)》教学大纲6 (2010版) 课程编码:090003 课程名称:高等数学 学时/学分:66/4 先修课程:《初等数学、《立体几何》、《平面解析几何》、《高等数学(一)》 适用专业:物理学等专业 开课教研室:大学数学教研室 执笔: 审定
《高等数学(二)》教学大纲 6 (2010 版) 课程编码:090003 课程名称:高等数学 学时/学分:66/4 先修课程:《初等数学》、《立体几何》、《平面解析几何》、《高等数学(一)》 适用专业:物理学等专业 开课教研室:大学数学教研室 执笔: 审定:

一、课程性质与任务 《高等数学(二)》是物理学等专业学生必修的重要基础理论课,它是为培养我国社会主义 现代化建设所需要的高质量专门人才服务。 通过本课程的学习,要使学生获得:1、微分方程:2、向量代数与空间解析几何:3、多元 函数微积分学:4、无穷级数(包括傅立叶级数)等方面的基本概念、基本理论和基本运算技能, 为学习后继课程和进一步获取数学知识莫定必要的数学基础。 在传授知识的同时,要通过各个教学环节逐步培养学生具有抽象思维能力、逻辑推理能力、 空间想象能力、运算能力和自学能力,还要特别注意培养学生具有综合运用所学知识去分析问题 和解决问题的能力。 二、课程教学基本要求 《高等数学(二)》课程的安排在一年级第二个学期授课,共66个学时,设置4个学分。 说明:教学要求较高的内容用“理解”、“掌握”、“熟悉”等词表述,要求较低的内容用“了 解”、“会”等词表述。 一、常微分方程 1.了解微分方程、解、阶、通解、初始条件和特解等概念: 2.掌握变量可分离的方程及一阶线性方程的解法。会解齐次方程和伯努利(Bernoulli) 方程,了解用变量代换求解方程的思想: 3.会解全微分方程,能观察出最简单的积分因子: 4.会用降阶法解方程:ym=f(x),y"=f(x,y)和y"=fy,y'): 5.了解一阶微分方程解的存在性与唯一性定理及求近似解的步骤。了解奇解的概念: 6。理解线性微分方程解的结构,了解常数变易法: 7.掌握常系数齐次线性方程的解法,会求自由项形如 Pn(x)er和e[P.(x)cos Bx+P,(x)sin Bx]的常系数非齐次线性方程的特解: 8.会用微分方程解一些简单的几何问题和物理问题。 二、向量代数与空间解析几何 1.会计算二阶、三阶行列式: 2.理解空间直角坐标系: 3.理解向量的概念及其表示,掌握向量的运算(线性运算、数量积、向量积),掌握两个向 量垂直、平行的条件: 4.掌握单位向量、方向余弦、向量的坐标表达式以及用坐标表达式进行向量运算的方法: 5.掌握平面的方程和直线的方程及其求法,会利用平面、直线的相互关系解决有关问题: 6。理解曲面方程的概念,了解常用二次曲面的方程及其图形,了解以坐标轴为旋转轴的旋 转曲面及母线平行于坐标轴的柱面方程: 7.了解空间曲线的参数方程和一般方程:
一、课程性质与任务 《高等数学(二)》是物理学等专业学生必修的重要基础理论课,它是为培养我国社会主义 现代化建设所需要的高质量专门人才服务。 通过本课程的学习,要使学生获得:1、微分方程;2、向量代数与空间解析几何;3、多元 函数微积分学;4、无穷级数(包括傅立叶级数)等方面的基本概念、基本理论和基本运算技能, 为学习后继课程和进一步获取数学知识奠定必要的数学基础。 在传授知识的同时,要通过各个教学环节逐步培养学生具有抽象思维能力、逻辑推理能力、 空间想象能力、运算能力和自学能力,还要特别注意培养学生具有综合运用所学知识去分析问题 和解决问题的能力。 二、课程教学基本要求 《高等数学(二)》课程的安排在一年级第二个学期授课,共 66 个学时,设置 4 个学分。 说明:教学要求较高的内容用“理解”、“掌握”、“熟悉”等词表述,要求较低的内容用“了 解”、“会”等词表述。 一、常微分方程 1. 了解微分方程、解、阶、通解、初始条件和特解等概念; 2. 掌握变量可分离的方程及一阶线性方程的解法。会解齐次方程和伯努利(Bernoulli) 方程,了解用变量代换求解方程的思想; 3. 会解全微分方程,能观察出最简单的积分因子; 4. 会用降阶法解方程: ( ) ( ) n y f x , y f (x , y ) 和 y f ( y , y ) ; 5. 了解一阶微分方程解的存在性与唯一性定理及求近似解的步骤。了解奇解的概念; 6. 理解线性微分方程解的结构,了解常数变易法; 7. 掌握常系数齐次线性方程的解法,会求自由项形如 ( ) x Pn x e 和 [ ( ) cos ( )sin ] x n l e P x x P x x 的常系数非齐次线性方程的特解; 8. 会用微分方程解一些简单的几何问题和物理问题。 二、向量代数与空间解析几何 1. 会计算二阶、三阶行列式; 2. 理解空间直角坐标系; 3. 理解向量的概念及其表示,掌握向量的运算(线性运算、数量积、向量积),掌握两个向 量垂直、平行的条件; 4. 掌握单位向量、方向余弦、向量的坐标表达式以及用坐标表达式进行向量运算的方法; 5. 掌握平面的方程和直线的方程及其求法,会利用平面、直线的相互关系解决有关问题; 6. 理解曲面方程的概念,了解常用二次曲面的方程及其图形,了解以坐标轴为旋转轴的旋 转曲面及母线平行于坐标轴的柱面方程; 7. 了解空间曲线的参数方程和一般方程;

三、多元函数微分学 1.理解多元函数的概念。 2.了解二元函数的极限与连续性的概念,以及有界闭区域上连续函数的性质: 3.理解偏导数和全微分的概念,了解全微分存在的必要条件和充分条件,了解一阶全微分 形式的不变性: 4.了解方向导数与梯度的概念及其计算方法: 5.掌握复合函数一阶偏导数的求法,会求复合函数的二阶偏导数: 6.会求隐函数(包括由两个方程组成的方程组确定的隐函数)的偏导数: 7.了解曲线的切线和法平面及曲面的切平面与法线,并会求它们的方程: 8.理解多元函数极值与条件极值的概念,会求多元函数的极值。了解求条件极值的拉格朗 日乘数法,会求解一些较简单的最大值和最小值的应用问题。 四、多元函数积分学 1.理解二重积分、三重积分的概念及性质: 2.掌捉二重积分的计算方法(直角坐标、极坐标),了解三重积分的计算方法(值角坐标、柱 面坐标、球面坐标)。 3.理解两类曲线积分的概念、性质及相互间关系,掌握两类曲线积分的计算方法: 4.掌握格林(Green)公式及平面曲线积分与路径无关的条件: 5.理解两类曲面积分的概念、性质及相互间的关系,会计算两类曲面积分: 五、无穷级数 1.理解无穷级数收敛、发散以及和函数的概念,熟悉无穷级数基本性质及收敛的必要条件: 2.掌握几何级数和p一级数的收敛性: 3。了解正项级数的比较审敛法和极限审敛法,掌握正项级数的比值审敛法 成绩考核形式:平时成绩(平时测验、作业、课堂提问、课堂讨论等)(30%)+期终成绩 (闭卷考试)(70%),成绩评定采用百分制,60分为及格。 三、教学内容 第七章 微分方程 1.教学基本要求 让学生了解微分方程和差分方程的基本概念,掌握一些一阶微分方程的解法,二阶常系数的 齐次线性微分方程和差分方程的解法等。 2.要求学生掌握的基本概念、理论、技能 了解微分方程与差分方程的基本概念:掌握一些基本的一阶微分方程的求解方法;掌握一阶 常系数齐次线性差分方程的求解方法,学握一阶常系数非齐次线性差分方程的求解方法:会使用 降阶法解决一些特殊的高阶方程:了解二阶线性微分方程和差分方程解的结构:会求解二阶常系
三、多元函数微分学 1. 理解多元函数的概念; 2. 了解二元函数的极限与连续性的概念,以及有界闭区域上连续函数的性质; 3. 理解偏导数和全微分的概念,了解全微分存在的必要条件和充分条件,了解一阶全微分 形式的不变性; 4. 了解方向导数与梯度的概念及其计算方法; 5. 掌握复合函数一阶偏导数的求法,会求复合函数的二阶偏导数; 6. 会求隐函数(包括由两个方程组成的方程组确定的隐函数)的偏导数; 7. 了解曲线的切线和法平面及曲面的切平面与法线,并会求它们的方程; 8. 理解多元函数极值与条件极值的概念,会求多元函数的极值。了解求条件极值的拉格朗 日乘数法,会求解一些较简单的最大值和最小值的应用问题。 四、多元函数积分学 1. 理解二重积分、三重积分的概念及性质; 2. 掌握二重积分的计算方法(直角坐标、极坐标),了解三重积分的计算方法(直角坐标、柱 面坐标、球面坐标)。 3. 理解两类曲线积分的概念、性质及相互间关系,掌握两类曲线积分的计算方法; 4. 掌握格林(Green)公式及平面曲线积分与路径无关的条件; 5. 理解两类曲面积分的概念、性质及相互间的关系,会计算两类曲面积分; 五、无穷级数 1. 理解无穷级数收敛、发散以及和函数的概念,熟悉无穷级数基本性质及收敛的必要条件; 2. 掌握几何级数和 p--级数的收敛性; 3. 了解正项级数的比较审敛法和极限审敛法,掌握正项级数的比值审敛法; 成绩考核形式:平时成绩(平时测验、作业、课堂提问、课堂讨论等)(30%)+期终成绩 (闭卷考试)(70%),成绩评定采用百分制,60 分为及格。 三、教学内容 第七章 微分方程 1.教学基本要求 让学生了解微分方程和差分方程的基本概念,掌握一些一阶微分方程的解法,二阶常系数的 齐次线性微分方程和差分方程的解法等。 2.要求学生掌握的基本概念、理论、技能 了解微分方程与差分方程的基本概念;掌握一些基本的一阶微分方程的求解方法;掌握一阶 常系数齐次线性差分方程的求解方法,掌握一阶常系数非齐次线性差分方程的求解方法;会使用 降阶法解决一些特殊的高阶方程;了解二阶线性微分方程和差分方程解的结构;会求解二阶常系

数的齐次线性微分方程和差分方程,会求解一些简单的二阶常系数的非齐次线性微分方程和差分 方程。 3.教学重点和难点 教学重点是一阶微分方程的求解方法,一阶常系数齐次线性差分方程的求解方法,二阶常系 数的齐次线性微分方程和差分方程的解法等。教学难点是方程的求解方法。 4.教学内容 第一节 微分方程的基本概念 第二节 可分离变量的微分方程 第三节 齐次方程 1.齐次方程 第四节 一阶线性微分方程 .线性方程 第五节 可降阶的高阶微分方程 1.y可=∫(x)型的微分方程 2.y”=f(x,y)型的微分方程 3.y-fy,y)型的微分方程 第六节高阶线性微分方程 1,二阶线性微分方程举例 2.常数变易法 第七节 常系数齐次线性微分方程 第八节 常系数非齐次线性微分方程 1.fx)=e“P(x)型 2.f(x)=e“[P"(x)COS@x+P2(x)sin @x]型 第八章空间解析几何与向量代数 1.教学基本要求 让学生了解空间曲线和曲面的一般方程,了解二次曲面的概念,掌握空间曲线的投影柱面及 投影 2.要求学生掌握的基本概念、理论、技能 掌握母线平行与坐标轴的柱面及平面曲线绕坐标轴旋转所得的旋转曲面方程:能识别常用的 二次曲面方程,能用截痕法研究二次曲面的性质,并画出图形:知道空间曲线的一般方程,熟练 掌握空间曲线关于坐标面的投影柱面及在坐标面的投影,能画出投影区域。 3.教学重点和难点 教学重点是二次曲面的方程,图形以及空间曲线关于坐标面的投影柱面及在坐标面的投影。 教学难点是利用截痕法研究二次曲面的性质
数的齐次线性微分方程和差分方程,会求解一些简单的二阶常系数的非齐次线性微分方程和差分 方程。 3.教学重点和难点 教学重点是一阶微分方程的求解方法,一阶常系数齐次线性差分方程的求解方法,二阶常系 数的齐次线性微分方程和差分方程的解法等。教学难点是方程的求解方法。 4.教学内容 第一节 微分方程的基本概念 第二节 可分离变量的微分方程 第三节 齐次方程 1.齐次方程 第四节 一阶线性微分方程 1. 线性方程 第五节 可降阶的高阶微分方程 1. ( ) n y f x 型的微分方程 2. y f (x, y) 型的微分方程 3. y f ( y, y)型的微分方程 第六节 高阶线性微分方程 1. 二阶线性微分方程举例 2. 常数变易法 第七节 常系数齐次线性微分方程 第八节 常系数非齐次线性微分方程 1. ( ) ( ) x m f x e P x 型 2. (1) (2) ( ) ( ) cos ( )sin x l n f x e P x x P x x 型 第八章 空间解析几何与向量代数 1.教学基本要求 让学生了解空间曲线和曲面的一般方程,了解二次曲面的概念,掌握空间曲线的投影柱面及 投影。 2.要求学生掌握的基本概念、理论、技能 掌握母线平行与坐标轴的柱面及平面曲线绕坐标轴旋转所得的旋转曲面方程;能识别常用的 二次曲面方程,能用截痕法研究二次曲面的性质,并画出图形;知道空间曲线的一般方程,熟练 掌握空间曲线关于坐标面的投影柱面及在坐标面的投影,能画出投影区域。 3.教学重点和难点 教学重点是二次曲面的方程,图形以及空间曲线关于坐标面的投影柱面及在坐标面的投影。 教学难点是利用截痕法研究二次曲面的性质

4.教学内容 第一书向量及其线性运算 1.向量概念 2.向量的线性运算 3.空间直角坐标系 4.利用坐标作向量的线性运算 5.向量的模方向角投影 第二节数量积向量积 1.两向量的数量积 2.两向量的向量积 第三节 曲面及其方程 1.曲面方程的概念 2.旋转曲面 3.柱面 4.二次曲面 第四节 空间曲线及其方程 1.空间曲线的一般方程 2.空间曲线的参数方程 3.空何曲线在坐标面上的投影 第五节 空间曲线及其方程 1.平面的点法式方程 2.平面的一般方程 3.两平面的夹角 第六节 空间直线及其方程 1.空间直线的一般方程 2.空间直线的对称式方程与参数方程 3.两直线的夹角 4.直线与平面的夹角 5.杂例 第九章 多元函数微分法及其应用 1.教学基本要求 让学生了解多元函数微分学的有关概念,了解多元函数极值、最值的判定,了解多元函数微 分学的经济应用。 2.要求学生掌握的基本概念、理论、技能
4.教学内容 第一节 向量及其线性运算 1. 向量概念 2. 向量的线性运算 3. 空间直角坐标系 4. 利用坐标作向量的线性运算 5. 向量的模 方向角 投影 第二节 数量积 向量积 1. 两向量的数量积 2. 两向量的向量积 第三节 曲面及其方程 1. 曲面方程的概念 2. 旋转曲面 3. 柱面 4. 二次曲面 第四节 空间曲线及其方程 1. 空间曲线的一般方程 2. 空间曲线的参数方程 3. 空间曲线在坐标面上的投影 第五节 空间曲线及其方程 1. 平面的点法式方程 2. 平面的一般方程 3. 两平面的夹角 第六节 空间直线及其方程 1. 空间直线的一般方程 2. 空间直线的对称式方程与参数方程 3. 两直线的夹角 4. 直线与平面的夹角 5. 杂例 第九章 多元函数微分法及其应用 1.教学基本要求 让学生了解多元函数微分学的有关概念,了解多元函数极值、最值的判定,了解多元函数微 分学的经济应用。 2.要求学生掌握的基本概念、理论、技能

了解多元函数的极限和多元函数的连续性:掌握多元函数的偏导数概念,了解其几何意义 学握全微分的概念,知道多元函数全微分、偏导数和连续的关系:掌据多元函数的偏导数、高阶 偏导数和全微分的计算:掌握多元复合函数微分法,会求复合函数的偏导数、二阶偏导数:掌握 由一个方程确定的隐函数的偏导数的求法:了解多元函数极值、最值的判定:了解多元函数微分 学的经济应用,会用拉格朗日乘数法求条件极值。 3.教学重点和难点 教学重点是多元函数的偏导数和全微分,多元函数极值及其在经济上的应用。教学难点是多 元复合函数的求偏导 4.教学内容 第一节 多元函数的基本概念 1.平面点集 2.二元函数概念 3.多元函数的极限 4.多元函数的连续性 第二节 偏导数 1.偏导数的定义及其计算法 2.高阶偏导数 第三节全微分 1全微分的定义 第四节 多元复合函数的求导法则 第五节 隐函数的求导公式 .一个方程的情形 2.方程组的情形 第六节多元函数微分学的几何应用 1.一元向量值函数及其导数 2.空间曲线的切线与法平面 3.曲面的切平面 第七节 方向导数与梯度 1.方向导数 2.梯度 第八节 多元函数的极值及其求法 1.多元函数的极值及最大值最小值 2.条件极值拉格朗日乘数法 第十章 重积分
了解多元函数的极限和多元函数的连续性;掌握多元函数的偏导数概念,了解其几何意义, 掌握全微分的概念,知道多元函数全微分、偏导数和连续的关系;掌握多元函数的偏导数、高阶 偏导数和全微分的计算;掌握多元复合函数微分法,会求复合函数的偏导数、二阶偏导数;掌握 由一个方程确定的隐函数的偏导数的求法;了解多元函数极值、最值的判定;了解多元函数微分 学的经济应用,会用拉格朗日乘数法求条件极值。 3.教学重点和难点 教学重点是多元函数的偏导数和全微分,多元函数极值及其在经济上的应用。教学难点是多 元复合函数的求偏导。 4.教学内容 第一节 多元函数的基本概念 1. 平面点集 2. 二元函数概念 3. 多元函数的极限 4. 多元函数的连续性 第二节 偏导数 1. 偏导数的定义及其计算法 2. 高阶偏导数 第三节 全微分 1. 全微分的定义 第四节 多元复合函数的求导法则 第五节 隐函数的求导公式 1. 一个方程的情形 2. 方程组的情形 第六节 多元函数微分学的几何应用 1. 一元向量值函数及其导数 2. 空间曲线的切线与法平面 3. 曲面的切平面 第七节 方向导数与梯度 1. 方向导数 2. 梯度 第八节 多元函数的极值及其求法 1. 多元函数的极值及最大值 最小值 2. 条件极值 拉格朗日乘数法 第十章 重积分

1.教学基本要求 让学生了解重积分的基木概念及性质,掌握重积分的计算方法。 2.要求学生掌握的基本概念、理论、技能 理解重积分的概念及几何含义:了解重积分的性质:掌握直角坐标系和极坐标系中二重积分 的计算方法。 3.教学重点和难点 教学重点是二重积分的基本概念及性质、二重积分的计算方法。教学难点是二重积分的计算 方法。 4.教学内容 第一节 二重积分的概念与性质 1.二重积分的概念 2.二重积分的性质 第二节二重积分的计算法 1利用直角坐标计算二重积分 2.利用极坐标计算二重积分 第三节 三重积分 1.三重积分的概念 2.三重积分的计算 第四节重积分的应用 1.曲面的面积 2.质心 3.转动惯量 4.引力 第十一章 曲线积分与曲面积分 1.教学基本要求 让学生了解曲线积分和曲面积分的基本概念,掌握计算曲线积分和曲面积分的计算方法, 理解格林公式且能应用公式 2.要求学生掌握的基本概念、理论、技能 理解的曲线积分和曲面积分概念及含义:掌握曲线积分和曲面积分的计算方法。 3.教学重点和难点 教学重点是两类曲线积分的计算方法:格林公式及其应用:两类曲面积分的计算方法:高 斯公式、斯托克斯公式:两类曲线积分与两类曲面积分的应用。教学难点是两类曲线积分的关系 及两类曲面积分的关系:对坐标的曲线积分与对坐标的曲面积分的计算:应用格林公式计算对坐 标的曲线积分
1.教学基本要求 让学生了解重积分的基本概念及性质,掌握重积分的计算方法。 2.要求学生掌握的基本概念、理论、技能 理解重积分的概念及几何含义;了解重积分的性质;掌握直角坐标系和极坐标系中二重积分 的计算方法。 3.教学重点和难点 教学重点是二重积分的基本概念及性质、二重积分的计算方法。教学难点是二重积分的计算 方法。 4.教学内容 第一节 二重积分的概念与性质 1. 二重积分的概念 2. 二重积分的性质 第二节 二重积分的计算法 1. 利用直角坐标计算二重积分 2. 利用极坐标计算二重积分 第三节 三重积分 1. 三重积分的概念 2. 三重积分的计算 第四节 重积分的应用 1. 曲面的面积 2. 质心 3. 转动惯量 4. 引力 第十一章 曲线积分与曲面积分 1.教学基本要求 让学生了解曲线积分和曲面积分的基本概念,掌握计算曲线积分和曲面积分的计算方法, 理解格林公式且能应用公式。 2.要求学生掌握的基本概念、理论、技能 理解的曲线积分和曲面积分概念及含义;掌握曲线积分和曲面积分的计算方法。 3.教学重点和难点 教学重点是两类曲线积分的计算方法;格林公式及其应用;两类曲面积分的计算方法;高 斯公式、斯托克斯公式;两类曲线积分与两类曲面积分的应用。教学难点是两类曲线积分的关系 及两类曲面积分的关系;对坐标的曲线积分与对坐标的曲面积分的计算;应用格林公式计算对坐 标的曲线积分

4.教学内容 第一节对弧长的曲线积分 1.对弧长的曲线积分的概念与性质 2.对弧长的曲线积分的计算法 第二节对坐标的曲线积分 1.对坐标的曲线积分的概念与性质 2.对坐标的曲线积分的计算法 3.。两类曲线积分之间的联系 第三节格林公式及其应用 1.格林公式 2.平面上曲线积分与路径无关的条件 3.二元函数的全微分求积 第四节对面积的曲面积分 1.对面积的曲面积分的概念与性质 2.对面积的曲面积分的计算法 第五节 对坐标的曲面积分 1.对坐标的曲面积分的概念与性质 2.对坐标的曲面积分的计算法 3.两类曲面积分之间的联系 第十二章 无穷级数 1.教学基本要求 让学生了解无穷级数收敛、发散的概念,了解幂级数的概念及性质,会求简单幂级数的和函 数等。 2.要求学生掌握的基本概念、理论、技能 理解无穷级数收敛、发散的概念:掌捏无穷级数的基本性质及收敛的必要条件:了解正项级 数的比较审敛法,掌握几何级数与级数的敛散性的概念及二者的关系:了解交错级数的莱布尼 兹定理,了解绝对收敛与条件收敛的概念及二者的联系;掌握简单幂级数收敛区间的求法,掌捏 幂级数在其收敛区间内的基本性质,会求简单幂级数的和函数:掌握e,sinx,ln(l+x),(1+xy的 麦克劳林展开式等。 3.教学重点和难点 教学重点是无穷级数的概念及性质,判断正项级数和交错级数的敛散性,幂级数的概念及性 质。教学难点是幂级数收敛区间的求法,求幂级数的和函数等。 4.教学内容 第一节常数项级数的概念和性质
4.教学内容 第一节 对弧长的曲线积分 1. 对弧长的曲线积分的概念与性质 2. 对弧长的曲线积分的计算法 第二节 对坐标的曲线积分 1. 对坐标的曲线积分的概念与性质 2. 对坐标的曲线积分的计算法 3. 两类曲线积分之间的联系 第三节 格林公式及其应用 1. 格林公式 2. 平面上曲线积分与路径无关的条件 3. 二元函数的全微分求积 第四节 对面积的曲面积分 1. 对面积的曲面积分的概念与性质 2. 对面积的曲面积分的计算法 第五节 对坐标的曲面积分 1. 对坐标的曲面积分的概念与性质 2. 对坐标的曲面积分的计算法 3. 两类曲面积分之间的联系 第十二章 无穷级数 1.教学基本要求 让学生了解无穷级数收敛、发散的概念,了解幂级数的概念及性质,会求简单幂级数的和函 数等。 2.要求学生掌握的基本概念、理论、技能 理解无穷级数收敛、发散的概念;掌握无穷级数的基本性质及收敛的必要条件;了解正项级 数的比较审敛法,掌握几何级数与 p 级数的敛散性的概念及二者的关系;了解交错级数的莱布尼 兹定理,了解绝对收敛与条件收敛的概念及二者的联系;掌握简单幂级数收敛区间的求法,掌握 幂级数在其收敛区间内的基本性质,会求简单幂级数的和函数;掌握 ,sin ,ln(1 ),(1 ) x e x x x 的 麦克劳林展开式等。 3.教学重点和难点 教学重点是无穷级数的概念及性质,判断正项级数和交错级数的敛散性,幂级数的概念及性 质。教学难点是幂级数收敛区间的求法,求幂级数的和函数等。 4.教学内容 第一节 常数项级数的概念和性质
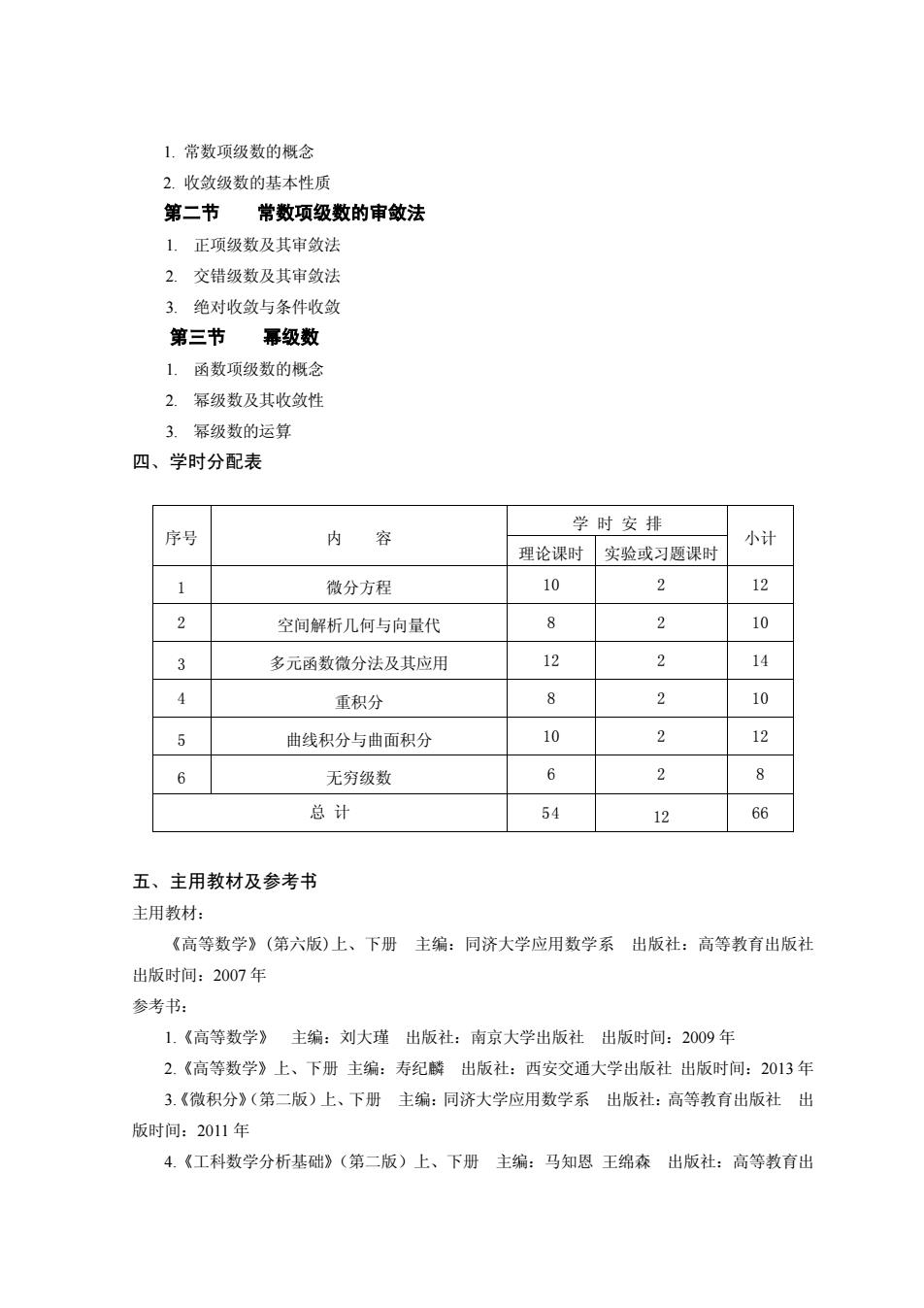
L.常数项级数的概念 2.收敛级数的基木性质 第二节常数项级数的审敛法 1正项级数及其审敛法 2.交错级数及其审敛法 3.绝对收敛与条件收敛 第三节幂级数 1.函数项级数的概念 2.幂级数及其收敛性 3.幂级数的运算 四、学时分配表 学时安排 序号 内容 理论课时实验或习题课时 小计 1 微分方程 10 12 2 空间解析几何与向量代 8 2 10 多元函数微分法及其应用 12 2 14 4 重积分 8 2 10 5 曲线积分与曲面积分 10 12 6 无穷级数 6 2 8 总计 54 12 66 五、主用教材及参考书 主用教材: 《高等数学》(第六版)上、下册主编:同济大学应用数学系出版社:高等教育出版社 出版时间:2007年 参考书: 1.《高等数学》主编:刘大瑾出版社:南京大学出版社出版时间:2009年 2.《高等数学》上、下册主编:寿纪麟出版社:西安交通大学出版社出版时间:2013年 3.《微积分》(第二版)上、下册主编:同济大学应用数学系出版社:高等教育出版社出 版时间:2011年 4.《工科数学分析基础》(第二版)上、下册主编:马知恩王绵森出版社:高等教育出
1. 常数项级数的概念 2. 收敛级数的基本性质 第二节 常数项级数的审敛法 1. 正项级数及其审敛法 2. 交错级数及其审敛法 3. 绝对收敛与条件收敛 第三节 幂级数 1. 函数项级数的概念 2. 幂级数及其收敛性 3. 幂级数的运算 四、学时分配表 学 时 安 排 序号 内 容 理论课时 实验或习题课时 小计 1 微分方程 10 2 12 2 空间解析几何与向量代 8 2 10 3 多元函数微分法及其应用 12 2 14 4 重积分 8 2 10 5 曲线积分与曲面积分 10 2 12 6 无穷级数 6 2 8 总 计 54 12 66 五、主用教材及参考书 主用教材: 《高等数学》(第六版)上、下册 主编:同济大学应用数学系 出版社:高等教育出版社 出版时间:2007 年 参考书: 1.《高等数学》 主编:刘大瑾 出版社:南京大学出版社 出版时间:2009 年 2.《高等数学》上、下册 主编:寿纪麟 出版社:西安交通大学出版社 出版时间:2013 年 3.《微积分》(第二版)上、下册 主编:同济大学应用数学系 出版社:高等教育出版社 出 版时间:2011 年 4.《工科数学分析基础》(第二版)上、下册 主编:马知恩 王绵森 出版社:高等教育出