
《概率论与数理统计》教学大纲2 (2010版) 课程编码:110834 课程名称:概率论与数理统计 学时/学分:54/3 先修课程:《初等数学》、《高等数学》、《线性代数》 适用专业:人力资源管理等专业 开课教研室:大学数学教研室 执笔:崔光云 审定:王仁举 赵国喜
《概率论与数理统计》教学大纲 2 (2010 版) 课程编码:110834 课程名称:概率论与数理统计 学时/学分:54/3 先修课程:《初等数学》、《高等数学》、《线性代数》 适用专业:人力资源管理等专业 开课教研室:大学数学教研室 执笔:崔光云 审定:王仁举 赵国喜

《概率论与数理统计》教学大纲2 (2010版) 课程编码:110834 课程名称:概率论与数理统计 学时/学分:54/3 先修课程:《初等数学》、《高等数学》、《线性代数 适用专业:人力资源管理等专业 开课教研室:大学数学教研室 执笔: 审定
《概率论与数理统计》教学大纲 2 (2010 版) 课程编码:110834 课程名称:概率论与数理统计 学时/学分:54/3 先修课程:《初等数学》、《高等数学》、《线性代数》 适用专业:人力资源管理等专业 开课教研室:大学数学教研室 执笔: 审定:

《概率论与数理统计》教学大纲 课程编码:110834 课程名称:概率论与数理统计 学时/学分:54/3 先修课程:《初等数学》、《高等数学》、《线性代数》 适用专业:人力资源管理等专业 开课教研室:大学数学教研室 一、课程性质与任务 1.课程性质:本课程是会计学专业的一门重要的专业基础课,是所有该专业学生的必修课 2.课程任务:本课程兼具基础性和应用性特征。教学目的包括两个方面:第一,通过本课 程的学习,使学生掌握概率论与数理统计的基本概念,了解它的基本理论和方法,从而使学生初 步掌握处理随机现象的基本思想和方法,培养学生运用概率统计方法分析和解决实际问邀的能 力。同时,为后续课程的学习打下坚实的基础:该课程能够使学生掌握概率与数理统计处理随机 现象中所蕴涵的带有普遍性的思想和方法,以使为学生分析和解决实际问题打下坚实的基础。 二、课程教学基本要求 1.随机事件及其概率 (①)理解随机事件的概念: (②)学握事件之间的关系与运算,掌握概率的基木性质和应用性质进行概率计算: (3)了解概率的定义: (4)理解条件概率和事件的独立性的概念: (⑤)掌握概率的加法公式、乘法公式、全概率公式、贝叶斯公式以及应用这些公式进行概率 计算。掌握应用事件独立性进行概率计算和二项概型及其计算。 2.随机变量及其数字特征 (1)理解随机变量的概念,理解随机变量分布函数的概念及性质,理解离散型和连续型随机 变量的概率分布及其性质,会应用概率分布计算有关事件的概率: (2)会求简单随机变量函数的概率分布 (③)了解二维随机变量概念及其它的联合分布函数概念和性质: (④)了解二维离散和连续随机变量定义及其它们的概率分布和性质,了解二维均匀分布和正 态分布: (⑤)会用它们计算有关事件的概率。会求解边缘分布: (⑥)掌握随机变量独立性的概念,掌握应用随机变量的独立性进行概率计算: (7)会求两个独立随机变量的简单函数的分布:
《概率论与数理统计》教学大纲 课程编码:110834 课程名称:概率论与数理统计 学时/学分:54/3 先修课程:《初等数学》、《高等数学》、《线性代数》 适用专业:人力资源管理等专业 开课教研室:大学数学教研室 一、课程性质与任务 1.课程性质:本课程是会计学专业的一门重要的专业基础课,是所有该专业学生的必修课。 2.课程任务:本课程兼具基础性和应用性特征。教学目的包括两个方面:第一,通过本课 程的学习,使学生掌握概率论与数理统计的基本概念,了解它的基本理论和方法,从而使学生初 步掌握处理随机现象的基本思想和方法,培养学生运用概率统计方法分析和解决实际问题的能 力。同时,为后续课程的学习打下坚实的基础;该课程能够使学生掌握概率与数理统计处理随机 现象中所蕴涵的带有普遍性的思想和方法,以便为学生分析和解决实际问题打下坚实的基础。 二、课程教学基本要求 1.随机事件及其概率 (1)理解随机事件的概念; (2)掌握事件之间的关系与运算, 掌握概率的基本性质和应用性质进行概率计算; (3)了解概率的定义; (4)理解条件概率和事件的独立性的概念; (5)掌握概率的加法公式、乘法公式、全概率公式、贝叶斯公式以及应用这些公式进行概率 计算。掌握应用事件独立性进行概率计算和二项概型及其计算。 2.随机变量及其数字特征 (1)理解随机变量的概念,理解随机变量分布函数的概念及性质, 理解离散型和连续型随机 变量的概率分布及其性质,会应用概率分布计算有关事件的概率; (2)会求简单随机变量函数的概率分布; (3)了解二维随机变量概念及其它的联合分布函数概念和性质; (4)了解二维离散和连续随机变量定义及其它们的概率分布和性质,了解二维均匀分布和正 态分布; (5)会用它们计算有关事件的概率。会求解边缘分布; (6)掌握随机变量独立性的概念,掌握应用随机变量的独立性进行概率计算; (7)会求两个独立随机变量的简单函数的分布;

(⑧)理解数学期望和方差的概念: (9)掌握数学期望和方差的性质与计算 (10)会计算随机变量函数的数学期望: (11)了解矩、协方差和相关系数的概念和性质,并会计算。 3.几种重要的分布 (1)掌握二项分布、泊松分布、正态分布、均匀分布和指数分布: (2)掌握二项分布、泊松分布和正态分布、均匀分布和指数分布的数学期望和方差: (3)能够准确计算二项分布、泊松分布和正态分布、均匀分布和指数分布数学期望和方差。 4.中心极限定理与参数估计 (1)了解切比雪夫不等式、大数定律和中心极限定理: (2)理解总体、样本和统计量的概念: (③)掌握样本均值、样本方差及样本矩的计算: (④)了解卡方分布、t~分布和F分布的定义及性质,了解分位数的概念并会查表计算: (⑤)掌握在正态总体下样本均值、样本方差、t统计量的分布及性质。 5.参数假设检验与一元线性回归分析 (1)理解显著性检验的基本思想: (2)掌握假设检验的基本步骤,了解假设检验可能产生的两类错误: (③)掌握单个正态总体均值和方差的假设检验,了解两个正态总体的均值和方差的假设检验: (4)理解一元线性回归分析的基本思想和方法。 主要教学环节包括课堂讲授、案例分析、小组讨论等。其中以课堂讲授为主,研制电子教案 和多媒体幻灯片以及CI课件,在教学方法和手段上采用现代教育技术。 成绩考核形式:平时成绩(平时测验、作业、课堂提问、课堂讨论等)(30%)+期末成绩(闭 卷考试)(70%),成绩评定采用百分制,60分为及格。 三、课程教学内容 第一章随机事件及其概率 1.教学基本要求 (1)了解样本空间的概念,理解随机事件的概念,掌握事件间的关系及运算。 (2)理解概率、条件概率的概念,掌捏概率的基本性质,会计算古典型概率:掌捏概率的 加法、乘法公式以及全概率公式、贝叶斯公式。 (3)理事件独立的概念,掌握用事件的独立性计算概率;理解重复独立试验的概念,掌 握伯务利概型概率的计算。 2.要求学生掌握的基本概念、理论、原理 随机事件的概仑及运算。概率的统计定义、古典定义及公理化定义。概率的基本性质、加法
(8)理解数学期望和方差的概念; (9)掌握数学期望和方差的性质与计算; (10)会计算随机变量函数的数学期望; (11)了解矩、协方差和相关系数的概念和性质,并会计算。 3.几种重要的分布 (1)掌握二项分布、泊松分布、正态分布、均匀分布和指数分布; (2)掌握二项分布、泊松分布和正态分布、均匀分布和指数分布的数学期望和方差; (3)能够准确计算二项分布、泊松分布和正态分布、均匀分布和指数分布数学期望和方差。 4.中心极限定理与参数估计 (1)了解切比雪夫不等式、大数定律和中心极限定理; (2)理解总体、样本和统计量的概念; (3)掌握样本均值、样本方差及样本矩的计算; (4)了解卡方分布、t-分布和 F 分布的定义及性质,了解分位数的概念并会查表计算; (5)掌握在正态总体下样本均值、样本方差、t 统计量的分布及性质。 5.参数假设检验与一元线性回归分析 (1)理解显著性检验的基本思想; (2)掌握假设检验的基本步骤,了解假设检验可能产生的两类错误; (3)掌握单个正态总体均值和方差的假设检验,了解两个正态总体的均值和方差的假设检验; (4)理解一元线性回归分析的基本思想和方法。 主要教学环节包括课堂讲授、案例分析、小组讨论等。其中以课堂讲授为主,研制电子教案 和多媒体幻灯片以及 CAI 课件,在教学方法和手段上采用现代教育技术。 成绩考核形式:平时成绩(平时测验、作业、课堂提问、课堂讨论等)(30%)+期末成绩(闭 卷考试)(70%),成绩评定采用百分制,60 分为及格。 三、课程教学内容 第一章 随机事件及其概率 1.教学基本要求 (1)了解样本空间的概念,理解随机事件的概念,掌握事件间的关系及运算。 (2)理解概率、条件概率的概念,掌握概率的基本性质,会计算古典型概率;掌握概率的 加法、乘法公式以及全概率公式、贝叶斯公式。 (3)理解事件独立的概念,掌握用事件的独立性计算概率;理解重复独立试验的概念,掌 握伯努利概型概率的计算。 2.要求学生掌握的基本概念、理论、原理 随机事件的概念及运算。概率的统计定义、古典定义及公理化定义。概率的基本性质、加法

公式、条件概率与乘法公式、全概率公式、贝叶斯公式。事件的独立性,独立随机试验、伯努利 公式。 3.教学重点和难点 教学重点是随机事件;概率的基本性质及其应用:乘法定理、全概率公式与贝叶斯公式事件 的独立性。教学难点是概率的公理化定义、条件概率概念的建立、全概率公式与贝叶斯公式应用。 4.教学内容 第一节 随机事件的概率 第二节 加法公式 第三节 乘法公式 第四节 全概公式 第二章 随机变量及其数字特征 1.教学基本要求 (1)理解随机变量及其分布的概念。理解分布函数的概念。会求与随机变量有关的事件的 概率: (2)掌握概率分布、概率密度与分布函数之间的关系,会灵活运用它们的性质: (3)理解随机变量独立性的概念,掌握独立的充要条件及其性质: (4)会利用自变量的分布,求简单一元随机变量函数的分布,会求简单二元离散型随机变 最函数的分布,以及二元连续型随机变量和函数的分布: (5)理解数学期望、方差、协方差、相关系数和不相关的概念: (6)会计算数学期望、方差、协方差和相关系数。掌握常用分布的数学期望和方差 (7)会利用自变量的分布求随机变量函数的数学期望、方差。 2.要求学生掌握的基本概念、理论、原理 一元随机变量及其概率分布的概念。随机变量的分布函数及其性质。离散型随机变量的概率 分布、连续型随机变量的概率密度以及它们的性质。几种常见的离散型分布和连续型分布。二元 随机变量及其联合分布的概念。二元随机变量的分布函数及其性质。离散型随机变量的联合分布、 边缘分布及条件分布,连续型随机变量的联合密度、边缘密度及条件密度,以及它们的性质。随 机变量的相互独立性。随机变量的数学期望、方差、标准差及其性质。随机变量函数的数学期望。 两个随机变量的协方差、相关系数及其性质。 3.教学重点和难点 教学重点是随机变量、分布律、密度函数和分布函数的概念:数学期望、方差、相关系数与 协方差的计算公式及性质。教学难点是随机变量函数的概率分布,随机变量函数的数学期望的计 算,利用数学期望的性质计算数学期望,相关系数的含义。 4.教学内容
公式、条件概率与乘法公式、全概率公式、贝叶斯公式。事件的独立性,独立随机试验、伯努利 公式。 3.教学重点和难点 教学重点是随机事件;概率的基本性质及其应用;乘法定理、全概率公式与贝叶斯公式事件 的独立性。教学难点是概率的公理化定义、条件概率概念的建立、全概率公式与贝叶斯公式应用。 4.教学内容 第一节 随机事件的概率 第二节 加法公式 第三节 乘法公式 第四节 全概公式 第二章 随机变量及其数字特征 1.教学基本要求 (1)理解随机变量及其分布的概念。理解分布函数的概念。会求与随机变量有关的事件的 概率; (2)掌握概率分布、概率密度与分布函数之间的关系,会灵活运用它们的性质; (3)理解随机变量独立性的概念,掌握独立的充要条件及其性质; (4)会利用自变量的分布,求简单一元随机变量函数的分布,会求简单二元离散型随机变 量函数的分布,以及二元连续型随机变量和函数的分布; (5)理解数学期望、方差、协方差、相关系数和不相关的概念; (6)会计算数学期望、方差、协方差和相关系数。掌握常用分布的数学期望和方差; (7)会利用自变量的分布求随机变量函数的数学期望、方差。 2.要求学生掌握的基本概念、理论、原理 一元随机变量及其概率分布的概念。随机变量的分布函数及其性质。离散型随机变量的概率 分布、连续型随机变量的概率密度以及它们的性质。几种常见的离散型分布和连续型分布。二元 随机变量及其联合分布的概念。二元随机变量的分布函数及其性质。离散型随机变量的联合分布、 边缘分布及条件分布,连续型随机变量的联合密度、边缘密度及条件密度,以及它们的性质。随 机变量的相互独立性。随机变量的数学期望、方差、标准差及其性质。随机变量函数的数学期望。 两个随机变量的协方差、相关系数及其性质。 3.教学重点和难点 教学重点是随机变量、分布律、密度函数和分布函数的概念;数学期望、方差、相关系数与 协方差的计算公式及性质。教学难点是随机变量函数的概率分布,随机变量函数的数学期望的计 算,利用数学期望的性质计算数学期望,相关系数的含义。 4.教学内容

第一节 离散型随机变量的概念 第二节 离散型随机变量的数字特征 第三节 连续型随机变量的概念 第四节 连续型随机变量的数字特征 第三章几种重要的概率分布 1.教学基本要求 (1)掌握0一1分布、二项分布、泊松分布和超几何分布。掌握二项分布的近似计算(用泊 松分布),掌握均匀分布、指数分布和正态分布: (2)理解二元随机变量、联合分布、边缘分布、条件分布的概念。会求离散型随机变量的 联合分布律。己知联合分布,会求边缘分布和条件分布。会利用二元分布求简单事件的概率: (3)掌握二元均匀分布,了解二元正态分布: 2.要求学生掌握的基本概念、理论、原理 0一1分布、二项分布、泊松分布和超几何分布,均匀分布、指数分布和正态分布,二元随 机变量、联合分布、边缘分布、条件分布的概念。 3.教学重点和难点 教学重点是二项分布、均匀分布、正态分布的概念和性质,教学难点是二项分布的推导及应 用,正态分布的图形及性质: 4.教学内容 第一节 二项分布 第二节 泊松分布 第三节 指数分布 第四节正态分布 第四章 中心极限定理与参数估计 1.教学基本要求 (1)了解依概率收敛的概念,了解大数定律的条件和结论以及它们的实际意义。会用切比雪 夫不等式估计有关事件的概率: (2)理解中心极限定理的条件和结论,并会用于计算有关随机事件的概率: (3)理解总体、样本、统计量等概念: (④了解卡方分布、t分布、F分布的定义和它们的图形,掌握分位点的概念并会查表 (⑤)掌握样本均值、样本方差的计算,掌握正态总体的某些常用统计量的分布: (6)理解参数的点估计的概念,掌挥矩估计法和最大似然估计法: (⑦)了解估计最的一致性,会验证估计量的无偏性及比较估计量的有效性: (8)了解区间估计的概念。掌握单个正态总体的均值和方差的区间估计,两个正态总体的均
第一节 离散型随机变量的概念 第二节 离散型随机变量的数字特征 第三节 连续型随机变量的概念 第四节 连续型随机变量的数字特征 第三章 几种重要的概率分布 1.教学基本要求 (1)掌握 0-1 分布、二项分布、泊松分布和超几何分布。掌握二项分布的近似计算(用泊 松分布),掌握均匀分布、指数分布和正态分布; (2)理解二元随机变量、联合分布、边缘分布、条件分布的概念。会求离散型随机变量的 联合分布律。已知联合分布,会求边缘分布和条件分布。会利用二元分布求简单事件的概率; (3)掌握二元均匀分布,了解二元正态分布; 2.要求学生掌握的基本概念、理论、原理 0-1 分布、二项分布、泊松分布和超几何分布, 均匀分布、指数分布和正态分布, 二元随 机变量、联合分布、边缘分布、条件分布的概念。 3.教学重点和难点 教学重点是二项分布、均匀分布、正态分布的概念和性质,教学难点是二项分布的推导及应 用,正态分布的图形及性质; 4.教学内容 第一节 二项分布 第二节 泊松分布 第三节 指数分布 第四节 正态分布 第四章 中心极限定理与参数估计 1.教学基本要求 (1)了解依概率收敛的概念,了解大数定律的条件和结论以及它们的实际意义。会用切比雪 夫不等式估计有关事件的概率; (2)理解中心极限定理的条件和结论,并会用于计算有关随机事件的概率; (3)理解总体、样本、统计量等概念; (4)了解卡方分布、t 分布、F 分布的定义和它们的图形,掌握分位点的概念并会查表; (5)掌握样本均值、样本方差的计算,掌握正态总体的某些常用统计量的分布; (6)理解参数的点估计的概念,掌握矩估计法和最大似然估计法; (7)了解估计量的一致性,会验证估计量的无偏性及比较估计量的有效性; (8)了解区间估计的概念。掌握单个正态总体的均值和方差的区间估计,两个正态总体的均

值差和方差比的区间估计。了解大样本下非正态总体参数的区间估计 2.要求学生掌握的基本概念、理论、原理 随机变量序列依概率收敛,切比雪夫不等式,切比雪夫大数定律、伯努利大数定律、辛钦大 数定律。林德伯格一列维定理(独立随机变量之和的极限分布)、棣莫弗一拉普拉斯定理(二项 分布以正态分布为极限分布)。总体、样本和统计量的概念。频率直方图,样本分布函数。样本 均值、样本方差、样本k阶原点矩、样本k阶中心矩。几个常用分布:卡方分布、t分布、F分 布及分位点。正态总体的某些常用统计量的分布。点估计的概念,矩估计法,最大似然估计法。 评价估计量优劣的标准:无偏性、有效性及一致性。区间估计的概念,单个正态总体的均值和方 差的置信区间,两个正态总体的均值差和方差比的置信区间。大样本下非正态总体参数的置信区 间,0一1总体中参数p的置信区间。 3.教学重点和难点 教学重点是用中心极限定理计算概率的近似值的方法,点估计的矩法、最大似然估计法:正 态总体参数的区间估计。教学难点是依概率收敛的概念,最大似然估计法,两个正态总体的参数 的区间估计的求法。 4.教学内容 第一节 中心极限定理 第二节 抽样分布 第三节 参数的点估计 第四节 参数的区间估计 第五章 参数假设检验与线性回归分析 1.教学基本要求 (1)理解显著性检验的基本思想: (2)掌握假设检验的基本步骤,了解假设检验可能产生的两类错误: (③)学握单个正态总体均值和方差的假设检验,了解两个正态总体的均值和方差的假设检验 (④)理解一元线性回归分析的基本思想和方法。 2.要求学生掌握的基本概念、理论、原理 显著性检验:单个正态总体均值和方差的假设检验:两个正态总体的均值和方差的假设检验: 一元线性回归分析的基本思想和方法。 3.教学重点和难点 教学重点是显著性检验的思想理解、单个正态总体均值和方差的假设检验、 元线性回归分 析的基本思想的理解:教学难点是两个正态总体的均值和方差的假设检验。 4.教学内容 第一节 参数假设检验的概念
值差和方差比的区间估计。了解大样本下非正态总体参数的区间估计。 2.要求学生掌握的基本概念、理论、原理 随机变量序列依概率收敛,切比雪夫不等式,切比雪夫大数定律、伯努利大数定律、辛钦大 数定律。林德伯格-列维定理(独立随机变量之和的极限分布)、棣莫弗-拉普拉斯定理(二项 分布以正态分布为极限分布)。总体、样本和统计量的概念。频率直方图,样本分布函数。样本 均值、样本方差、样本 k 阶原点矩、样本 k 阶中心矩。几个常用分布:卡方分布、t 分布、F 分 布及分位点。正态总体的某些常用统计量的分布。点估计的概念,矩估计法,最大似然估计法。 评价估计量优劣的标准:无偏性、有效性及一致性。区间估计的概念,单个正态总体的均值和方 差的置信区间,两个正态总体的均值差和方差比的置信区间。大样本下非正态总体参数的置信区 间,0-1 总体中参数 p 的置信区间。 3.教学重点和难点 教学重点是用中心极限定理计算概率的近似值的方法,点估计的矩法、最大似然估计法;正 态总体参数的区间估计。教学难点是依概率收敛的概念,最大似然估计法,两个正态总体的参数 的区间估计的求法。 4.教学内容 第一节 中心极限定理 第二节 抽样分布 第三节 参数的点估计 第四节 参数的区间估计 第五章 参数假设检验与线性回归分析 1.教学基本要求 (1)理解显著性检验的基本思想; (2)掌握假设检验的基本步骤,了解假设检验可能产生的两类错误; (3)掌握单个正态总体均值和方差的假设检验,了解两个正态总体的均值和方差的假设检验。 (4)理解一元线性回归分析的基本思想和方法。 2.要求学生掌握的基本概念、理论、原理 显著性检验;单个正态总体均值和方差的假设检验;两个正态总体的均值和方差的假设检验; 一元线性回归分析的基本思想和方法。 3.教学重点和难点 教学重点是显著性检验的思想理解、单个正态总体均值和方差的假设检验、一元线性回归分 析的基本思想的理解;教学难点是两个正态总体的均值和方差的假设检验。 4.教学内容 第一节 参数假设检验的概念
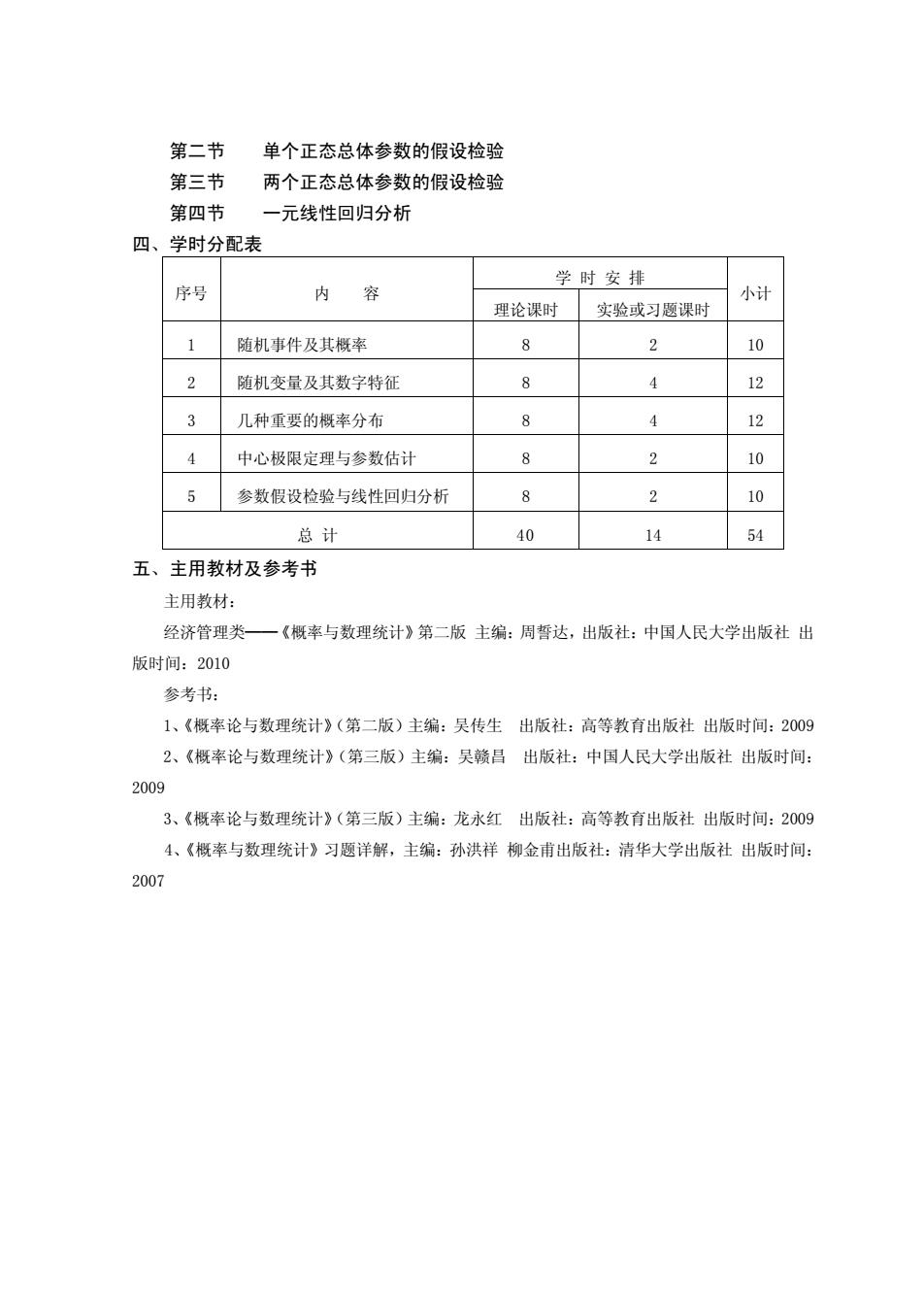
第二节 单个正态总体参数的假设检验 第三节 两个正态总体参数的假设检验 第四节 一元线性回归分析 四、学时分配表 学时安排 序号 内容 小计 理论课时 实验或习题课时 1 随机事件及其概率 8 2 10 2 随机变量及其数字特征 8 4 12 3 几种重要的概率分布 8 4 12 4 中心极限定理与参数估计 2 10 5 参数假设检验与线性回归分析 8 0 总计 40 14 54 五、主用教材及参考书 主用教材: 经济管理类 ·《概率与数理统计》第二版主编:周誓达,出版社:中国人民大学出版社出 版时间:2010 参考书: 1、《概率论与数理统计》(第二版)主编:吴传生出版社:高等教有出版社出版时间:2009 2、《概率论与数理统计》(第三版)主编:吴赣昌出版社:中国人民大学出版社出版时间: 2009 3、《概率论与数理统计》(第三版)主编:龙永红出版社:高等教有出版社出版时间:2009 4、《概率与数理统计》习题详解,主编:孙洪祥柳金甫出版社:清华大学出版社出版时间 2007
第二节 单个正态总体参数的假设检验 第三节 两个正态总体参数的假设检验 第四节 一元线性回归分析 四、学时分配表 学 时 安 排 序号 内 容 理论课时 实验或习题课时 小计 1 随机事件及其概率 8 2 10 2 随机变量及其数字特征 8 4 12 3 几种重要的概率分布 8 4 12 4 中心极限定理与参数估计 8 2 10 5 参数假设检验与线性回归分析 8 2 10 总 计 40 14 54 五、主用教材及参考书 主用教材: 经济管理类——《概率与数理统计》第二版 主编:周誓达,出版社:中国人民大学出版社 出 版时间:2010 参考书: 1、《概率论与数理统计》(第二版)主编:吴传生 出版社:高等教育出版社 出版时间:2009 2、《概率论与数理统计》(第三版)主编:吴赣昌 出版社:中国人民大学出版社 出版时间: 2009 3、《概率论与数理统计》(第三版)主编:龙永红 出版社:高等教育出版社 出版时间:2009 4、《概率与数理统计》习题详解,主编:孙洪祥 柳金甫出版社:清华大学出版社 出版时间: 2007