
《复变函数与积分变换》教学大纲 (2013版) 课程编码:1510312103 课程名称:复变函数与积分变换 学时/学分:48/3 先修课程:《高等数学》、《线性代数》、《概率论与数理统计》 适用专业:电子信息科学与技术等专业 开课教研室:大学数学教研室 执笔:赵守娟 审定:王仁举赵国喜
《复变函数与积分变换》教学大纲 (2013 版) 课程编码:1510312103 课程名称:复变函数与积分变换 学时/学分:48/3 先修课程:《高等数学》、《线性代数》、《概率论与数理统计》 适用专业:电子信息科学与技术等专业 开课教研室:大学数学教研室 执笔:赵守娟 审定:王仁举 赵国喜

《复变函数与积分变换》教学大纲 (2013版) 课程编码:1510312103 课程名称:复变函数与积分变换 学时/学分:48/3 先修课程:《高等数学》、《线性代数》、《概率论与数理统计》 适用专业:电子信息科学与技术等专业 开课教研室:大学数学教研室 执笔: 审定
《复变函数与积分变换》教学大纲 (2013 版) 课程编码:1510312103 课程名称:复变函数与积分变换 学时/学分:48/3 先修课程:《高等数学》、《线性代数》、《概率论与数理统计》 适用专业:电子信息科学与技术等专业 开课教研室:大学数学教研室 执笔: 审定:

一、课程性质与任务 课程性质:该课程是电子信息科学与技术等专业的一门专业基础课 课程任务:使学生学习复变函数的基本知识、解析函数的基本理论、复变函数的积分性质和 计算方法、解析函数的泰勒展开式和洛朗展开式、留数及其在实积分中的应用,共形映射及分式 线性映射等方面的知识。 二、课程教学基本要求 1.理解复变函数中的概念、理论和方法,掌握其与实变函数的共同点和不同点: 2.掌握复变函数导数和积分概念以及其计算方法,理解解析函数的概念和性质: 3.理解留数的概念,掌握和应用留数定理进行积分计算: 4.了解解析函数所构成的映射特性,理解共形映射的概念和应用: 5.掌握傅里叶变换和拉普拉斯变换的概念、性质和应用。 本课程共48学时,成绩考核形式:平时成绩(平时测验、作业、课党提问、课堂讨论等)(30 %)+期末成绩(闭卷考试)(70%),成绩评定采用百分制,60分为及格。 三、课程教学内容 第一章复数与复变函数 1.教学基本要求 熟练掌握复数的各种表示方法及其运算:了解区域的概念:理解复变函数的概念,知道复变 函数的极限和连续的概念。 2.要求学生掌握的基本概念、理论、原理 复数的各种表示方法及其运算:区域的概念:复变函数的概念:复变函数的极限和连续的概 念. 3.教学重点和难点 教学重点是复数的三种表示:区域与连通性:复变函数的极限。教学难点是扩充复平面,复 数开方和多值函数 4.教学内容 第一节 复数 第二节 复数的三角表示 第三节 平面点集的一般概念 第四节 无穷大与复球面 第五节 复变函数 第二章 解析函数 1.教学基本要求 理解复变函数的导数概念及解析函数的概念及解析函数与柯西一黎曼方程的联系,了解某些
一、课程性质与任务 课程性质:该课程是电子信息科学与技术等专业的一门专业基础课。 课程任务:使学生学习复变函数的基本知识、解析函数的基本理论、复变函数的积分性质和 计算方法、解析函数的泰勒展开式和洛朗展开式、留数及其在实积分中的应用,共形映射及分式 线性映射等方面的知识。 二、课程教学基本要求 1.理解复变函数中的概念、理论和方法,掌握其与实变函数的共同点和不同点; 2.掌握复变函数导数和积分概念以及其计算方法,理解解析函数的概念和性质; 3.理解留数的概念,掌握和应用留数定理进行积分计算; 4.了解解析函数所构成的映射特性,理解共形映射的概念和应用; 5.掌握傅里叶变换和拉普拉斯变换的概念、性质和应用。 本课程共 48 学时,成绩考核形式:平时成绩(平时测验、作业、课堂提问、课堂讨论等)(30 %)+期末成绩(闭卷考试)(70%),成绩评定采用百分制,60 分为及格。 三、课程教学内容 第一章 复数与复变函数 1.教学基本要求 熟练掌握复数的各种表示方法及其运算;了解区域的概念;理解复变函数的概念,知道复变 函数的极限和连续的概念。 2.要求学生掌握的基本概念、理论、原理 复数的各种表示方法及其运算;区域的概念;复变函数的概念;复变函数的极限和连续的概 念。 3.教学重点和难点 教学重点是复数的三种表示;区域与连通性;复变函数的极限。教学难点是扩充复平面, 复 数开方和多值函数 4.教学内容 第一节 复数 第二节 复数的三角表示 第三节 平面点集的一般概念 第四节 无穷大与复球面 第五节 复变函数 第二章 解析函数 1.教学基本要求 理解复变函数的导数概念及解析函数的概念及解析函数与柯西—黎曼方程的联系,了解某些

初等解析函数的基本性质:了解调和函数与解析函数的关系,掌握从解析函数的实(虚)部求其 虚(实部)的方法。 2.要求学生掌握的基本概念、理论、原理 复变函数的导数概念:解析函数的概念:柯西一黎曼方程:调和函数与解析函数的关系:从 解析函数的实(虚)部求其虚(实部)。 3.教学重点和难点 教学重点是理解函数解析的充要条件,掌握初等函数及其计算法。教学难点是多值解析函数 单值分支问颗,柯西-一一黎品条件 4.教学内容 第一节 解析函数的概念 第二节 解析函数和调和函数的关系 第三节 初等函数 第三章 复变函数的积分 1.教学基本要求 理解积分的定义,了解其性质,会求积分:掌握柯西定理、复合闭路定理、柯西积分公式和 高阶导数公式。 2.要求学生掌握的基本概念、理论、原理 复积分的定义,柯西定理、复合闭路定理、柯西积分公式和高阶导数公式。 3.教学重点和难点 教学重点是理解柯西积分基本定理,掌握柯西积分公式和解析函数的高阶导数公式。教学难 点是多连通区域上的柯西积分定理,解析函数的无穷可微性。 4.教学内容 第一节 复积分的概念 第二节 柯西积分定理 第三节 柯西积分公式 第四节 解析函数的高阶导数 第四章 解析函数的级数表示 1.教学基本要求 理解复数顶级数、幂级数收敛、发散概念,了解幂级数的本性质,了解收敛半径的求法: 掌握简单函数在不同圆环域内展开为罗朗级数的间接方法。 2.要求学生掌握的基本概念、理论、原理 复数项级数、幂级数收敛、发散概念,幂级数的基本性质,收敛半径的求法,简单函数在不 同圆环域内展开为罗朗级数
初等解析函数的基本性质;了解调和函数与解析函数的关系,掌握从解析函数的实(虚)部求其 虚(实部)的方法。 2.要求学生掌握的基本概念、理论、原理 复变函数的导数概念;解析函数的概念;柯西—黎曼方程;调和函数与解析函数的关系;从 解析函数的实(虚)部求其虚(实部)。 3.教学重点和难点 教学重点是理解函数解析的充要条件,掌握初等函数及其计算法。教学难点是多值解析函数 单值分支问题,柯西---黎曼条件。 4.教学内容 第一节 解析函数的概念 第二节 解析函数和调和函数的关系 第三节 初等函数 第三章 复变函数的积分 1.教学基本要求 理解积分的定义,了解其性质,会求积分;掌握柯西定理、复合闭路定理、柯西积分公式和 高阶导数公式。 2.要求学生掌握的基本概念、理论、原理 复积分的定义,柯西定理、复合闭路定理、柯西积分公式和高阶导数公式。 3.教学重点和难点 教学重点是理解柯西积分基本定理,掌握柯西积分公式和解析函数的高阶导数公式。教学难 点是 多连通区域上的柯西积分定理,解析函数的无穷可微性。 4.教学内容 第一节 复积分的概念 第二节 柯西积分定理 第三节 柯西积分公式 第四节 解析函数的高阶导数 第四章 解析函数的级数表示 1.教学基本要求 理解复数项级数、幂级数收敛、发散概念,了解幂级数的基本性质,了解收敛半径的求法; 掌握简单函数在不同圆环域内展开为罗朗级数的间接方法。 2.要求学生掌握的基本概念、理论、原理 复数项级数、幂级数收敛、发散概念,幂级数的基本性质,收敛半径的求法,简单函数在不 同圆环域内展开为罗朗级数

3.教学重点和难点 教学重点是收敛半径的求法,掌握复变函数展成泰勒级数和洛朗级数的方法。教学难点是级 数在收敛区间端点的敛散性,利用间接方法将函数展开成洛朗级数。 4.教学内容 第一节 复数项级数 第二节 复变函数项级数 第三节 泰勒级数 第四节 洛朗级数 第五章 留数及其应用 1.教学基本要求 理解孤立奇点及其分类、留数的概念及留数定理:熟练掌握极点处留数的求法及用留数求某 些定积分的计算方法。 2.要求学生掌握的基本概念、理论、原理 孤立奇点及其分类、留数的概念及留数定理:极点处留数的求法。 3.教学重点和难点 教学重点是奇点和极点的判断方法,利用留数定理计算留数:教学难点是扩充复平面上的留 数定理,利用留数定理计算几种类型的实积分。 4.教学内容 第一节 孤立奇点 第二节 留数 第三节 留数在定积分计算中应用 第六章 保形映射 1.教学基本要求 了解导数的几何意义及保角映射的概念:掌握分式线性映射的保圆性、保对称性等映射性质 及幂函数、指数函数的映射特点:会求一些简单区域(如半平面、角形域、圆域、带形域等)之 间的保形映射。 2.要求学生掌握的基本概念、理论、原理 导数的几何意义及保角映射的概念:分式线性映射的保圆性、保对称性等映射性质及幂函数 指数函数的映射特点: 3.教学重点和难点 教学重点是理解共形映射和分式线性映射的概念,竿握分式线性映射的性质。教学难点是掌 握分式线性映射的性质及唯一决定分式线性映射的条件。 4.教学内容
3.教学重点和难点 教学重点是收敛半径的求法,掌握复变函数展成泰勒级数和洛朗级数的方法。教学难点是级 数在收敛区间端点的敛散性,利用间接方法将函数展开成洛朗级数。 4.教学内容 第一节 复数项级数 第二节 复变函数项级数 第三节 泰勒级数 第四节 洛朗级数 第五章 留数及其应用 1.教学基本要求 理解孤立奇点及其分类、留数的概念及留数定理;熟练掌握极点处留数的求法及用留数求某 些定积分的计算方法。 2.要求学生掌握的基本概念、理论、原理 孤立奇点及其分类、留数的概念及留数定理;极点处留数的求法。 3.教学重点和难点 教学重点是奇点和极点的判断方法,利用留数定理计算留数;教学难点是扩充复平面上的留 数定理,利用留数定理计算几种类型的实积分。 4.教学内容 第一节 孤立奇点 第二节 留数 第三节 留数在定积分计算中应用 第六章 保形映射 1.教学基本要求 了解导数的几何意义及保角映射的概念;掌握分式线性映射的保圆性、保对称性等映射性质 及幂函数、指数函数的映射特点;会求一些简单区域(如半平面、角形域、圆域、带形域等)之 间的保形映射。 2.要求学生掌握的基本概念、理论、原理 导数的几何意义及保角映射的概念;分式线性映射的保圆性、保对称性等映射性质及幂函数、 指数函数的映射特点; 3.教学重点和难点 教学重点是理解共形映射和分式线性映射的概念,掌握分式线性映射的性质。教学难点是 掌 握分式线性映射的性质及唯一决定分式线性映射的条件。 4.教学内容

第一节 保形映射的概念 第二节 保形映射的基本问题 第三节 分式线性映射 第四节 几个初等函数构成的保形映射 第七章 傅里叶变换 1.教学基本要求 理解傅里叶变换的概念:了解6函数及其性质:堂挥傅里叶变换性质和卷积定理。 2.要求学生掌握的基本概念、理论、原理 傅里叶变换的概念:8函数及其性质:傅里叶变换性质和卷积定理 3.教学重点和难点 教学重点是理解Fourier积分、Fourier变换和Fourier逆变换的概念、性质,能熟练地 应用定义求函数的Fourier变换和Fourier逆变换及卷积:教学难点是函数卷积的定义、性质 及其计算。 4.教学内容 第一节 傅里叶变换的概念 第二节 单位脉冲函数(6函数) 第三节 傅里叶变换的性质 第八章 拉普拉斯变换 1.教学基本要求 理解拉氏变换概念:掌握拉氏变换的性质和卷积定理:会求有理函数的拉氏逆变换:掌握用 拉氏变换解微分方程的方法。 2.要求学生掌握的基本概念、理论、原理 拉氏变换概念:拉氏变换的性质和卷积定理:拉氏变换解微分方程 3.教学重点和难点 教学重点是Laplace变换、逆变换的概念、性质:卷积定义和卷积定理。教学重点是Laplace 变换存在定理、性质及应用,函数卷积的定义、性质及其计算,Laplace变换与Fourier变换的 区别、联系。 4教学内容 第一节 拉普拉斯变换的概念 第二节 拉氏变换的性质 第三节 拉普拉斯逆变换 第四节 拉氏变换的应用及综合举例 四、学时分配表
第一节 保形映射的概念 第二节 保形映射的基本问题 第三节 分式线性映射 第四节 几个初等函数构成的保形映射 第七章 傅里叶变换 1.教学基本要求 理解傅里叶变换的概念;了解δ函数及其性质;掌握傅里叶变换性质和卷积定理。 2.要求学生掌握的基本概念、理论、原理 傅里叶变换的概念;δ函数及其性质;傅里叶变换性质和卷积定理。 3.教学重点和难点 教学重点是理解 Fourier 积分、Fourier 变换和 Fourier 逆变换的概念、性质,能熟练地 应用定义求函数的 Fourier 变换和 Fourier 逆变换及卷积;教学难点是 函数卷积的定义、性质 及其计算。 4.教学内容 第一节 傅里叶变换的概念 第二节 单位脉冲函数(δ函数) 第三节 傅里叶变换的性质 第八章 拉普拉斯变换 1.教学基本要求 理解拉氏变换概念;掌握拉氏变换的性质和卷积定理;会求有理函数的拉氏逆变换;掌握用 拉氏变换解微分方程的方法。 2.要求学生掌握的基本概念、理论、原理 拉氏变换概念;拉氏变换的性质和卷积定理;拉氏变换解微分方程。 3.教学重点和难点 教学重点是 Laplace 变换、逆变换的概念、性质;卷积定义和卷积定理。教学重点是 Laplace 变换存在定理、性质及应用,函数卷积的定义、性质及其计算,Laplace 变换与 Fourier 变换的 区别、联系。 4.教学内容 第一节 拉普拉斯变换的概念 第二节 拉氏变换的性质 第三节 拉普拉斯逆变换 第四节 拉氏变换的应用及综合举例 四、学时分配表
学时安排 序号 内容 小计 理论课时 实验或习题课 1 复数与复变函数 4 2 6 2 解析函数 4 4 3 复变函数的积分 4 2 6 4 级数 2 2 5 留数 6 6 共形映射 4 4 7 傅里叶变换 8 2 10 8 拉普拉斯变换 10 总计 38 10 48 五、主用教材及参考书 主用教材: 复变函数与积分变换(第三版),华中科技大学数学系。北京:高等教有出版社,2003 参考书: 1.复变函数(第三版)主编:钟玉泉出版社:高等教有出版社,出版时间:2003 2.复变函数学习指导书主编:钟玉泉出版社:高等教有出版社,出版时间:2003 3.高等数学(上、下册)(第六版)主编:同济大学应用数学系出版社:高等教育出版社出 版时间:2012
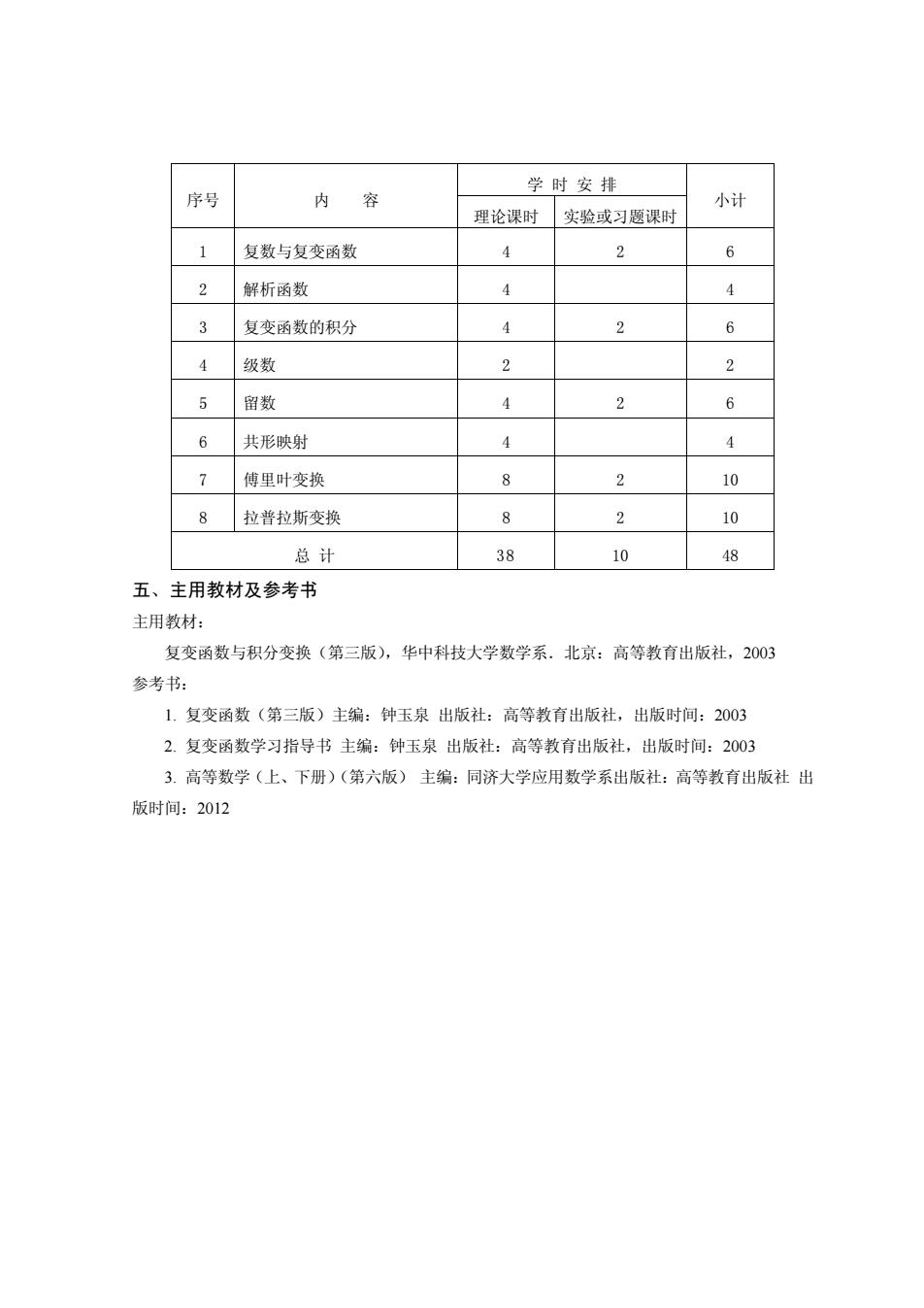
学 时 安 排 序号 内 容 理论课时 实验或习题课时 小计 1 复数与复变函数 4 2 6 2 解析函数 4 4 3 复变函数的积分 4 2 6 4 级数 2 2 5 留数 4 2 6 6 共形映射 4 4 7 傅里叶变换 8 2 10 8 拉普拉斯变换 8 2 10 总 计 38 10 48 五、主用教材及参考书 主用教材: 复变函数与积分变换(第三版),华中科技大学数学系.北京:高等教育出版社,2003 参考书: 1. 复变函数(第三版)主编:钟玉泉 出版社:高等教育出版社,出版时间:2003 2. 复变函数学习指导书 主编:钟玉泉 出版社:高等教育出版社,出版时间:2003 3. 高等数学(上、下册)(第六版) 主编:同济大学应用数学系出版社:高等教育出版社 出 版时间:2012