
第五章 大数定律及中心极限定理 §5.1大数定律 §5.2, 中心极限定理
第五章 大数定律及中心极限定理 §5.1 大数定律 §5.2 中心极限定理

◆概率论与数理统计是研究随机现象统计规律性的 学科。而随机现象的统计规律性是在相同条件下 进行大量重复试验呈现出来的。 ◆例如,在概率的统计定义中,曾提到一事件发生 的频率具有稳定性,即事件发生的频率趋于事件 发生的概率:当试验次数无限增大时,事件发生 的频率在某种收敛意义下逼近一定数。这就是最 早的大数定律。 ◆一般的大数定律讨论n个随机变量的平均值的稳 定性
概率论与数理统计是研究随机现象统计规律性的 学科。而随机现象的统计规律性是在相同条件下 进行大量重复试验呈现出来的。 例如,在概率的统计定义中,曾提到一事件发生 的频率具有稳定性,即事件发生的频率趋于事件 发生的概率:当试验次数无限增大时,事件发生 的频率在某种收敛意义下逼近一定数。这就是最 早的大数定律。 一般的大数定律讨论n个随机变量的平均值的稳 定性

频率“稳定于”概率应从可能性角度来解释,即 对于y8>0.只要流分大份-p心产6发在的可能 性很小,而且随着的增大,越来越小 台房心c- 这种收敛性称为“依概率收敛”!
频率“稳定于”概率应从可能性角度来解释, 即 0 , , A n n p n n 对于 只要 充分大 发生的可能 性很小,而且随着 的增大,越来越小. 这种收敛性称为“依概率收敛”! lim 0. A n n P p n 3

§5.1大数定律 定义1 设Y,Y2,Yn…为一随机变量序列,是常数, 若对任意正数ε,有 lim P(Y -a<&)=1 n-→o0 则称随机变量序列Y,Y2,,Yn,…依概率收敛于4, 记为: Yy-Pxa 性质:设X,P→,卫nP→h,gk,)在点(a,b)连续, 则g(Xn,Yn)P→g(a,b)
§5.1 大数定律 lim {| | } 1 n n P Y a Y a n P g( ) g(a,b) n n P X ,Y 性质:设 P , X a n Y b n P 则称随机变量序列Y1 , Y2 ,…,Yn , ... 依概率收敛于a , 记为: 若对任意正数,有 定义1 设Y1 , Y2 …,Yn ,...为一随机变量序列,a是常数, , g(x, y)在点(a, b)连续, 则

定理1(切比雪夫定理的特殊情况)设随机变量序 列X,X2,Xm,…相互独立,且具有相同的数学期望 和方差:EX)=μ,DX)=o2(k=1,2),则对任意 的ε>0,有 P2x<-1 即 i= 提示:利用切比雪夫不等式证, 此定理表明:相互独立具有相同期望和方差的随机变 量X,X2,,X的算术平均值依概率收敛于其数学期 望值山
定理1 (切比雪夫定理的特殊情况)设随机变量序 列 X1 ,X2 ,…,Xn , ...相互独立,且具有相同的数学期望 和方差: 1 1 n P i i X X n E(Xk )=,D(Xk )=2 (k=1,2,...) , 则对任意 此定理表明: 相互独立具有相同期望和方差的随机变 量X1 , X2 , …, Xn的算术平均值依概率收敛于其数学期 望值 . 1 1 lim X 1 n i n i P n 即 的 > 0,有 提示:利用切比雪夫不等式证
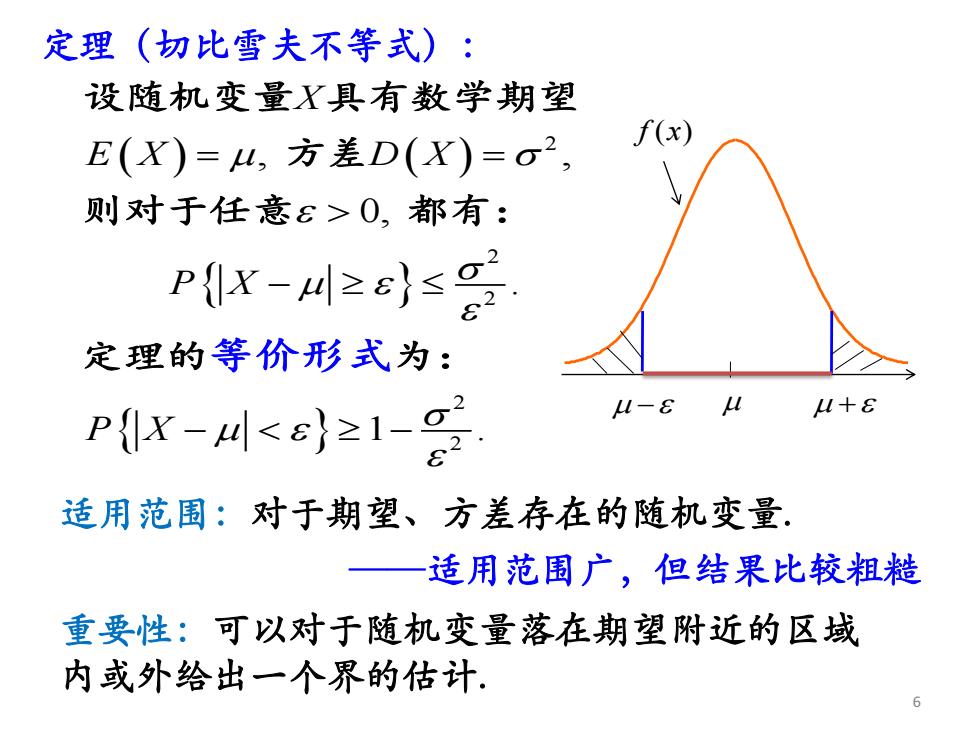
定理 (切比雪夫不等式): 设随机变量X具有数学期望 (x E(X)=4,方差D(X)=o2, 则对于任意8>0,都有: Px-川≥e}s 定理的等价形式为: Pr-4<≥1- u-8 +8 82 适用范围:对于期望、方差存在的随机变量, —适用范围广,但结果比较粗糙 重要性:可以对于随机变量落在期望附近的区域 内或外给出一个界的估计
2 2 2 2 2 , , 0, . 1 . X E X D X P X P X 设随机变量 具有数学期望 方差 则对于任意 都有: 定理的等价形式为: 定理(切比雪夫不等式): f x( ) 6 适用范围:对于期望、方差存在的随机变量. ——适用范围广,但结果比较粗糙 重要性:可以对于随机变量落在期望附近的区域 内或外给出一个界的估计

定理2(贝努力大数定律)设n4是n次独立重复 试验中A发生的次数.p是事件A在每次试验中发 生的概率,则对任意ε>0,有 怡小-1一÷ 1-→0 此定理表明: nAP→P(A),(n-→o) n 即:事件A发生的频率依概率收敛于事件的概率p, 这个定理以严格的数学形式表达了频率的稳定性
定理2 (贝努力大数定律)设nA是n 次独立重复 试验中A发生的次数. p 是事件A在每次试验中发 生的概率, 则对任意 > 0,有 1 1 lim 1 X p n P n k k n - 证: lim 1 p n nA n P - lim 0 p n nA n P - nA X1 X2 Xn 因而 E(Xk )=p,D(Xk )=p(1-p), (k=1,2,...),由定理1, 因为 n ~ b(n, p), A 有 lim 1 p n n P A n 即:事件A发生的频率依概率收敛于事件的概率 即 - p . 这个定理以严格的数学形式表达了频率的稳定性. P(A),(n ) n 此定理表明: nA P

定理3(辛钦定理) 设随机变量序列X1,X2,X… 相互独立且同分布,数学期望:E(X)=μ,则对任 意正数ε,有 宫,- (证明略) 注意:此处未指定变量的方差 [注] >贝努力大数定律就是频率稳定性的理论依据. 因而在实际应用中,当试验次数很大时,往往 用事件发生的频率来代替事件的概率. >贝努力大数定律是辛钦定理的特殊情况
贝努力大数定律就是频率稳定性的理论依据. 因而在实际应用中,当试验次数很大时,往往 用事件发生的频率来代替事件的概率. X 1 1 lim P 1 n i i n n 定理3(辛钦定理)设随机变量序列X1 ,X2 ,…,Xn ,... 相互独立且同分布,数学期望:E(Xk )=,则对任 意正数,有 贝努力大数定律是辛钦定理的特殊情况. [注] (证明略) 注意:此处未指定变量的方差

§5.2中心极限定理 问题的提出: 有许多随机变量,它们是由大量的相互 独立的随机变量的综合影响所形成的,而其 中每个个别的因素作用都很小,这种随机变 量往往服从或近似服从正态分布,或者说它 的极限分布是正态分布,中心极限定理正是 从数学上论证了这一现象。 它在长达两个世纪的时期内曾是概率论 研究的中心课题
10 问题的提出: 有许多随机变量,它们是由大量的相互 独立的随机变量的综合影响所形成的,而其 中每个个别的因素作用都很小,这种随机变 量往往服从或近似服从正态分布,或者说它 的极限分布是正态分布,中心极限定理正是 从数学上论证了这一现象。 它在长达两个世纪的时期内曾是概率论 研究的中心课题. §5.2 中心极限定理

X X1+X2 n个独立 1.5 1.5 同分布的 0.5 均匀分布 0.5 随机变量 X+X+X3 X,+X2+X3+X4 的和: 0.8 0.8 0.6 0 0 2 -0.20 -02 11
X1 X X 1 2 X X X 1 2 3 X X X X 1 2 3 4 n个独立 同分布的 均匀分布 随机变量 的和: 11