
实用大众线性代数 (MATLAB版)
实用大众线性代数 (MATLAB版)

本书的主要分章目录 ·序言 第1章 线性方程组与矩阵 ·第2章 矩阵运算及其应用 ·第3章行列式 。第4章平面和空间向量 ·第5章 线性变换及其特征 ·第6章在后续课程中的应用举例 ·附录A MATLAB的矩阵代数和作图初步 ·附录B,C本书中应用实例索引
本书的主要分章目录 • 序言 • 第1章 线性方程组与矩阵 • 第2章 矩阵运算及其应用 • 第3章 行 列 式 • 第4章 平面和空间向量 • 第5章 线性变换及其特征 • 第6章 在后续课程中的应用举例 • 附录A MATLAB的矩阵代数和作图初步 • 附录B,C 本书中应用实例索引

序言 线性代数改革的两大动力 ·“需求牵引”:线性代数的应用扩大到愈来愈多的新领域, 。 “技术推动”:计算机硬软件的飞速发展,给以应用作为 方向改革提供了机遇。 本书的三个特点: 0 “实用化”指的是本书以工科的后续课及未来工程的需求 为标准安排内容,附录B,C中列出的60个应用实例表明了 本书的实用价值: “现代化”指的是用软件MATLAB来解决问题,不靠笔算; “大众化”指的是书中采用了最少、最浅而又足够的理论, 既能解决实际问题,又便于向大众普及
序 言 线性代数改革的两大动力 • “需求牵引”:线性代数的应用扩大到愈来愈多的新领域, • “技术推动”:计算机硬软件的飞速发展,给以应用作为 方向改革提供了机遇。 本书的三个特点: • “实用化”指的是本书以工科的后续课及未来工程的需求 为标准安排内容,附录B,C中列出的60个应用实例表明了 本书的实用价值; • “现代化”指的是用软件MATLAB来解决问题,不靠笔算; • “大众化”指的是书中采用了最少、最浅而又足够的理论, 既能解决实际问题,又便于向大众普及

第1章线性方程组与矩阵 。1.1概述 ·1.2二、三元线性方程组解的几何意 义 ·1.3高斯消元法与阶梯形方程组 ·1.4矩阵及矩阵的初等变换 ·1.5行阶梯形矩阵的用途 ·1.6应用实例
第1章 线性方程组与矩阵 • 1.1 概 述 • 1.2 二、三元线性方程组解的几何意 义 • 1.3 高斯消元法与阶梯形方程组 • 1.4 矩阵及矩阵的初等变换 • 1.5 行阶梯形矩阵的用途 • 1.6 应 用 实 例
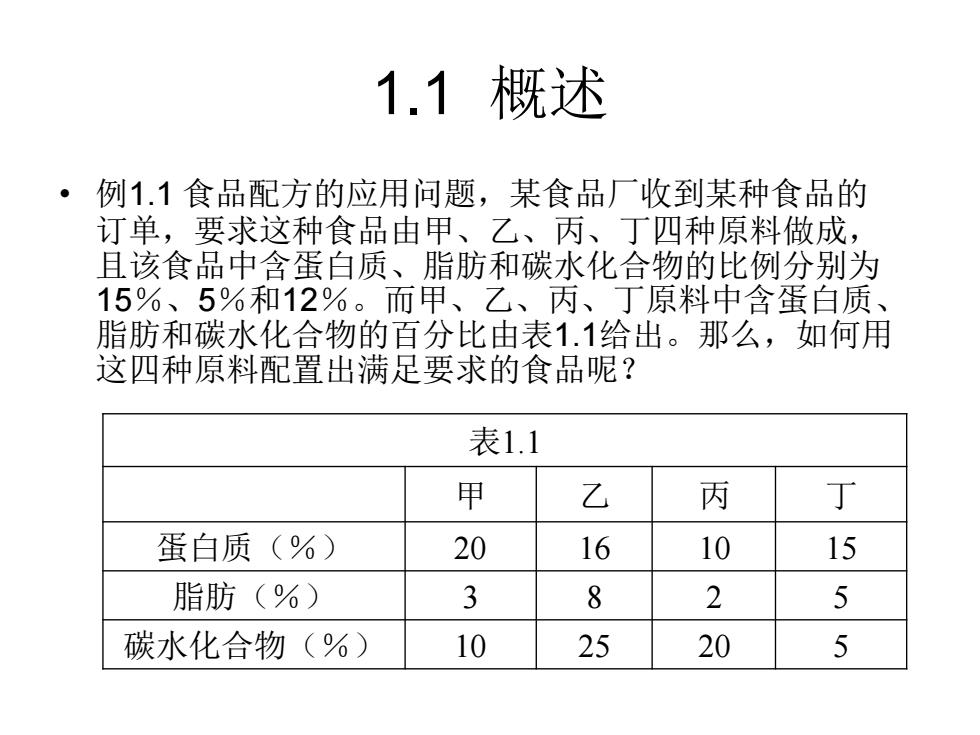
1.1概述 ·例1.1食品配方的应用问题,某食品厂收到某种食品的 订单,要求这种食品由甲、乙、丙、丁四种原料做成, 且该食品中含蛋白质、脂肪和碳水化合物的比例分别为 15%、5%和12%。而甲、乙、丙、丁原料中含蛋白质、 脂肪和碳水化合物的百分比由表1.1给出。那么,如何用 这四种原料配置出满足要求的食品呢? 表1.1 甲 乙 丙 丁 蛋白质(%) 20 16 10 15 脂肪(%) 3 8 2 5 碳水化合物(%) 10 25 20 5
1.1 概述 • 例1.1 食品配方的应用问题,某食品厂收到某种食品的 订单,要求这种食品由甲、乙、丙、丁四种原料做成, 且该食品中含蛋白质、脂肪和碳水化合物的比例分别为 15%、5%和12%。而甲、乙、丙、丁原料中含蛋白质、 脂肪和碳水化合物的百分比由表1.1给出。那么,如何用 这四种原料配置出满足要求的食品呢? 表1.1 甲 乙 丙 丁 蛋白质(%) 20 16 10 15 脂肪(%) 3 8 2 5 碳水化合物(%) 10 25 20 5

例1.1食品配方问题 x1+x2+X3+x4=1 20x+16x2+10x3+15x4=15 (1.1.1D 3x1+8x2+2x3+5x4=5 10x1+25x2+20x3+5x4=12 。方程组(1.1.1)中,左端是未知量x1,x2,x3,x4的 乘以常数后的叠加,也称为它们的线性组合。右 端是常数,这样的方程组称为线性方程组。对于 本问题,所找到的方程组的解,必须满足 ×1,X2,X3,X4≥0,才是合理解
例1.1 食品配方问题 • 方程组(1.1.1)中,左端是未知量x1,x2,x3,x4的 乘以常数后的叠加,也称为它们的线性组合。右 端是常数,这样的方程组称为线性方程组。对于 本问题,所找到的方程组的解,必须满足 x1,x2,x3,x4 ≥0,才是合理解。 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 20 16 10 15 15 1.1.1 3 8 2 5 5 10 25 20 5 12 x x x x x x x x x x x x x x x x + + + = + + + = + + + = + + + = ( )

线性代数的任务 有多解 解集的性质 有解 线性方程组 有唯一解 有合理解 解的情况 无解 找出近似解 无合理解
线性代数的任务

1.2线性方程组解的几何意义 •例1.2二元线性方程组解法 ow-小- x2=2 x1-2x3=-1 ·题(a)可以由下而上地回代解出x2=2,及x1=3,这是 解线性方程组的规范方法。 ·题(b)则无解。 。 题(©)有无穷多解。其几何解释见下图
1.2 线性方程组解的几何意义 1 2 1 2 1 2 2 2 1 2 2 1 2 1 ( ) 3 3 2 x x x x a x x r r r x − = − − = − − + = = + = 1 2 1 2 1 2 2 2 1 1 2 2 1 2 1 ( ) 2 3 0 0 2 x x x x b x x r r r x x − = − − = − − + = = + + = • 题(a)可以由下而上地回代解出x2=2,及x1=3,这是 解线性方程组的规范方法。 • 题(b)则无解。 • 题(c)有无穷多解。其几何解释见下图。 •例1.2 二元线性方程组解法
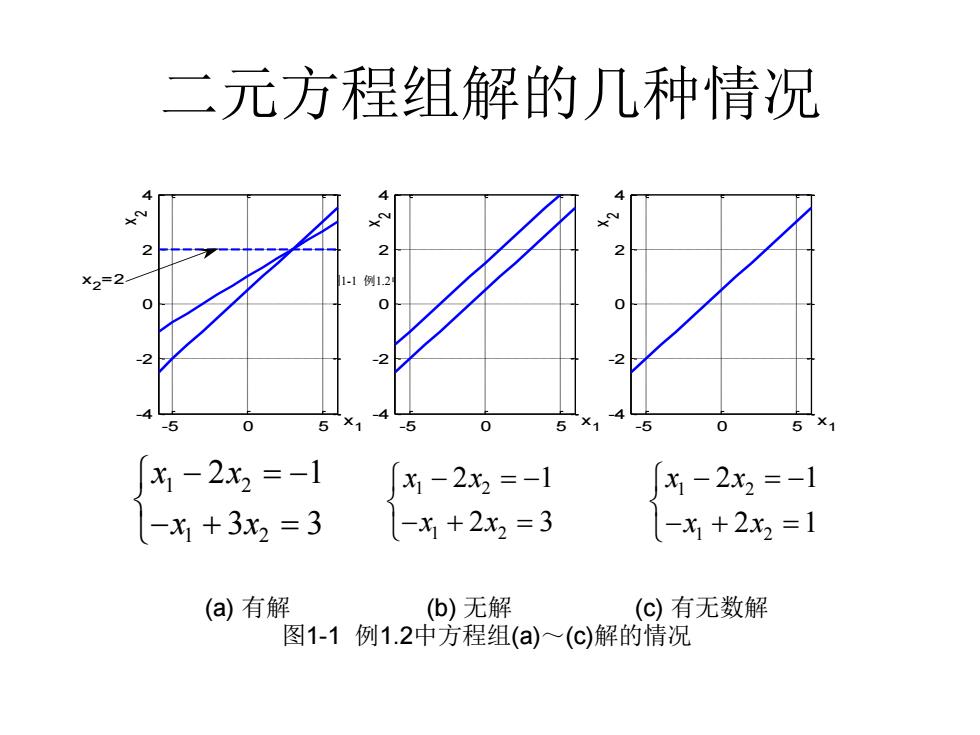
二元方程组解的几种情况 2 2 ×2=2 例1.2 0 5×1 x1-2x2=-1 x1-2x2=-1 1-2x2=-1 -x1+3x2=3 -x1+2x2=3 -x+2x2=1 (a)有解 (b)无解 (c)有无数解 1-1例1.2中方程组(a)~(c)解的情况
二元方程组解的几种情况 (a) 有解 (b) 无解 (c) 有无数解 图1-1 例1.2中方程组(a)~(c)解的情况 -5 0 5 -4 -2 0 2 4 x 1 x 2 -5 0 5 -4 -2 0 2 4 x 1 x 2 -5 0 5 -4 -2 0 2 4 x 1 x 2 x 2 = 2 (a) 有解 (b) 无解 (c) 有无数解 图1-1 例1.2中方程组(a)~(c)解的情况 1 2 1 2 2 1 3 3 x x x x − = − − + = 1 2 1 2 2 1 2 3 x x x x − = − − + = 1 2 1 2 2 1 2 1 x x x x − = − − + =

超定二元方程组的近似解 x1+x2=1 5 水1-x2=3 1+2-1 -X1+2x2=-3 (07-43) X123 …223.0 0 5 三个方程,只有两个变量。它们所对应的三根直线并不 共点,即方程组不相容,称为超定方程组。它没有精确 解,但有近似解一最小二乘解
超定二元方程组的近似解 1 2 1 2 1 2 1 3 2 3 x x x x x x + = − = − + = − 三个方程,只有两个变量。它们所对应的三根直线并不 共点,即方程组不相容,称为超定方程组。它没有精确 解,但有近似解——最小二乘解