西安电子科技大学：《实用大众线性代数》课程PPT教学课件（MATLAB版）第2章 矩阵运算及其应用

第2章矩阵运算及其应用 把多个线性系统相互联接，构成更大、 更复杂的系统，或者化简为较小的简单 系统，是线性代数要完成的重要任务， 这就需要建立矩阵代数的理论和算法

第2章 矩阵运算及其应用 把多个线性系统相互联接，构成更大、 更复杂的系统，或者化简为较小的简单 系统，是线性代数要完成的重要任务， 这就需要建立矩阵代数的理论和算法

矩阵运算离不开计算机 ·矩阵可以有规则地组织大量的数据。比如1000行 1000列的矩阵，包含了100万个元素，这种数据 组织的方法，特别适合于计算机的存储器硬件。 同时，计算机是对海量数据进行成批处理的。因 此我们要为矩阵的运算建立一些规则，使得两个 矩阵的运算得出另一个更大的有特定意义的矩阵。 熟悉了这些规则，就可以方便地对实际问题建模。 将这类运算编成子程序，甚至按照矩阵的运算法 则来设计计算机硬件，从而大大提高编程和计算 的效率

矩阵运算离不开计算机 • 矩阵可以有规则地组织大量的数据。比如1000行 1000列的矩阵，包含了100万个元素，这种数据 组织的方法，特别适合于计算机的存储器硬件。 同时，计算机是对海量数据进行成批处理的。因 此我们要为矩阵的运算建立一些规则，使得两个 矩阵的运算得出另一个更大的有特定意义的矩阵。 熟悉了这些规则，就可以方便地对实际问题建模。 将这类运算编成子程序，甚至按照矩阵的运算法 则来设计计算机硬件，从而大大提高编程和计算 的效率

2.1矩阵的加减乘法 四超市上下两个半年的销售清单 上半年销售表 大米 面粉 食油 超市一 150 250 50 超市二 250 500 100 超市三 300 700 120 超市四 450 850 80 下半年销售表 大米 面粉 食油 超市一 180 350 60 超市二 300 550 120 超市三 350 850 150 超市四 500 850 100

2.1 矩阵的加减乘法 四超市上下两个半年的销售清单 上半年销售表 大米 面粉 食油 超市一 150 250 50 超市二 250 500 100 超市三 300 700 120 超市四 450 850 80 下半年销售表 大米 面粉 食油 超市一 180 350 60 超市二 300 550 120 超市三 350 850 150 超市四 500 850 100

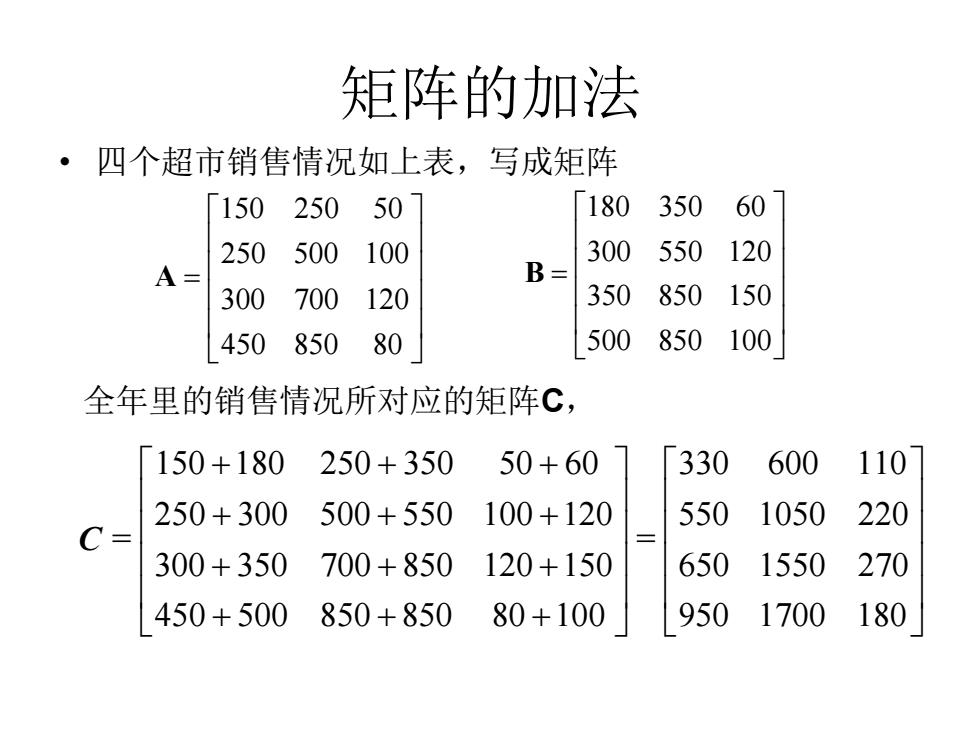
矩阵的加法 ·四个超市销售情况如上表，写成矩阵 150 250 50 180 350 60 250 500 100 300 550 120 A= B= 300 700 120 350 850 150 450 850 80 500 850 100 全年里的销售情况所对应的矩阵C, 150+180250+350 50+60 330 600 110 250+300500+550100+120 550 1050 220 C= 300+350700+850120+150 650 1550 270 450+500850+850 80+100 9501700 180

矩阵的加法 • 四个超市销售情况如上表，写成矩阵 150 180 250 350 50 60 330 600 110 250 300 500 550 100 120 550 1050 220 = = 300 350 700 850 120 150 650 1550 270 450 500 850 850 80 100 950 1700 180     + + +     + + +         + + +         + + + C 150 250 50 250 500 100 300 700 120 450 850 80     =         A 180 350 60 300 550 120 350 850 150 500 850 100     =         B 全年里的销售情况所对应的矩阵C

矩阵的数乘 ·例2.2 甲、乙、丙三位同学在期末考试中，4门课程的成绩分 别由表2.3给出，而他们的平时成绩则由表2.4给出，若期末考试成 绩占总成绩的90%，而平时成绩占10%，请用矩阵运算来表述这 三名同学的总成绩。 ·解：用矩阵A、B分别表示期末成绩和平时成绩： 85 85 6598 90 70 80 92 A= 75 95 7095 B= 80 9082 92 80 7076 92」 85 7590 90 · 总成绩为： 85.583.5 66.5 97.4 ·C=0.9A+0.1B= 75.594.5 71.294.7 80.570.577.491.8

矩阵的数乘 • 例2.2 甲、乙、丙三位同学在期末考试中，4门课程的成绩分 别由表2.3给出，而他们的平时成绩则由表2.4给出，若期末考试成 绩占总成绩的90％，而平时成绩占10％，请用矩阵运算来表述这 三名同学的总成绩。 • 解：用矩阵A、B分别表示期末成绩和平时成绩： • 总成绩为： • C=0.9A+0.1B= 85 85 65 98 75 95 70 95 80 70 76 92     =       A 90 70 80 92 80 90 82 92 85 75 90 90     =       B 85.5 83.5 66.5 97.4 75.5 94.5 71.2 94.7 80.5 70.5 77.4 91.8          

数乘的定义及运算规则 数λ与矩阵 的乘积，简称数乘，记作λA或AW, 规定为 A=(a) xn 2a11 2a12 九A=A几= 2a21 2d22 2C, Aa a 矩阵的加法和数乘统称为矩阵的线性运算，运算规律相同： (1)加法交换律：A+B=B+A (2)加法结合律：A+(B+C)=(A+B)+C (3)数乘结合律：（2)A=(uA)=(2A (4)数乘分配律 (A+B)=九A+B

数乘的定义及运算规则 数λ与矩阵 的乘积，简称数乘，记作λA或Aλ ， 规定为 矩阵的加法和数乘统称为矩阵的线性运算，运算规律相同： （1）加法交换律: A+B=B+A （2）加法结合律: A+(B+C)=(A+B)+C （3）数乘结合律： （4）数乘分配律 ( ij)m n a  A = 11 12 1 21 22 2 1 2 n n m m mn a a a a a a a a a                = =           A A(     ) A A A = = ( ) ( )    (A B A B + ) = +

矩阵的乘法 例2.3有甲、乙、丙、丁4个服装厂， 表2.5服装厂的月产量 一个月的产量情况由表2.5给出， 甲 乙 丙 丁 若甲厂生产8个月，乙厂生产10 个月，丙厂生产5个月，而丁厂生 帽 20 4 2 7 产9个月，则共生产帽子、衣服、 衣 10 18 6 裤子各多少？用矩阵来描述。 裤 5 7 16 3 8 20 77 10 A- 10 18 5 6 b= 5 J 7 16 3 9 20×8+4×10+2×5+7×9 273 C=A*b= 10×8+18×10+5×5+6×9 339 5×8+7×10+16×5+3×9 217

矩阵的乘法 例2.3 有甲、乙、丙、丁4个服装厂， 一个月的产量情况由表2.5给出， 若甲厂生产8个月，乙厂生产10 个月，丙厂生产5个月，而丁厂生 产9个月，则共生产帽子、衣服、 裤子各多少？用矩阵来描述。 表2.5 服装厂的月产量 甲 乙 丙 丁 帽 20 4 2 7 衣 10 18 5 6 裤 5 7 16 3 20 4 2 7 10 18 5 6 5 7 16 3     =       A 8 10 5 9     =           b 20 8 4 10 2 5 7 9 273 10 8 18 10 5 5 6 9 339 5 8 7 10 16 5 3 9 217      +  +  +      =  +  +  +  =              +  +  +  C = A * b

矩阵乘法定义 定义2.3设A是m×s矩阵，B是sXn矩阵，那么矩阵和矩阵的乘积 是一个m×n矩阵C,其中C的各个元素为： C=∑akbg=an4,+a2b2,+…+abg k=1 (2.1.3) (i=1,2,…,mj=1,2,…,n) ·记作C=A*B。称左矩阵的列数和右矩阵的行数s为内阶数，由定义 知，只有当它们的内阶数相等时，两个矩阵才能相乘。 a11 a2…4s … C Cui Cin .: W b2 a12 ais . Ci Cin … bsi am Cml Cmj ·Cmn 按定义，矩阵乘法不满足交换律

矩阵乘法定义 • 定义2.3 设A是m×s矩阵，B是s×n矩阵，那么矩阵和矩阵的乘积 是一个m×n矩阵C，其中C的各个元素为： • （2.1.3） • 记作C=A*B。称左矩阵的列数和右矩阵的行数s为内阶数，由定义 知，只有当它们的内阶数相等时，两个矩阵才能相乘。 按定义，矩阵乘法不满足交换律。 1 1 2 2 1 s ij ik kj i j i j is sj k c a b a b a b a b = = = + + +  (i m j n = = 1,2, , ; 1,2, , ) 11 12 1 11 1 1 11 1 1 21 2 2 1 2 1 1 1 1 1 s j n j n j n i i i s i i j i n s s j s n m m m s m m j m n a a a c c c b b b b b b a a a c c c b b b a a a c c c                   =                    

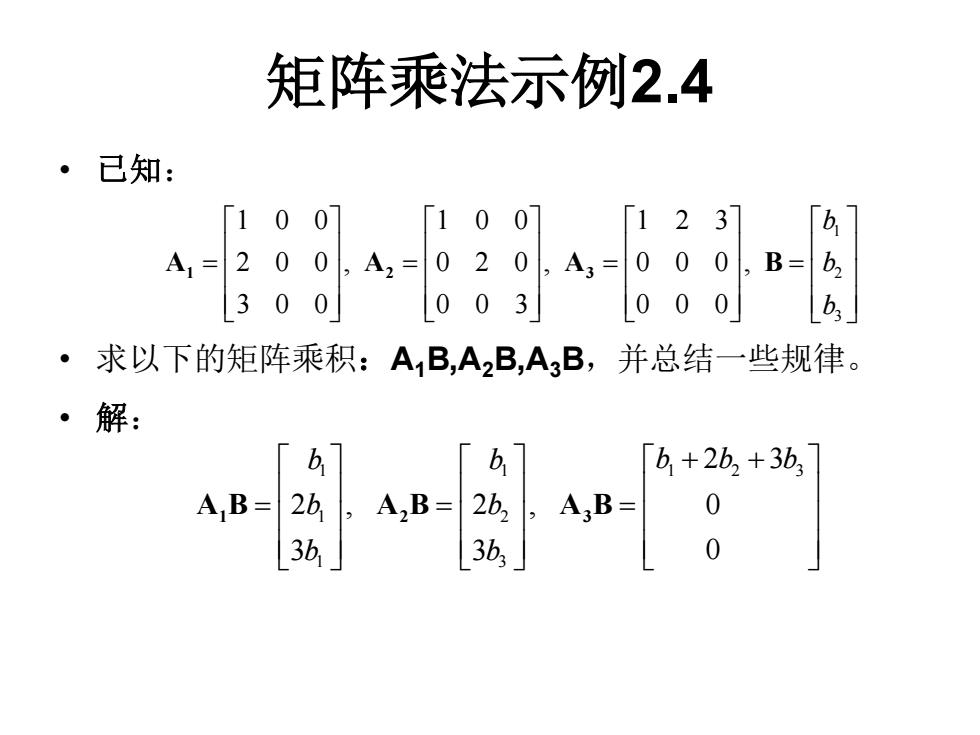
矩阵乘法示例2.4 ·已知： 「100 100 「123 「b A1=200, A2=020,A3= 0 0 0,B= b2 300 0 03 0 0 0 b3」 求以下的矩阵乘积：AB,A2B,A3B,并总结一些规律。 ·解： b b b+2b2+3b A,B=2b 1，A2B=1 0 [3b

矩阵乘法示例2.4 • 已知： • 求以下的矩阵乘积：A1B,A2B,A3B，并总结一些规律。 • 解： 1 2 3 1 0 0 1 0 0 1 2 3 2 0 0 , 0 2 0 , 0 0 0 , 3 0 0 0 0 3 0 0 0 b b b                 = = = =                         A A A B 1 2 3 1 1 1 2 3 1 2 1 3 2 3 2 , 2 , 0 3 3 0 b b b b b b b b b       + +       = = =                   A B A B A B 1 2 3

定义2.4 线性变换 ·对于向量Y=[y1,y2,,ym],若它们能由变量X=[x,x2,…,xn] 线性表示，即有： y=a+a2x2+.+ainxn y2=a21x1+a222+…+a2nXm (2.1.4) ym =amx +am2x2++amnxn 则称此关系式为变量X到变量Y的线性变换。可以写成输 出向量Y等于系数矩阵A左乘输入向量X: a11 a12 … an 21 Y= a22 02 =AX（2.1.5) ym am am2 Xn

定义2.4 线性变换 • 对于向量 ，若它们能由变量 线性表示，即有： （2.1.4） • 则称此关系式为变量Ｘ到变量Ｙ的线性变换。可以写成输 出向量Y等于系数矩阵A左乘输入向量X： （2.1.5） 1 11 1 12 2 1 2 21 1 22 2 2 1 1 2 2 n n n n m m m mn n y a x a x a x y a x a x a x y a x a x a x  = + + +   = + + +     = + + + 1 11 12 1 1 2 21 22 2 2 1 2 = n n m m m mn n y a a a x y a a a x y a a a x                   = =                         Y AX T m [ y , y , , y ] Y = 1 2  T n [x , x , , x ] X = 1 2 