
离散数学 课程教案 编号: 授课题目 5.4最短路径与关键路径 教学课型 理论课☑讨论课口实验课口 (1) 习题课口实践课口其它口 授课时间 月日 时 1 固定座位教室☑移动座位教室口 智慧型互动教室口 教学场所 实验(实训)室口校外实践基地口 户外口 其它口 教材简析: 本节内容为第五章第四节最短路径、关键路径与着色问题第一节课讲解,将图论知 识用于实际问题的解决,也是对所学知识综合掌握程度的一个检验,涉及到图的通路、 路径长度、边的赋权等知识,以及矩阵计算方法等,综合性较强,内容难度较大。但是 本节内容中最短路径算法是后续关键路径等问题解决的基础,有着十分重要意义,教学 过程中注重算法的介绍与应用,通过实例分析激发学生的探究欲望,实现教学大纲目标, 为下一步的学生打下坚实基础。 学情分析: 学生通过前段时间的学习,对图论相关理论知识已基本掌握,但对于图论的应用的 起源,应用的领域以及图论中涉及的算法还有许多未知,通过本节课内容学习,学生 方面可以对本课程学习的意义有更深的理解,同时对图论知识有一个概括和全面的认 知,对实际问题的解决有更多思路与方法。 当代大学生虽然心智比较成熟,但仍有部分大学生是比较自负和自私的,不懂得感 恩,人生观和价值观等有待更进一步的塑造,中国邮路问题是最短路径最具代表性的实 例,也是我们中国人在近代数学史上的骄傲,另外最短路径的求解和一带一路建设有- 个共同的本质,追求效益最大化,把握好契机,充分挖掘思政素材,开展合理的课程思 政,学生可以增强爱国主义情怀,体验一带一路精神,提升社会责任感和历史使命感。 考虑到少数计算机功底好的学生会尝试将算法在计算机软件中去实现,但在编码过 程中可能会遇到困难,为了帮助学生解决这些难题,可以将迪杰斯特拉算法的编码上传 到学习通平台,以供参考
离散数学 课程教案 编 号: 授 课 题 目 5.4 最短路径与关键路径 (1) 教学课型 理论课 讨论课□ 实验课□ 习题课□ 实践课□ 其 它□ 授课时间 月 日 学 时 1 教学场所 固定座位教室 移动座位教室□ 智慧型互动教室□ 实验(实训)室□ 校外实践基地□ 户外□ 其它□ 教材简析: 本节内容为第五章第四节-最短路径、关键路径与着色问题第一节课讲解,将图论知 识用于实际问题的解决,也是对所学知识综合掌握程度的一个检验,涉及到图的通路、 路径长度、边的赋权等知识,以及矩阵计算方法等,综合性较强,内容难度较大。但是 本节内容中最短路径算法是后续关键路径等问题解决的基础,有着十分重要意义,教学 过程中注重算法的介绍与应用,通过实例分析激发学生的探究欲望,实现教学大纲目标, 为下一步的学生打下坚实基础。 学情分析: 学生通过前段时间的学习,对图论相关理论知识已基本掌握,但对于图论的应用的 起源,应用的领域以及图论中涉及的算法还有许多未知,通过本节课内容学习,学生一 方面可以对本课程学习的意义有更深的理解,同时对图论知识有一个概括和全面的认 知,对实际问题的解决有更多思路与方法。 当代大学生虽然心智比较成熟,但仍有部分大学生是比较自负和自私的,不懂得感 恩,人生观和价值观等有待更进一步的塑造,中国邮路问题是最短路径最具代表性的实 例,也是我们中国人在近代数学史上的骄傲,另外最短路径的求解和一带一路建设有一 个共同的本质,追求效益最大化,把握好契机,充分挖掘思政素材,开展合理的课程思 政,学生可以增强爱国主义情怀,体验一带一路精神,提升社会责任感和历史使命感。 考虑到少数计算机功底好的学生会尝试将算法在计算机软件中去实现,但在编码过 程中可能会遇到困难,为了帮助学生解决这些难题,可以将迪杰斯特拉算法的编码上传 到学习通平台,以供参考

教学目标: 一、知识目标: 1、了解中国邮路问题,知道最短路径的起源与定义。 2、学习最短路径计算方法,利用迪杰斯特拉算法独立完成最短路径问题的求解。 3、理解最短路径算法迪杰斯特拉算法,能尝试利用计算机软件写出相应代码。 二、能力目标: 1、思考中国邮路问题的解决,提高探究能力。 2、利用迪杰斯特拉算法解决最短路径实际问题,增强知识应用能力和解决实际问题的 能力。 3、完成课堂练习,增强知识运用能力和合作学习能力。 三、情感与价值目标 1、学习最短路径的定义以及最短路径的实际应用领域,树立效益最大化意识,并学会 追求最高效益,有助于形成良好高效的职业素养。 2、学习迪杰斯特拉算法,运用该算法解决最短路径实际问题,加深对本课程学习意义 的理解。 3、了解中国邮路问题的命名来历,华为芯片事件,提高民族自豪感,增强爱国主义情 怀,塑造学生科技创新、科技自立、勇于探索的工匠精神。 4、拓展了解什么是中国一带一路,明确一带一路对中国乃至全世界的战略意义,体验 祖国的大国担当,提升民族危机意识与历史使命感,践行社会主义核心价值观。 教学重点、难点: 重点:理解迪杰斯特拉算法基本步骤,画出迭代过程表,找出最短路径。 难点:理解迪杰斯特拉算法迭代过程,尤其是如何确定永久标号。 课程思政: 1、课程思政素材 1)中国邮路问题百科知识;华为芯片事件资料: 2)视频资料:一带一路是什么? 3)官方文字资料:一带一路的战略意义,一带一路体现的精神。 2、课程思政切入点: 1、新课引入环节:最短路径经典案例中国邮路问题的解决历程,华为芯片事件
教学目标: 一、知识目标: 1、 了解中国邮路问题,知道最短路径的起源与定义。 2、 学习最短路径计算方法,利用迪杰斯特拉算法独立完成最短路径问题的求解。 3、 理解最短路径算法迪杰斯特拉算法,能尝试利用计算机软件写出相应代码。 二、能力目标: 1、 思考中国邮路问题的解决,提高探究能力。 2、 利用迪杰斯特拉算法解决最短路径实际问题,增强知识应用能力和解决实际问题的 能力。 3、 完成课堂练习,增强知识运用能力和合作学习能力。 三、情感与价值目标 1、学习最短路径的定义以及最短路径的实际应用领域,树立效益最大化意识,并学会 追求最高效益,有助于形成良好高效的职业素养。 2、学习迪杰斯特拉算法,运用该算法解决最短路径实际问题,加深对本课程学习意义 的理解。 3、了解中国邮路问题的命名来历,华为芯片事件,提高民族自豪感,增强爱国主义情 怀,塑造学生科技创新、科技自立、勇于探索的工匠精神。 4、拓展了解什么是中国一带一路,明确一带一路对中国乃至全世界的战略意义,体验 祖国的大国担当,提升民族危机意识与历史使命感,践行社会主义核心价值观。 教学重点、难点: 重点:理解迪杰斯特拉算法基本步骤,画出迭代过程表,找出最短路径。 难点:理解迪杰斯特拉算法迭代过程,尤其是如何确定永久标号。 课程思政: 1、课程思政素材: 1)中国邮路问题百科知识;华为芯片事件资料; 2)视频资料:一带一路是什么? 3)官方文字资料:一带一路的战略意义,一带一路体现的精神。 2、课程思政切入点: 1、新课引入环节:最短路径经典案例-中国邮路问题的解决历程,华为芯片事件
2、例题讲解环节:最短路径实际的应用。 3、课程思政目标 了解中国邮路问题的来由华为芯片事件,提高民族自豪感,增强爱国主义情怀,塑造学 生科技创新、科技自立、勇于探索的工匠精神 2)观看视频:一带一路是什么?感受中国的国际担当和“和平合作,开放包容,互学 互鉴,互利共赢”的丝路精神,践行社会主义核心价值观。 3)思考个人学习现状,树立努力完成好当下任务的决心与信心 4、课程思政实施思略: ②依托素材1),采取探 究,启发,讨论等方法, 实现思政目标1) ③依托素材2),采取讲授、 ①钻研教材 情感体验等方法,实现思政 洗定素材 思政素材 目标2) 确定目标 思政目标 方法选择 ④采取反思个人现状、行动 实践等方式,检验和巩固思 政效果,实现思政目标3) 教学方式和手段: 基于对教材内容的分析和学情的分析,在各教学环节中,紧靠教学内容,为实现教学目 标,充分发挥学生在学习中的主体地位,将采取以下教学方式和教学手段 教学方式:讲授、案例分析、启发、展示、探究,实践等方式相结合 教学手段:将现代化教学工具如手机,电脑,投影仪等,学习软件如学习通,微师等, 网络交流平台如QQ,微信等,传统教学工具如黑板,教材等紧密结合
2、例题讲解环节:最短路径实际的应用。 3、课程思政目标: 了解中国邮路问题的来由华为芯片事件,提高民族自豪感,增强爱国主义情怀,塑造学 生科技创新、科技自立、勇于探索的工匠精神。 2)观看视频:一带一路是什么?感受中国的国际担当和“和平合作,开放包容,互学 互鉴,互利共赢”的丝路精神,践行社会主义核心价值观。 3)思考个人学习现状,树立努力完成好当下任务的决心与信心。 4、课程思政实施思路: 教学方式和手段: 基于对教材内容的分析和学情的分析,在各教学环节中,紧靠教学内容,为实现教学目 标,充分发挥学生在学习中的主体地位,将采取以下教学方式和教学手段: 教学方式:讲授、案例分析、启发、展示、探究,实践等方式相结合。 教学手段:将现代化教学工具如手机,电脑,投影仪等,学习软件如学习通,微师等, 网络交流平台如 QQ,微信等,传统教学工具如黑板,教材等紧密结合。 ① 钻研教材 选定素材 确定目标 方法选择 ③依托素材 2),采取讲授、 情感体验等方法,实现思政 目标 2) 思政素材 思政目标 ②依托素材 1),采取探 究,启发,讨论等方法, 实现思政目标 1) ④采取反思个人现状、行动 实践等方式,检验和巩固思 政效果,实现思政目标 3)
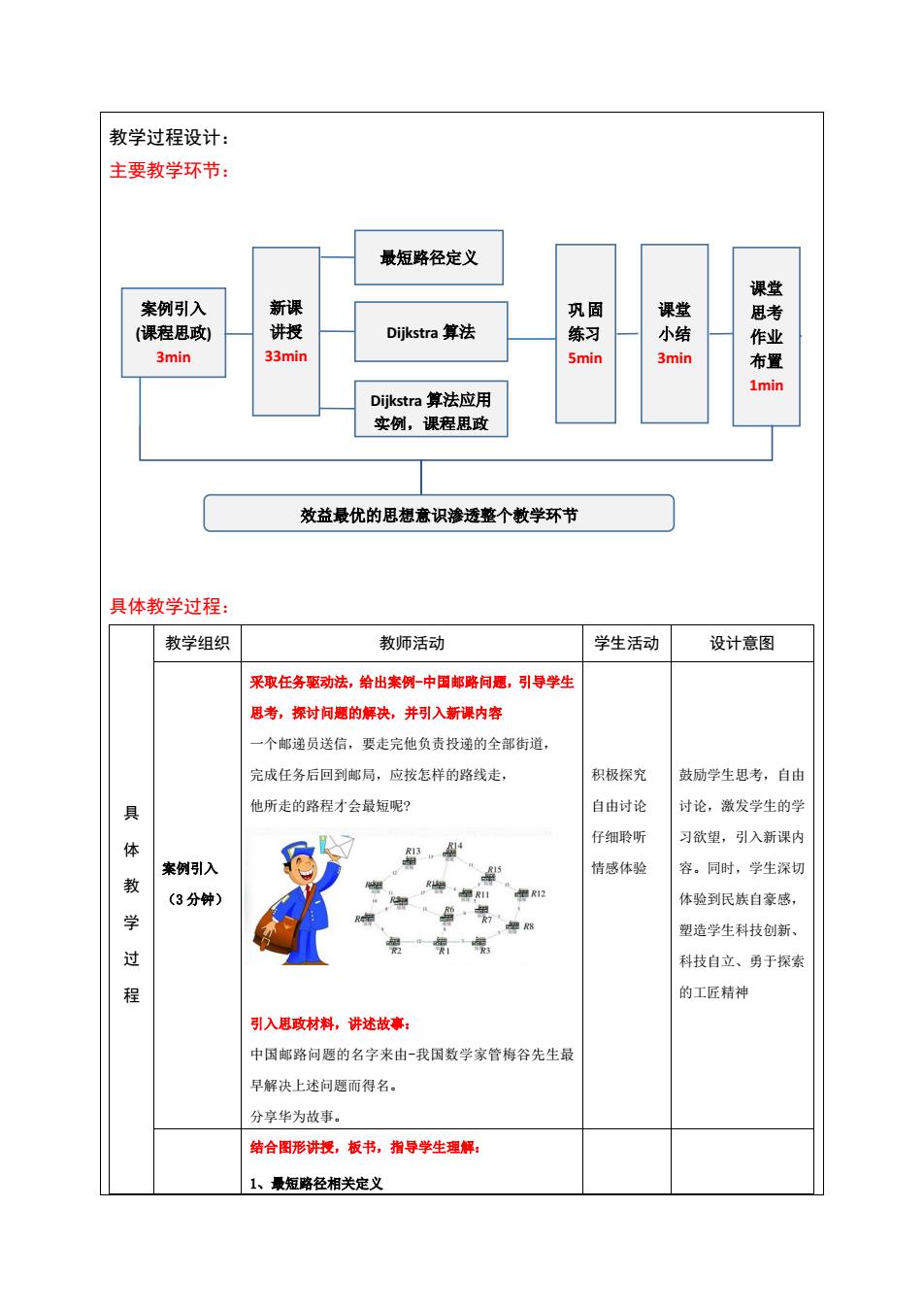
教学过程设计: 主要教学环节: 最短路径定义 案例引入 巩固 (课程思政] Dijkstra算法 练习 小 3min 33min i Dijkstra算法应用 实例,课程思政 效益最优的思想意识渗透整个教学环节 具体教学过程: 教学组织 教师活动 学生活动 设计意图 采取任务驱动法,给出素例-中国邮路愿,引导学生 思考,探时问摆的解决,并引入新溪内容 一个邮递员送信,要走完他负责投递的全部街道, 完成任务后回到邮局,应按怎样的路线走 积极探究 鼓励学生思考,自由 他所走的路程才会最短呢? 自由讨论 讨论,激发学生的学 体 仔细聆听 习欲,引入新课内 来例引入 情感体验 容,同时,学生深切 教 (3分钟) 体验到民族自豪感, 学 塑造学生科技创新、 过 科技自立、勇于探发 程 的工匠精神 引入思政材料,讲述故事: 中国邮路问题的名字来由一我国数学家管梅谷先生最 早解决上述问愿而得名。 分字华为故事。 结合图形洲授,板书,指导学生理解 1、承短略径相关定义
教学过程设计: 主要教学环节: 具体教学过程: 具 体 教 学 过 程 教学组织 教师活动 学生活动 设计意图 案例引入 (3 分钟) 采取任务驱动法,给出案例-中国邮路问题,引导学生 思考,探讨问题的解决,并引入新课内容 一个邮递员送信,要走完他负责投递的全部街道, 完成任务后回到邮局,应按怎样的路线走, 他所走的路程才会最短呢? 引入思政材料,讲述故事: 中国邮路问题的名字来由-我国数学家管梅谷先生最 早解决上述问题而得名。 分享华为故事。 积极探究 自由讨论 仔细聆听 情感体验 鼓励学生思考,自由 讨论,激发学生的学 习欲望,引入新课内 容。同时,学生深切 体验到民族自豪感, 塑造学生科技创新、 科技自立、勇于探索 的工匠精神 结合图形讲授,板书,指导学生理解: 1、最短路径相关定义 案例引入 (课程思政) 3min 新课 讲授 33min 最短路径定义 Dijkstra 算法 Dijkstra 算法应用 实例,课程思政 巩 固 练习 5min 课堂 小结 3min 课堂 思考 作业 布置 1min 效益最优的思想意识渗透整个教学环节

1.1定义1带权图G-,其中:E一R e∈E,oe称作e的权。 -作以.记ag若不相邻.记仙=0 12定义2设L是G中的一条路径,L的所有边的聆所 采用数形结合的方 权之和称作L的权记作。亿。 领悟 法,学生能更直观的 13定义3山和,之间的最烟路径山和v之间权最识记 学习和理解相关定义 小的通路。 如:右图 Li-Vs w(L/-10. L2-%影,oLJ-l2, 通过答愿情况可及时 Ly-vovwws.o(LjJ=11. 了解学生对最短路径 相关定义的掌握情 新授知识 设置拾答题 况,以便发现问题, (33分钟) 上图中,到各自顶点的最短路径的长度为多少?即求 解决问愿:设置抢答 解最短路径问题。 题环节,形成竞争机 课外任务布置:查找相关资料或者参考学习通平台误 思考 制,提高学生的专注 外资源。了解最短路问题的常用算法:Dijkstra算法, 抢答 力和反应能:通过 Bellman-Ford算法,Floyd算法和SPFA算法等,了解 课外任务的设置,拓 各种算法的适用情况。 展学生的知识而,提 高自主学习能力 针对本节难点与重点内容,先指导学生阅读教材,然 后师生合作复述的方式,将算法关步臻进行板书 2、迪杰斯特拉D时ksta算法(标号法)介绍 2.1算法记号说明: 迪杰斯特拉算法实质上一种标号法,每一个顶点有 个标号,分为永久性标号和临时标号两种
具 体 教 学 过 程 新授知识 (33 分钟) 1.1 定义 1 带权图 G=, 其中 ω:E→R, e E , ω(e)称作 e 的权。 e=(vi ,vj ), 记 ω(e)=wij . 若 vi ,vj不相邻, 记 ωij =∞。 1.2 定义 2 设 L 是 G 中的一条路径, L 的所有边的 权之和称作 L 的权,记作 ω(L)。 1.3 定义 3 u 和 v 之间的最短路径: u 和 v 之间权最 小的通路。 如:右图中 L1=v0v1v3v5 , ω(L1 )=10, L2=v0v1v4v5 , ω(L2 )=12, L3=v0v2v4v5 , ω(L3 )=11. 设置抢答题: 上图中 v1 到各自顶点的最短路径的长度为多少?即求 解最短路径问题。 课外任务布置:查找相关资料或者参考学习通平台课 外资源。了解最短路问题的常用算法:Dijkstra 算法, Bellman-Ford 算法,Floyd 算法和 SPFA 算法等,了解 各种算法的适用情况。 针对本节难点与重点内容,先指导学生阅读教材,然 后师生合作复述的方式,将算法关键步骤进行板书 2、迪杰斯特拉 Dijkstra 算法(标号法)介绍 2.1 算法记号说明: 迪杰斯特拉算法实质上一种标号法,每一个顶点有一 个标号,分为永久性标号和临时标号两种。 聆听 领悟 识记 思考 抢答 采用数形结合的方 法,学生能更直观的 学习和理解相关定义 通过答题情况可及时 了解学生对最短路径 相关定义的掌握情 况,以便发现问题, 解决问题;设置抢答 题环节,形成竞争机 制,提高学生的专注 力和反应能力;通过 课外任务的设置,拓 展学生的知识面,提 高自主学习能力

设带权图G=,其中e∈E,oe之0. =,2…。求,到其余各顶点的最短路径。 在顶点,的临时标号记做化户, 采取学生先自主阅读 在顶点,的永久标号记做P,广 自主学习 再复述的方式,鼓励 ,到的距离, 师生互动 学生在压力与动力并 Pn到的最短路径上的前一个项点, 认真聆听 存的学习氛围中,自 P已获得永久标号的集合, 积极思考 觉学习重点内容,提 T=V.P:仍为临时标号的集合. 仔细领会 高自主学习能力: 若,在第1步己获得永久标号,则此后它的标号不再 采取师生合作的方式 改变。 降低了学生的学习难 2.2具体算法过 度,提高学生的学习 年 设带权图G=,其中e∈E,oe之0. 信心、合作学习能力、 新授知识 0令 师生默契程度:对难 (33分钟) 4←0,n←元,←0,p,←元,j=2,3m 点内容进行板书,可 P=.T=V-}.k←lt←l. 过 以帮助学生对难点知 ②对所有的∈T且gy)∈E 识的关注和理解。 令1←min,l+ag 若1=+,则令l,←↓P,← ③)求{=min,y,e, 令P←PUy,T←T-,k←1 ④◆1←1+L 若1<n,则转(2)。 着说明注意事项: 对学生一些容易混涌 (山)左箭头相当于赋值,等号. 和难以把握的知识点 (②对于有向图,只需把无向边改成有向边即可。 领 进行着重说明,帮助 ()算法的第一步中给定达代初始值,以通路长 聆听 学生进一步理解难点 度达到最短为选代条件
具 体 教 学 过 程 新授知识 (33 分钟) 设带权图 G=, 其中 e E ,ω(e) 0。 V={v1 ,v2 ,...,vn}, 求 v1 到其余各顶点的最短路径。 在顶点 vi 的临时标号记做(li,, pi ), 在顶点 vi 的永久标号记做(li,, pi ) * , li:v1 到 vi的距离, pi:v1到 vi 的最短路径上 vi 的前一个顶点, P:已获得永久标号的集合, T=V-P:仍为临时标号的集合。 若 vi 在第 t 步已获得永久标号,则此后它的标号不再 改变。 2.2 具体算法过程 设带权图 G=, 其中 e E ,ω(e) 0。 (1) 令 1 1 1 1 0, , , , 2,3,... { }, { }, 1, 1. j j l p l p j n P v T V v k t , (2) 对所有的 j v T 且 ) k j (v v E , 令 min{ , }, j k kj l l l 若 , k kj l l 则令 , . j j k l l p v (3) 求 min{ | }, i j j l l v T 令 { }, { }, . P P v T T v k i i i (4) 令 t t 1, 若 t n ,则转(2)。 着重说明注意事项: (1) 左箭头相当于赋值,等号。 (2) 对于有向图,只需把无向边改成有向边即可。 (3) 算法的第一步中给定迭代初始值,以通路长 度达到最短为迭代条件。 自主学习 师生互动 认真聆听 积极思考 仔细领会 领悟 聆听 采取学生先自主阅读 再复述的方式,鼓励 学生在压力与动力并 存的学习氛围中,自 觉学习重点内容,提 高自主学习能力; 采取师生合作的方式 降低了学生的学习难 度,提高学生的学习 信心、合作学习能力、 师生默契程度;对难 点内容进行板书,可 以帮助学生对难点知 识的关注和理解。 对学生一些容易混淆 和难以把握的知识点 进行着重说明,帮助 学生进一步理解难点

(4)每一步都有一个顶点获得水久标号,都可以 内容:同时培养学生 获得起点到某个顶点的最短路径。若有”个顶点,需 有关主要矛盾和次要 要进行n步。 矛质的辩证唯物主义 所有选代步骤用过程表表示最直观。下述例中会有 观点 体现。 例举算法的应用实例,将所学知识学以致用 3、迪杰新特拉算法应用实例 例1如下带权无向图,求6到的最短路径。 具 将问愿分解,逐步设间,引导学生思考,养素解决间 通过完成例题解答。 体 愿的方法: 探究 强化所学知识,并实 教 新授知识 该问避可以用迪杰斯特拉算法解决吗?如果可以, 观察 现知识的学以致用: 学 (33分钟) 要迭代几步?如何来记录每一步选代结果? 互动 引入迭代表,创新问 过 引出新知选代过程表: 模仿 题的解决方法,提高 程 用过程表来表示每一步迭代过程。 练习 学生解决问题的能 利用上述图例,对选代过程表的面法做出示范 力:对选代过程表以 解:算法过程表如下表图所示。 示范的形式完成,给 学生自主学习做好榜 样,能达到举一反 的效果 线代生银泰 通过演示,通过师生互动,引导学生学会视察过程表 到的最短路径:%,d成, 通过指定学生完成练 习的方式,教师可以 进一步引导学生自己继续观来过程表,思考,并指定 思考 实现因材施教,个别 学生回答 练习 指导 请说出到其余顶点的最短路径,并说出最短距离。 通过完成例解答
具 体 教 学 过 程 新授知识 (33 分钟) (4)每一步都有一个顶点获得永久标号,都可以 获得起点到某个顶点的最短路径。若有 n 个顶点,需 要进行 n 步。 所有迭代步骤用过程表表示最直观。下述例题中会有 体现。 例举算法的应用实例,将所学知识学以致用 3、迪杰斯特拉算法应用实例 例 1 如下带权无向图,求 v0到 v5的最短路径。 将问题分解,逐步设问,引导学生思考,探索解决问 题的方法: 该问题可以用迪杰斯特拉算法解决吗?如果可以,需 要迭代几步?如何来记录每一步迭代结果? 引出新知-迭代过程表: 用过程表来表示每一步迭代过程。 利用上述图例,对迭代过程表的画法做出示范: 解:算法过程表如下表图所示。 通过演示,通过师生互动,引导学生学会观察过程表 v0 到 v5 的最短路径: v0 v1 v2 v3 v5 , d(v1 , v5 )=9 进一步引导学生自己继续观察过程表,思考,并指定 学生回答 请说出 v1 到其余顶点的最短路径,并说出最短距离。 探究 观察 互动 模仿 练习 思考 练习 内容;同时培养学生 有关主要矛盾和次要 矛盾的辩证唯物主义 观点 通过完成例题解答, 强化所学知识,并实 现知识的学以致用; 引入迭代表,创新问 题的解决方法,提高 学生解决问题的能 力;对迭代过程表以 示范的形式完成,给 学生自主学习做好榜 样,能达到举一反三 的效果 通过指定学生完成练 习的方式,教师可以 实现因材施教,个别 指导 通过完成例题解答
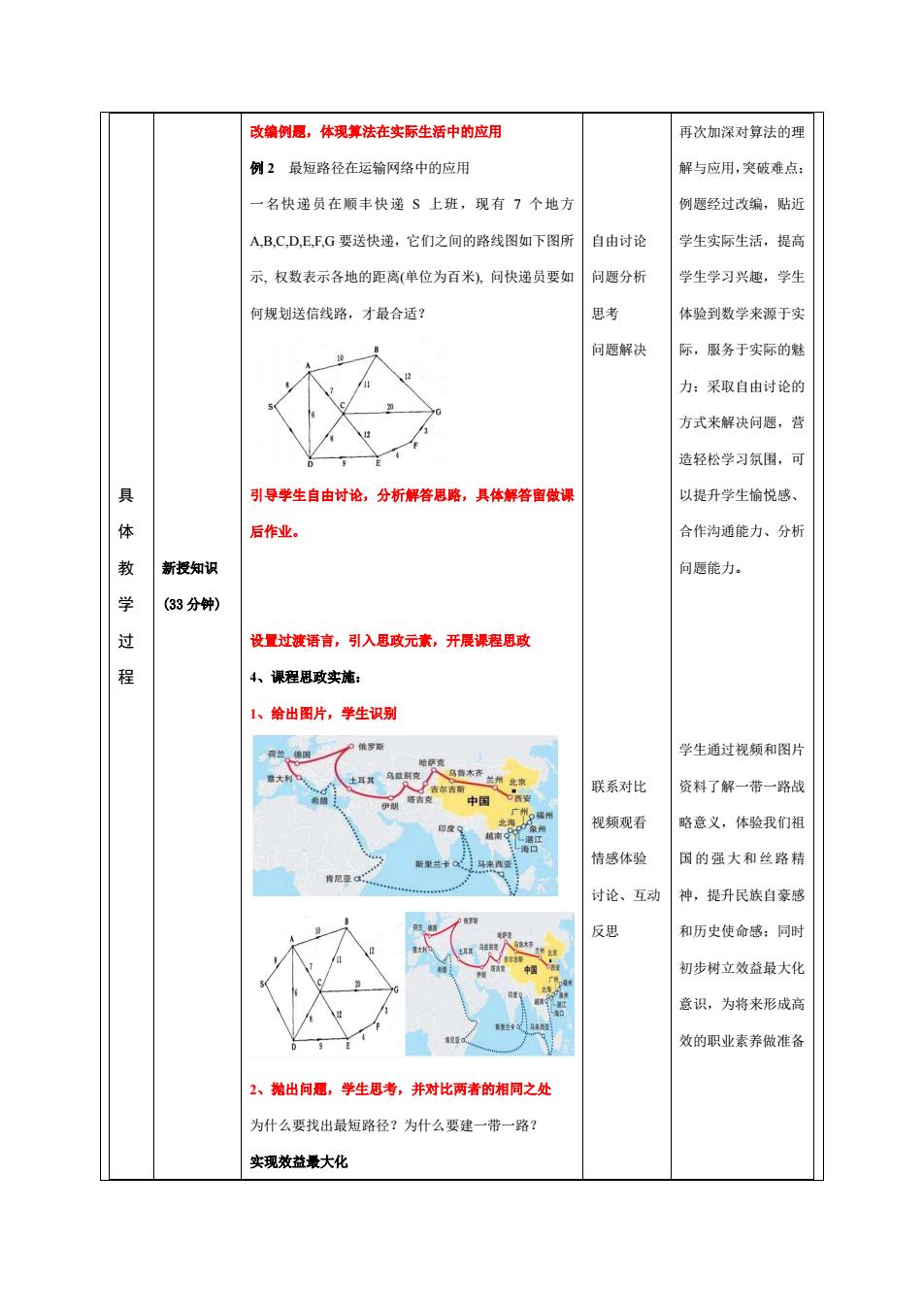
改编例愿,体现算法在实际生活中的应用 再次加深对算法的理 例2最短路径在运输网络中的应用 解与应用,突破难点: 一名快递员在顺丰快递S上班,现有7个地力 例题经过政编,贴近 AB,C,D,EFG要送快递,它们之间的路线图如下图所自由讨论 学生实际生活,提高 示,权数表示各地的距离(单位为百米),问快递员要如 问愿分析 学生学习兴趣,学生 何规划送信线路,才最合适? 体验到数学来源于实 问愿解决 际,服务于实际的魅 力:采取自由讨论的 方式来解决问题,营 造轻松学习氛用,可 引导学生自由讨论,分析解答思略,具体解答做 以提升学生榆悦感 后作业。 合作沟通能力、分析 新授知识 问题能力。 (33分钟) 慢置过液语言,引入思政元,开展课程思政 4、课程思政实施: 1、给出图片,擎生识别 学生通过视频和图片 联系对比 资料了解一带一路战 视频观看 略意义,体验我们祖 情感体验 国的强大和丝路精 讨论、互 神, 提升民族自豪感 反思 和历史使命感:同时 初步树立效益最大化 意识,为将来形成高 效的职业素养做准备 2、抛出问题,学生思考,并对比两者的相同之处 为什么要找出最短路径?为什么要建一带一路 实现效益最大化
具 体 教 学 过 程 新授知识 (33 分钟) 改编例题,体现算法在实际生活中的应用 例 2 最短路径在运输网络中的应用 一名快递员在顺丰快递 S 上班,现有 7 个地方 A,B,C,D,E,F,G 要送快递,它们之间的路线图如下图所 示, 权数表示各地的距离(单位为百米), 问快递员要如 何规划送信线路,才最合适? 引导学生自由讨论,分析解答思路,具体解答留做课 后作业。 设置过渡语言,引入思政元素,开展课程思政 4、课程思政实施: 1、给出图片,学生识别 2、抛出问题,学生思考,并对比两者的相同之处 为什么要找出最短路径?为什么要建一带一路? 实现效益最大化 自由讨论 问题分析 思考 问题解决 联系对比 视频观看 情感体验 讨论、互动 反思 再次加深对算法的理 解与应用,突破难点; 例题经过改编,贴近 学生实际生活,提高 学生学习兴趣,学生 体验到数学来源于实 际,服务于实际的魅 力;采取自由讨论的 方式来解决问题,营 造轻松学习氛围,可 以提升学生愉悦感、 合作沟通能力、分析 问题能力。 学生通过视频和图片 资料了解一带一路战 略意义,体验我们祖 国的强大和丝路精 神,提升民族自豪感 和历史使命感;同时 初步树立效益最大化 意识,为将来形成高 效的职业素养做准备
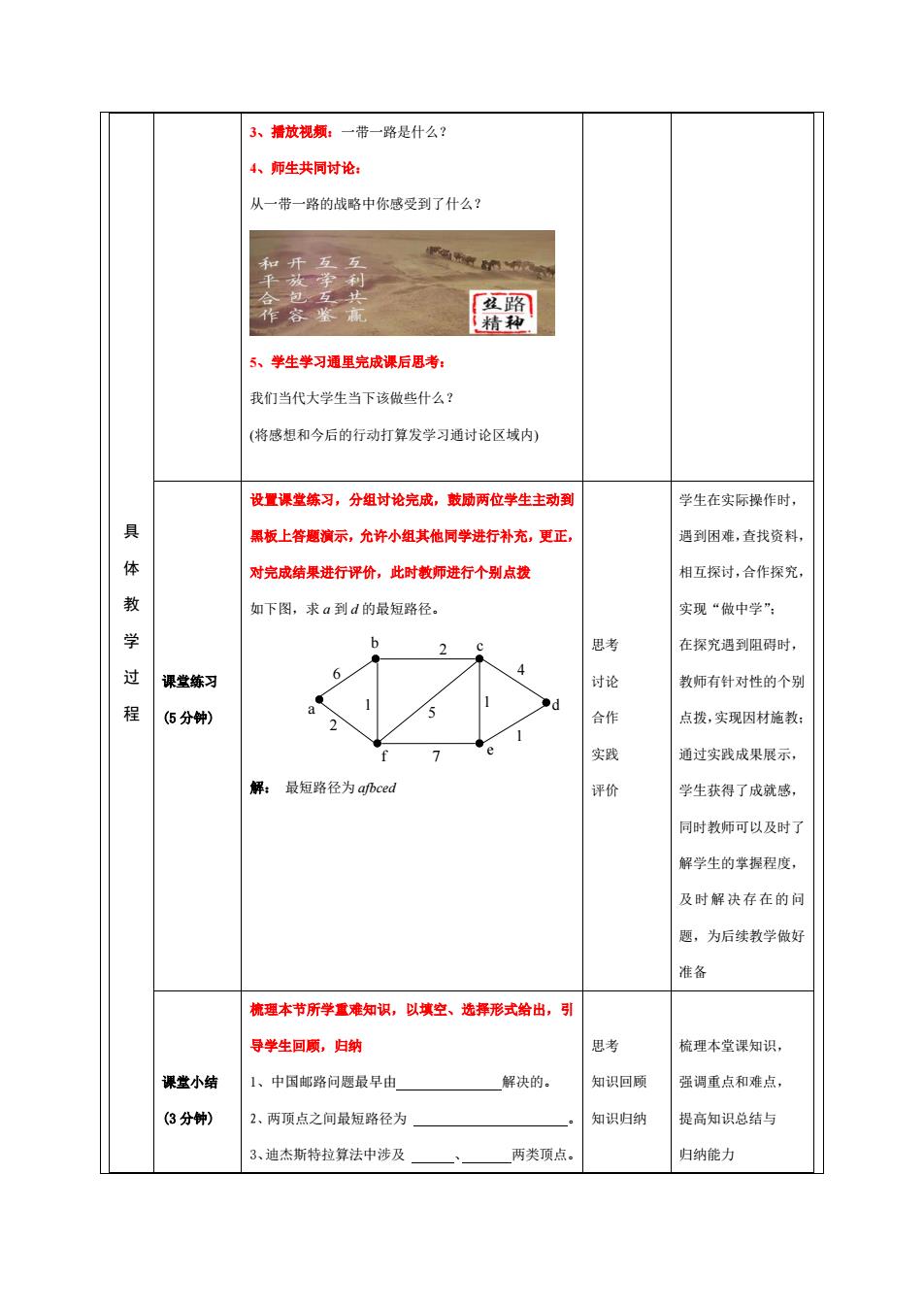
3、播放视颗:一带一路是什么? 4、师生共同讨论: 从一带一路的战略中你感受到了什么? 和南 「丝路 精种 5、学生学习通里完成课后思考: 我们当代大学生当下该做些什么? (格感想和今后的行动打算发学习通讨论区域内) 设置课堂练习,分组讨论完成,戴励两位学生主动到 学生在实际操作时, 具 黑板上答题演示,允许小组其他同学进行补充,更正, 通到困难,查找资料 体 对完成结果进行评价,此时教师进行个别点 相互探讨,合作探究 教 如下图,求a到d的最短路径。 实现“做中学” 学 思考 在探究遇到阻碍时, 过评堂练习 时e 教师有针对性的个别 程 (5分钟) 合作 点,实现因材施教 实成 通过实哦成果展示, 解:最短路径为afbced 学生获得了成就感。 同时教师可以及时了 解学生的掌提程度, 及时解决存在的问 题,为后续教学做 准备 梳理本节所学置难知识,以填空、选择形式给出,引 导学生回质,归钠 思考 梳理本堂课知识, 课堂小结 1、中国邮路问题最早由 解决的 知识回项 强调重点和难点, (3分钟) 2两项点之间最短路径为 知识归钠 提高知识总结与 3、迪杰斯特拉算法中涉及 两类项点。 归纳能力
具 体 教 学 过 程 3、播放视频:一带一路是什么? 4、师生共同讨论: 从一带一路的战略中你感受到了什么? 5、学生学习通里完成课后思考: 我们当代大学生当下该做些什么? (将感想和今后的行动打算发学习通讨论区域内) 课堂练习 (5 分钟) 设置课堂练习,分组讨论完成,鼓励两位学生主动到 黑板上答题演示,允许小组其他同学进行补充,更正, 对完成结果进行评价,此时教师进行个别点拨 如下图,求 a 到 d 的最短路径。 6 5 1 2 2 7 4 1 1 a b c d e f 解: 最短路径为 afbced 思考 讨论 合作 实践 评价 学生在实际操作时, 遇到困难,查找资料, 相互探讨,合作探究, 实现“做中学”; 在探究遇到阻碍时, 教师有针对性的个别 点拨,实现因材施教; 通过实践成果展示, 学生获得了成就感, 同时教师可以及时了 解学生的掌握程度, 及时解决存在的问 题,为后续教学做好 准备 课堂小结 (3 分钟) 梳理本节所学重难知识,以填空、选择形式给出,引 导学生回顾,归纳 1、中国邮路问题最早由 解决的。 2、两顶点之间最短路径为 。 3、迪杰斯特拉算法中涉及 、 两类顶点。 思考 知识回顾 知识归纳 梳理本堂课知识, 强调重点和难点, 提高知识总结与 归纳能力

4、”个顶点的最短路径算法过程表为一行列。 5、回亿迪杰斯特拉算法的选代过程。 1、复述并记录迪本斯特拉算法的具体步骤。 思考 巩固本节新知与思政 课后思考 2、课后作业:学习通平台作业5.4最短路径、关键归纳 效果,为下一节内容 作业布置 路径即着色问愿(1),例2. 练习 学习打好基础:提升 1分钟) 3、瘦看视频:观看学习通平台里“一带一路的意义”情感体验 学生课外阅读能力和 视频。 自主学习能力 4、预习:关键路径定义,网络图定义。 板书设计: 第1版 第2版 第3版活动板书: 标题 例题1的详细解答过 例题2步骤分析 迪杰斯特拉算法 程,即过程表板书 课堂练习解答 参考资料: 1、最短路径百科知识 https://baike.sogou.com/v168040147.htm?fromTitle=%E6%9C%80%E7%9F%AD%E8 %B7%AF%E5%BE%84%E7%AE%97%E6%B3%95 2、一带一路搜狗百科知识 https://baike.sogou.com/v76507736.htm?fromTitle=%E4%B8%80%E5%B8%A6%E4%B8%80 *E8%B7XAF 3、一带一路的意义 https://www.liuxue86.com/k %E4%B8%80%E5%B8%A6%E4%B8%80%E8%B7%AF%E7 %9A%84%E6%84%8F%E4%B9%891 4、课后复习参考教学视频及课件:学习通相关课程-章节5.4。 5、课后练习题参考答案:离散数学题解(第五版)[,耿素云主编,清华大学出版社 6、离散数学们,耿素云主编,北京大学出版社
4、n 个顶点的最短路径算法过程表为 行 列。 5、回忆迪杰斯特拉算法的迭代过程。 课后思考 作业布置 (1 分钟) 1、复述并记录:迪杰斯特拉算法的具体步骤。 2、课后作业:学习通平台作业 5.4 最短路径、关键 路径即着色问题(1),例 2。 3、观看视频:观看学习通平台里“一带一路的意义” 视频。 4、预习:关键路径定义,网络图定义。 思考 归纳 练习 情感体验 巩固本节新知与思政 效果,为下一节内容 学习打好基础;提升 学生课外阅读能力和 自主学习能力 板书设计: 参考资料: 1、最短路径百科知识 https://baike.sogou.com/v168040147.htm?fromTitle=%E6%9C%80%E7%9F%AD%E8 %B7%AF%E5%BE%84%E7%AE%97%E6%B3%95 2、一带一路搜狗百科知识 https://baike.sogou.com/v76507736.htm?fromTitle=%E4%B8%80%E5%B8%A6%E4%B8%80 %E8%B7%AF 3、一带一路的意义 https://www.liuxue86.com/k_%E4%B8%80%E5%B8%A6%E4%B8%80%E8%B7%AF%E7 %9A%84%E6%84%8F%E4%B9%89/ 4、课后复习参考教学视频及课件:学习通相关课程--章节 5.4。 5、课后练习题参考答案:离散数学题解(第五版)[M],耿素云主编,清华大学出版社。 6、离散数学[M],耿素云主编,北京大学出版社。 第 1 版 标题 迪杰斯特拉算法 第 2 版 例题 1 的详细解答过 程,即过程表板书 第 3 版 活动板书: 例题 2 步骤分析 课堂练习解答