
《离散数学》 第五章第四节 最短路径与关键路径 授课人王历容
《离散数学》 第五章第四节 最短路径与关键路径 授课人 王历容

5.4最短路径与关键路径 一、 最短路径相关定义 主要内容 二 ,、迪杰斯特拉算法 三、 迪杰斯特拉算法实例
5.4 最短路径与关键路径 一、 最短路径相关定义 二 、迪杰斯特拉算法 三 、迪杰斯特拉算法实例 主要内容

最短路径相关定义 新漫知识 2 迪太斯特拉算法 3 迪太斯特拉算法实例
新授知识 1 最短路径相关定义 3 迪杰斯特拉算法实例 2 迪杰斯特拉算法
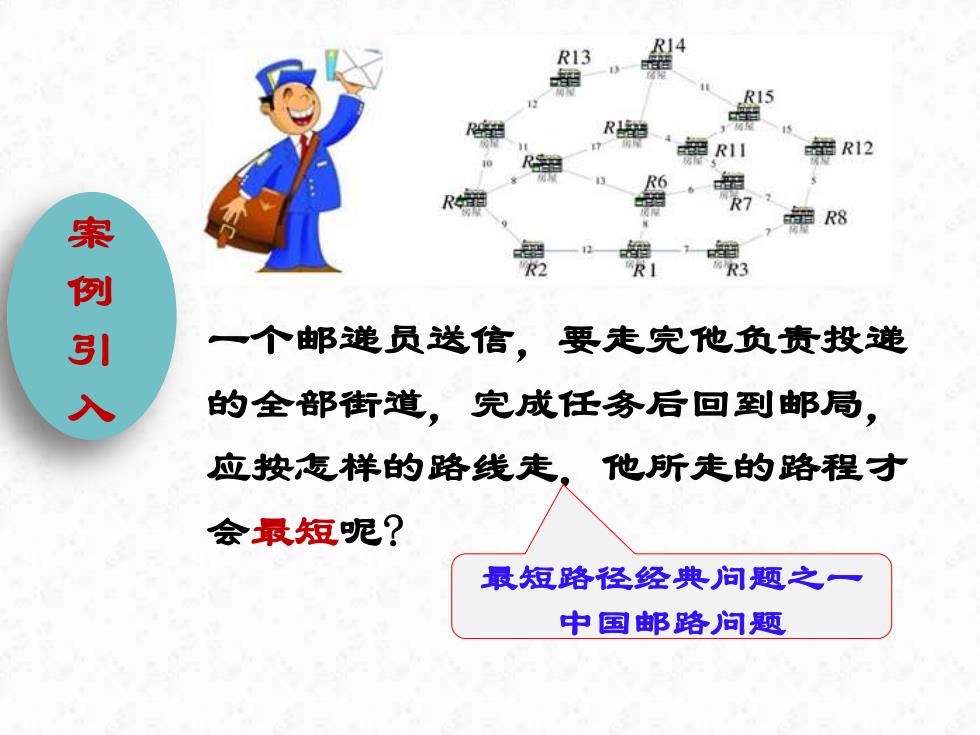
理R1 R12 都R8 案例引 R3 个邮递员送信,要走完他负责投递 的全部街道,完成任务后回到邮局, 应按怎样的路线走。他所走的路程才 会最短呢? 最短路径经典问题之一 中国邮路问题
一个邮递员送信,要走完他负责投递 的全部街道,完成任务后回到邮局, 应按怎样的路线走,他所走的路程才 会最短呢? 案 例 引 入 最短路径经典问题之一 中国邮路问题

创新精神、探索精神 名字来由:我国数学家管梅谷结合图论知识与 一笔画原理,在1962年最先解决了邮递员投递 路线问题,为国人争了光,于是在国际上称为 中国邮路问题
创新精神、探索精神 名字来由:我国数学家管梅谷结合图论知识与 一笔画原理,在1962年最先解决了邮递员投递 路线问题,为国人争了光,于是在国际上称为 中国邮路问题

HUAWEI

科技自立,时不我特 HUAWE 鸿蒙0S 我们不仅要坚持开放创新 更要实现科技自立 HA对I 5GCPE
我们不仅要坚持开放创新 更要实现科技自立 科技自立,时不我待
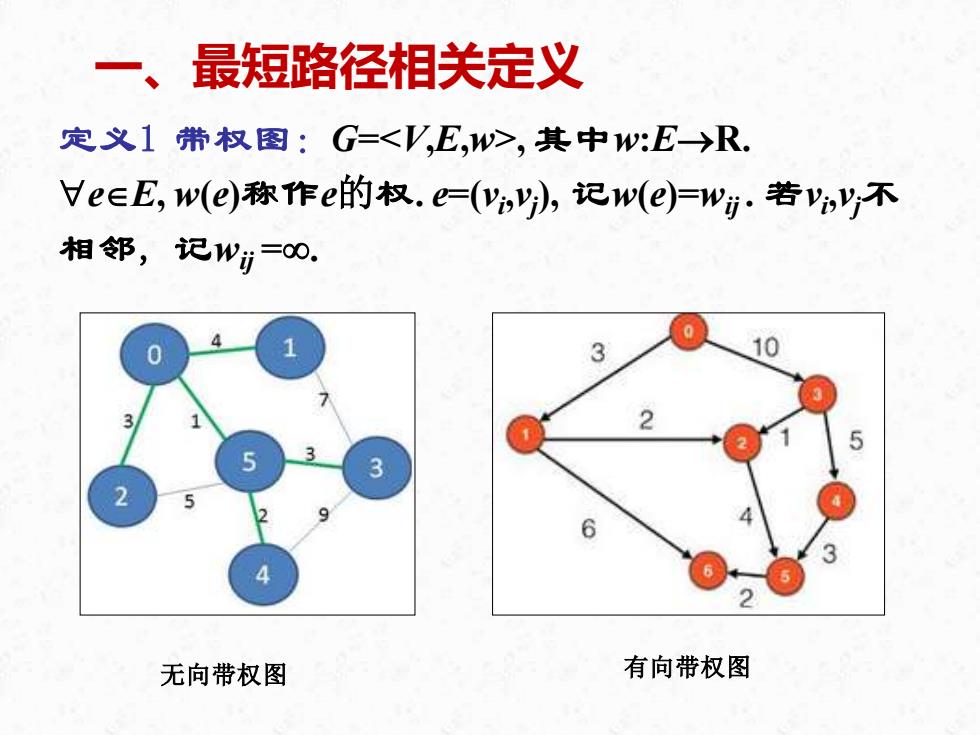
一、最短路径相关定义 定义1带权图:G=,其中w:E→R, Ve∈E,w(e)称作e的权.e=(y,记w(e)=w.若v不 相邻,记W=0. 3 10 无向带权图 有向带权图
一、最短路径相关定义 定义1 带权图:G=, 其中w:E→R. eE, w(e)称作e的权. e=(vi ,vj ), 记w(e)=wij . 若vi ,vj不 相邻, 记wij =. 无向带权图 有向带权图
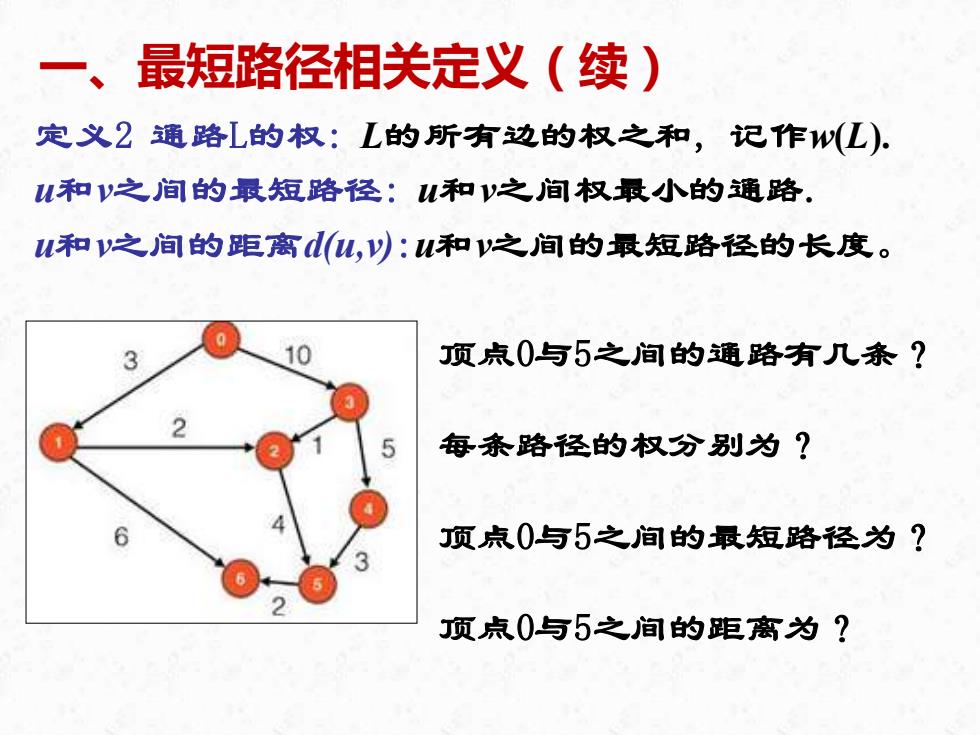
最短路径相关定义(续) 定义2通路L的权:L的所有边的权之和,记作w(L) 和v之间的最短路径:和y之间权最小的通路. u和v之间的距离d,y以:u和v之间的最短路径的长度。 3 10 顶点0与5之间的通路有几条? 5 每条路径的权分别为? 6 顶点0与5之间的最短路径为? 顶点0与5之间的距离为?
一、最短路径相关定义(续) 定义2 通路L的权: L的所有边的权之和, 记作w(L). u和v之间的最短路径: u和v之间权最小的通路. u和v之间的距离d(u,v):u和v之间的最短路径的长度。 顶点0与5之间的通路有几条? 每条路径的权分别为? 顶点0与5之间的最短路径为? 顶点0与5之间的距离为?
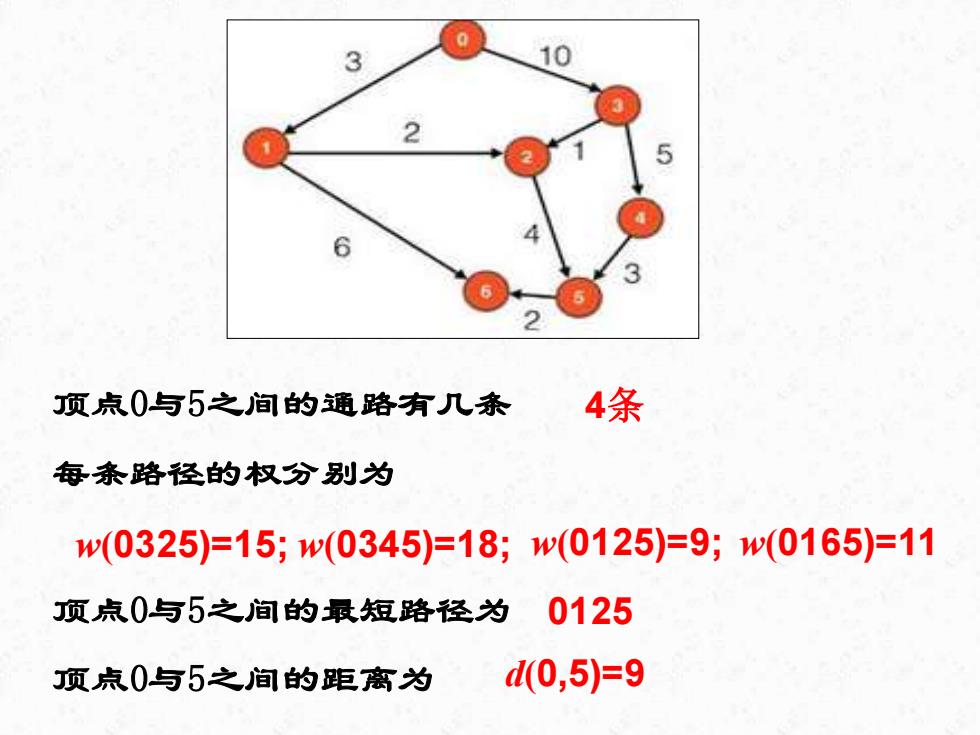
3 10 6 顶点0与5之间的通路有几条 4条 每条路径的权分别为 w(0325)=15;w(0345)=18;w(0125)=9;w(0165)=11 顶点0与5之间的最短路径为 0125 顶点0与5之间的距离为 d0,5)=9
顶点0与5之间的通路有几条 每条路径的权分别为 顶点0与5之间的最短路径为 顶点0与5之间的距离为 4条 w(0325)=15; w(0345)=18; w(0125)=9; w(0165)=11 0125 d(0,5)=9