
人红发手 《离散数学》 第六章第一节二部图 授课人王历容
《离散数学》 第六章 第一节 二部图 授课人 王历容

如何安排聪务? 班上四名同学竞选干部: 班长、团古出班长出习委员。竞 聘的区 人赵、小 钱、 支书,小 钱竞明 粤学习委 员、 员和团支 书。 女 能否使 得每付 真是伤脑筋呢
如何安排职务? 班上四名同学竞选干部: 班长、团支书、副班长、学习委员。竞 聘的四位候选者分别是小王、小赵、小 钱、小孙。小赵竞聘班长和团支书,小 钱竞聘班长和副班长,小孙竞聘学习委 员、副班长,小王竞聘学习委员和团支 书。如果四位同学都竞聘成功,能否使 得每位同学担任自己竞聘的职务?

6.1二部图(一) 二部图定义及判断 主要 内容 2 四配相关定义
6.1 二部图(一) 主要 内容 2 匹配相关定义 1 二部图定义及判断

1 二部图定义及判断 新授知识 2 匹配相关定义
新授知识 1 二部图定义及判断 2 匹配相关定义

一、二部图定义及判断 1、定义 二部图:无向图G=, 若将V划分成V1和V2 (VUV2=V,V∩V,=☑),使得G中的每条边的两个端点 一个属于V,另一个属于V2 记为G×V,V2,E>,称V和V2为互补顶点子集。 完全二部图:G是简单图,且V,中每个顶点都与 V,中每个顶点相邻,记为Ks,其中r=V1,5=V引 注意: n阶零图是二部图
一、二部图定义及判断 1、定义 二部图:无向图 G=, 若将V 划分成V1 和 V2 (V1V2 =V, V1V2 =), 使得G中的每条边的两个端点 一个属于V1 , 另一个属于V2。 记为G, 称V1和V2为互补顶点子集。 完全二部图: G是简单图, 且V1中每个顶点都与 V2中每个顶点相邻, 记为 Kr, s , 其中r =|V1 |, s=|V2 |。 注意: n 阶零图是二部图

分组讨论:判断下列图形是否为二部图 XXX 思考: 上述二部图具有什么共同特征?
分组讨论:判断下列图形是否为二部图 思考: 上述二部图具有什么共同特征?
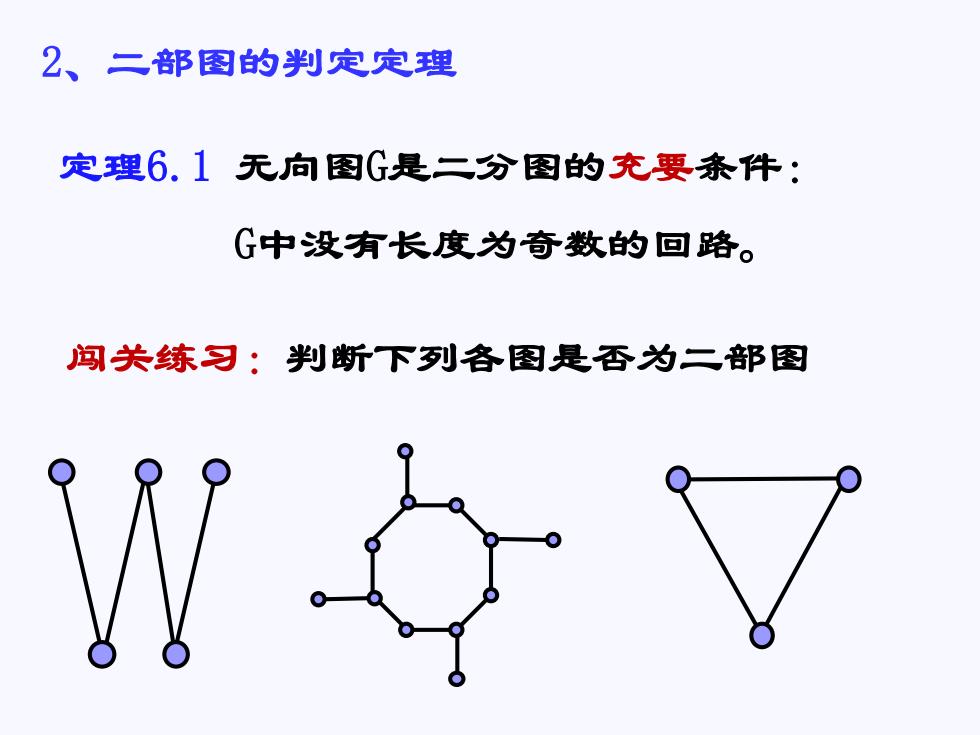
2、二部图的判定定理 定理6.1无向图G是二分图的充要条件: G中没有长度为奇数的回路。 闯关练习:判断下列各图是否为二部图
定理6.1 无向图G是二分图的充要条件: G中没有长度为奇数的回路。 2、二部图的判定定理 闯关练习:判断下列各图是否为二部图

没有回路的无向图是二部图吗? 推论6.1任何无回路的图均是二部图
推论6.1 任何无回路的图均是二部图。 没有回路的无向图是二部图吗?

二部图定义及判断 新授知识 2 四配相关定义
新授知识 1 二部图定义及判断 2 匹配相关定义

二、匹配相关定义 2定义1 设无向图G=,M三E 匹配(边独立集):M中任意2条边均不相邻的边子集; 极大匹配:添加任一条边后都不再是匹配; 最大匹配:边数最多的四配; 四配数:最大匹配中的边数, 记为B1·
二、匹配相关定义 2 定义1 设无向图 G= , M E 匹配(边独立集): M中任意2条边均不相邻的边子集; 极大匹配: 添加任一条边后都不再是匹配; 最大匹配: 边数最多的匹配; 匹配数: 最大匹配中的边数, 记为1 . a b c d