
真正讲透线性代数在二、三维空间的应用 ·工科线性代数现代化和大众化的思路之三 西安电子科技大学电子工程系陈怀琛 email:hchchen1934@vip.163.com 要:通过用线性代数对二三维向量空间进行分析和图解,使学生大大提高立体概念及其与线性变换 矩阵乘法及矩阵分解的关系。使得学习向量空间的概念更易接受并具有更强的实用性。 我在论文《论工科线性代数现代化和大众化》中曾经提出,对大学一年级的学生,能够 建立三维立体概念,己经是不低的要求了。其实教学计划中设立了好几门课程帮助达到这个 目的,如制图与画法几何,高等数学中的多变量微积分等,还有物理中的空间电磁场,数学 中的场论,电机课中的旋转磁场形成、乃至于信号处理中的复信号等等。线性代数也应该是 一个组成部分。我觉得至少对于弱电类的专业,实现的情况并不太好,学生的空间概念还是 很弱的,证据之一是许多学生,甚至部分毕业多年的教师,在后续课中,对频谱分析中的负 烦率,对信号处理中的复信号,都觉得难以理解。对机类专业而言,多自由度机器人,三坐 标测量仪,各种航行器在空间的运动,对线性代数在三维空间应用的要求更高。现有的线性 代数在此方面相当薄弱,很明显的 一点,就教材中使用的三维图形数目来比,中国教材往往 只有美国教材的10%以下,所以强化三维空间的概念是非常必要的。 一、 用二、三维向量来说明向量空间的运算规则 二维空间(平面)上的向量及其运算规则,特别是两个线性无关向量的线性组合是学生 理解线性代数的感性基础。MT的教材从下图讲向量的加减运算规则,进而列出其线性组 =[ +=[] 0 十十十 *-[+[]- -=-]-[8 图!向量的相加与相诚 合b=W+N=,再进一步的问题是平面上的任何向量b是否都能由这个线性组合 实现,其至设计了给定b猜测c,d的比赛,看谁能估计出最接近的c,d值。从这里又引入了 线性相关的概念,超定方程的概 (若b不在y平面上)等 从二维向量引深至三维向量和三维空间,并讨论向量的长度(范数)、向量的数量积(美 国的书上还喜欢用点乘(dot product)这个名词,MATLAB中也有点乘算符)、向量积和混合 积等。这时就有了更多的空间概念和图形。比如图2那样的图形
1 真正讲透线性代数在二、三维空间的应用 ——工科线性代数现代化和大众化的思路之三 西安电子科技大学电子工程系 陈怀琛 email: hchchen1934@vip.163.com 摘要:通过用线性代数对二三维向量空间进行分析和图解,使学生大大提高立体概念及其与线性变换、 矩阵乘法及矩阵分解的关系。使得学习向量空间的概念更易接受并具有更强的实用性。 我在论文《论工科线性代数现代化和大众化》中曾经提出,对大学一年级的学生,能够 建立三维立体概念,已经是不低的要求了。其实教学计划中设立了好几门课程帮助达到这个 目的,如制图与画法几何,高等数学中的多变量微积分等,还有物理中的空间电磁场,数学 中的场论,电机课中的旋转磁场形成、乃至于信号处理中的复信号等等。线性代数也应该是 一个组成部分。我觉得至少对于弱电类的专业,实现的情况并不太好,学生的空间概念还是 很弱的,证据之一是许多学生,甚至部分毕业多年的教师,在后续课中,对频谱分析中的负 频率,对信号处理中的复信号,都觉得难以理解。对机类专业而言,多自由度机器人,三坐 标测量仪,各种航行器在空间的运动,对线性代数在三维空间应用的要求更高。现有的线性 代数在此方面相当薄弱,很明显的一点,就教材中使用的三维图形数目来比,中国教材往往 只有美国教材的 10%以下,所以强化三维空间的概念是非常必要的。 一、 用二、三维向量来说明向量空间的运算规则 二维空间(平面)上的向量及其运算规则,特别是两个线性无关向量的线性组合是学生 理解线性代数的感性基础。MIT 的教材从下图讲向量的加减运算规则,进而列出其线性组 合 4 2 2 c d c d c d − + b v w = + = 。再进一步的问题是平面上的任何向量 b 是否都能由这个线性组合 实现,甚至设计了给定 b 猜测 c,d 的比赛,看谁能估计出最接近的 c,d 值。从这里又引入了 线性相关的概念,超定方程的概念(若 b 不在 xy 平面上)等。 从二维向量引深至三维向量和三维空间,并讨论向量的长度(范数)、向量的数量积(美 国的书上还喜欢用点乘(dot product)这个名词,MATLAB 中也有点乘算符)、向量积和混合 积等。这时就有了更多的空间概念和图形。比如图 2 那样的图形。 图 1 向量的相加与相减

而后在讲行列式的时候,又可以拿出图3的平行六面体说明三阶行列式的几何意义。 +,n+为.+ 图2三维空间的向量相加(左)和向量混合积(右) 人们都说线性代数是在几何与代数 之间建立的一座桥梁。所以把空间解析 几何放到线性代数中合并实施已经成为 许多学校的教学改革措施。几何是要用 图形说明概念的,线性代数既然作为桥 梁,必然要把图形,特别是三雏立体图 形放在特别重要的地位,把图形与代数 的表述与推导紧密结合,才能使学生理 (d1.a12.a13)← 解线性代数的方法论。线性代数的大众 化必须把这 点放在重要地位 而要做 到这一条,必须使对二三维向量空间的 图3三阶行列式等价于此平行六面体的体积 讨论在教材中占主要篇幅。如果突出N 维向量空间,那就必然扩大了公式推导的篇幅,图形就没有地位了! 用向量空间概念求超定方程组的好 用向量空间的方法往往可以更为简捷地推导公式,超定方程组的解可以作为一个例了 通常采用的是误差平方和最小的准则,其解也称为最小二乘解。国外所有作为公共课的线性 代数教材,都要讲这个内容,国内教材则几乎避开它。其实线性方程组只有适定、超定和欠 定三类,工程中要解决的只有前两类(因为欠 定方程属于条件不全的命题,工程师可以拒馅 12 解),不教学生解超定方程,等于浪费了线性 代数一半的功能。要严格地推导出最小二乘 的公式,利用空间几何概念是最方使而清楚 的。 在图1例中如果设b=5,10,求c,d,则可 4c-d=5 以得出以下的联立方程 2c+2ds10'解 c=2,d3。这是适定方程的情况其图形如右。 如果给出的是三维空间的b向量
2 而后在讲行列式的时候,又可以拿出图 3 的平行六面体说明三阶行列式的几何意义。 人们都说线性代数是在几何与代数 之间建立的一座桥梁。所以把空间解析 几何放到线性代数中合并实施已经成为 许多学校的教学改革措施。几何是要用 图形说明概念的,线性代数既然作为桥 梁,必然要把图形,特别是三维立体图 形放在特别重要的地位,把图形与代数 的表述与推导紧密结合,才能使学生理 解线性代数的方法论。线性代数的大众 化必须把这一点放在重要地位。而要做 到这一条,必须使对二三维向量空间的 讨论在教材中占主要篇幅。如果突出 N 维向量空间,那就必然扩大了公式推导的篇幅,图形就没有地位了! 二、 用向量空间概念求超定方程组的解 用向量空间的方法往往可以更为简捷地推导公式,超定方程组的解可以作为一个例子。 通常采用的是误差平方和最小的准则,其解也称为最小二乘解。国外所有作为公共课的线性 代数教材,都要讲这个内容,国内教材则几乎避开它。其实线性方程组只有适定、超定和欠 定三类,工程中要解决的只有前两类(因为欠 定方程属于条件不全的命题,工程师可以拒绝 解),不教学生解超定方程,等于浪费了线性 代数一半的功能。要严格地推导出最小二乘解 的公式,利用空间几何概念是最方便而清楚 的。 在图 1 例中如果设 b=[5;10],求 c,d,则可 以得出以下的联立方程: 4 5 2 2 10 c d c d − = + = ,解得 c=2,d=3。这是适定方程的情况其图形如右。 如 果 给 出 的 是 三 维 空 间 的 b 向 量 图 2 三维空间的向量相加(左)和向量混合积(右) 图 3 三阶行列式等价于此平行六面体的体积 0 5 10 -2 0 2 4 6 8 10 12 w 2w v 3v b=3w+2v
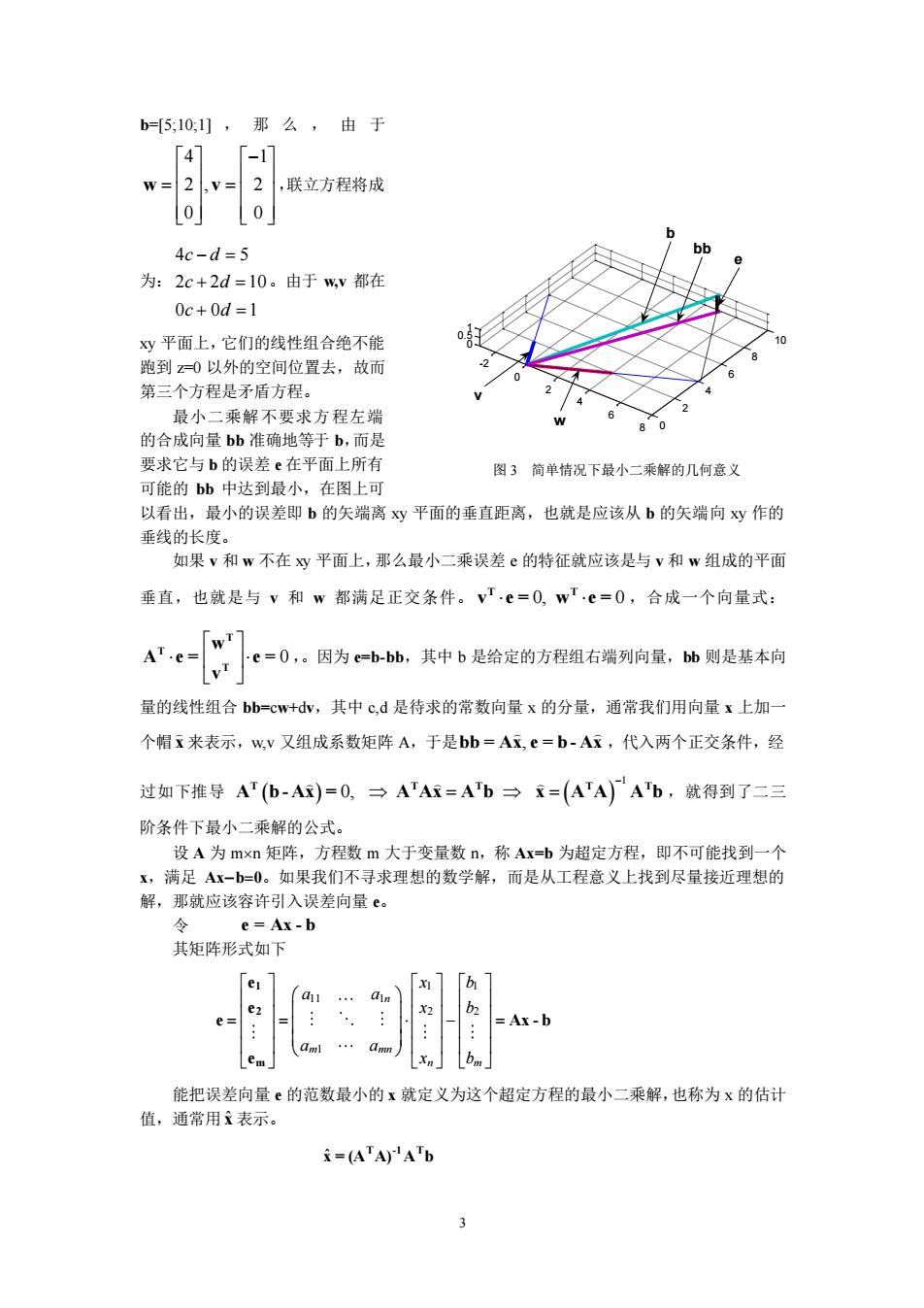
b=[5,101],那么,由于 「4「- w- 2v= 2 ,联立方程将成 00 4c-d=5 为:2c+2d=10。由于wv都在 0c+0d=1 y平面上,它们的线性组合绝不能 0.5 跑到0以外的空间位置去,故而 第三个方程是矛盾方程。 品木一垂解不要求方程左 2 0 的合成向量bb准确地等于 b,而是 要求它与b的误差e在平面上所有 图3简单情况下最小二乘解的几何意义 可能的bb中达到最小,在图上可 以看出,最小的误差即b的矢端离y平面的垂直距离,也就是应该从b的矢端向xy作的 垂线的长度。 如果v和w不在y平面上,那么最小二乘误差e的特征就应该是与v和w组成的平面 垂直,也就是与v和w都满足正交条件。ve=O,wIe=0,合成一个向量式: Are-fwi] =0,。因为e=b-bb,其中b是给定的方程组右端列向量,bb则是基本向 v 量的线性组合bb=cw+,其中c,d是待求的常数向量x的分量,通常我们用向量x上加 个帽x来表示,wv又组成系数矩阵A,于是bb=Ax,e-b-A,代入两个正交条件,经 过如下推导AT(b-A)=0,一ATAR=Ab一=(ATA)尸Ab,就得到了二三 阶条件下最小二乘解的公式。 设A为mxn矩阵,方程数m大于变量数n,称Ax=b为超定方程,即不可能找到一个 x,满足Ax-b=0。如果我们不寻求理想的数学解,而是从工程意义上找到尽量接近理想的 解,那就应该容许引入误差向量e。 e=Ax-b 其矩阵形式如下 能把误差向量的范数最小的x就定义为这个超定方程的最小二乘解,也称为×的估计 值,通常用立表示。 文=(ATA)ATb 3
3 b=[5;10;1] ,那么,由于 4 1 2 , 2 0 0 − = = w v ,联立方程将成 为: 4 5 2 2 10 0 0 1 c d c d c d − = + = + = 。由于 w,v 都在 xy 平面上,它们的线性组合绝不能 跑到 z=0 以外的空间位置去,故而 第三个方程是矛盾方程。 最小二乘解不要求方程左端 的合成向量 bb 准确地等于 b,而是 要求它与 b 的误差 e 在平面上所有 可能的 bb 中达到最小,在图上可 以看出,最小的误差即 b 的矢端离 xy 平面的垂直距离,也就是应该从 b 的矢端向 xy 作的 垂线的长度。 如果 v 和 w 不在 xy 平面上,那么最小二乘误差 e 的特征就应该是与 v 和 w 组成的平面 垂直,也就是与 v 和 w 都满足正交条件。 0, 0 T T v e = w e = ,合成一个向量式: 0 T T T w A e = e = v ,。因为 e=b-bb,其中 b 是给定的方程组右端列向量,bb 则是基本向 量的线性组合 bb=cw+dv,其中 c,d 是待求的常数向量 x 的分量,通常我们用向量 x 上加一 个帽 x 来表示,w,v 又组成系数矩阵 A,于是 bb = Ax e = b - Ax , ,代入两个正交条件,经 过如下推导 ( ) ( ) 1 0, − = = T T T T T A b - Ax = A Ax A b x A A A b ,就得到了二三 阶条件下最小二乘解的公式。 设 A 为 mn 矩阵,方程数 m 大于变量数 n,称 Ax=b 为超定方程,即不可能找到一个 x,满足 Ax−b=0。如果我们不寻求理想的数学解,而是从工程意义上找到尽量接近理想的 解,那就应该容许引入误差向量 e。 令 e = Ax - b 其矩阵形式如下 1 1 11 1 2 2 1 n m mn n m x b a a x b a a x b = = − = 1 2 m e e e Ax - b e 能把误差向量 e 的范数最小的 x 就定义为这个超定方程的最小二乘解,也称为 x 的估计 值,通常用 x ˆ 表示。 ˆ T -1 T x = (A A) A b -2 0 2 4 6 8 0 2 4 6 8 10 0 0.5 1 e v w b bb 图 3 简单情况下最小二乘解的几何意义

由于在推导过程中并未有任何一步对维数有过限制,这个公式在高维的线性代数方程中 同样适用。 在MAAB中,把运算(ATA)-IAT单独编成一个子程序,称为piv函数,它是 Psuedoinverse(伪逆或广义逆)的缩称。这样,求最小二乘解的公式可以写成:x=pinv(A)b, MATLAB把左除求解的符号x=Ab通用于适定、欠定和超定三种情况,系统会自动根据系 数矩阵A的维数n和m进行判断而得出适当的解,读者必须对这些解能作出正确的判读, 因此对于三种方程的解的特性要有清楚的概念 三、 QR分解及施密特正交系的几何意义 从下面的例题开始,先考虑二阶的问题。设两个列向量v1=(1:2),v2一(6:8),组成向量组: A-l=[16 ,作QR分解:A=QR= T-0.44720.89447[2.23614.4721 28 0.89440.4472 08.9443 在笛卡尔坐标系中画出列向量v1,v2如图3a,Q满足正交向量组的条件QQ=。它的两个 Q,1) Q:,2)是长度为 的单位向量 5 画出了它们的方向。R则是向量v1,v2在新坐 216.8 1 标系中的坐标值。它的第一列只有一个元素说 明新坐标系的第一根轴取的就是v1方向.第 根轴则按正交分解的要求取的是与v1 11,2) 方向。QR分解实际 上仅仅对 换,从原来的笛卡尔正交坐标系转到新的正交 坐标系。两者之间仅仅是转动了一个角度0, 图3a两维矩阵QR分解的几何意义 其实Q就是按0 cose -sine 与0关联的 gin月cosa 新坐标系的特点是其第一根轴沿着第一根向量,它不改变描述对象(此处是v山,2向量组) 的形状和大小。如果两个向量v1,v2调换一下位置,Q和日都会发生改变,因为这时新坐标 系的第一根轴将取为2的方向。 现在来看三维向量的情况,设三个列向量v1=(9-5,2,v2=0,7,5),v3(-1:-9,句,组成向量 组A:用MATLAB语句Q,R=qA)作QR分解后,得到: 0017 08581024750.4499 1048812383745766 0-826552.6727 0.1907065990.7267 094822 同样可以检验QQ=,说明Q是归一化的三维空间正交坐标系,R中第一个列向量只 有个元素,说明新坐标的第一根轴取的是v1方向:R中第二个列向量有两个元素,说明 新坐标的第二根轴是取在v1,v2平面上,方向与v1正交:它的 三个列向量有三个元素 说明它在新坐标系的 向都有分量。因为在立体图中画出三个列向量和 根新坐标轴不 太容易,画出来了也看不清楚,此处就不画了。 y 四、工程中需用QR分解的实例 点1 -0.28 -0.03 0.55 点2 4.04459 3.01 工程中很多情况都需要建立新的坐标系,绝大部 分是正交坐标系。各种航行器(飞机、汽车、船舶、 点30720.71 -0.13 航天器)都要有自己的机身坐标系。它们与地面笛卡 点42.72 42L 6.23 尔坐标系的关系通常用三个空间角(欧拉角)来度量 点51.97181-032
4 由于在推导过程中并未有任何一步对维数有过限制,这个公式在高维的线性代数方程中 同样适用。 在 MATLAB 中,把运算(ATA)−1AT 单独编成一个子程序,称为 pinv 函数,它是 Psuedoinverse(伪逆或广义逆)的缩称。这样,求最小二乘解的公式可以写成:x=pinv(A)* b, MATLAB 把左除求解的符号 x=A\b 通用于适定、欠定和超定三种情况,系统会自动根据系 数矩阵 A 的维数 n 和 m 进行判断而得出适当的解,读者必须对这些解能作出正确的判读, 因此对于三种方程的解的特性要有清楚的概念。 三、 QR 分解及施密特正交系的几何意义 从下面的例题开始,先考虑二阶的问题。设两个列向量 v1=(-1;2),v2=(6;8),组成向量组: 1 6 2 8 − = A = v , v 1 2 ,作 QR 分解: -0.4472 0.8944 2.2361 4.4721 0.8944 0.4472 0 8.9443 = A = QR 。 在笛卡尔坐标系中画出列向量 v1,v2 如图 3a,Q 满足正交向量组的条件 QTQ=I2。它的两个 列向量 Q(:,1)和 Q(:,2)是长度为 1 的单位向量, 它们代表了新建立的坐标系 x1 和 y1,在图中 画出了它们的方向。R 则是向量 v1,v2 在新坐 标系中的坐标值。它的第一列只有一个元素说 明新坐标系的第一根轴取的就是 v1 方向,第二 根轴则按正交分解的要求取的是与 v1 正交的 方向。QR 分解实际上仅仅是一个正交坐标变 换,从原来的笛卡尔正交坐标系转到新的正交 坐标系。两者之间仅仅是转动了一个角度 θ, 其实 Q 就是按 cos sin sin cos − = Q 与 θ 关联的: 新坐标系的特点是其第一根轴沿着第一根向量,它不改变描述对象(此处是 v1,v2 向量组) 的形状和大小。如果两个向量 v1,v2 调换一下位置,Q 和 θ 都会发生改变,因为这时新坐标 系的第一根轴将取为 v2 的方向。 现在来看三维向量的情况,设三个列向量 v1=(9;-5;2),v2=(0;7;5),v3=(-1;-9;6),组成向量 组 A:用 MATLAB 语句[Q,R]=qr(A)作 QR 分解后,得到: 9 0 -1 -0.8581 -0.2475 -0.4499 -10.4881 2.3837 -4.5766 -5 7 -9 , 0.4767 -0.7094 -0.5191 , 0 -8.2655 2 5 6 -0.1907 -0.6599 0.7267 = = = A Q R 2.6727 0 0 9.4822 同样可以检验 QTQ=I3,说明 Q 是归一化的三维空间正交坐标系,R 中第一个列向量只 有一个元素,说明新坐标的第一根轴取的是 v1 方向;R 中第二个列向量有两个元素,说明 新坐标的第二根轴是取在 v1,v2 平面上,方向与 v1 正交;它的第三个列向量有三个元素, 说明它在新坐标系的三个方向都有分量。因为在立体图中画出三个列向量和三根新坐标轴不 太容易,画出来了也看不清楚,此处就不画了。 四、 工程中需用 QR 分解的实例 工程中很多情况都需要建立新的坐标系,绝大部 分是正交坐标系。各种航行器(飞机、汽车、船舶、 航天器)都要有自己的机身坐标系。它们与地面笛卡 尔坐标系的关系通常用三个空间角(欧拉角)来度量, x y z 点 1 -0.28 -0.03 0.55 点 2 4.04 4.59 3.01 点 3 0.72 0.71 -0.13 点 4 2.72 4.21 6.23 点 5 1.97 1.81 -0.32 -10 -5 0 5 10 -10 -5 0 5 10 x 1 y1 v1(-1,2) v2(6,8) 图 3a 两维矩阵 QR 分解的几何意义

这三个欧拉角又可以换算为3×3的方向余弦矩阵,通常也都是正交矩阵。机器人或机械手 的每一个关节的运动参数多数都是角度,这类新坐标系是建立在实体对象上。所以新的正交 坐标系的变换矩阵应该把重点放在旋 不必太强调以数据为基础的QR分解) Q分解要求以数据点为基准来建立新坐标系,下面 个较好的例子:数控坐标测量 仪测出某气红截面上五个点的X,V,z坐标如右表:问这五点是近似在一个平面上吗?离平面 有多大误弟?试写出该诉似平面的数学方程: 解:根据工件和夹具的状况,被测平面与笛卡尔坐标系早任意空间关系,所以从测得的 一个平面上。最好是建立一个新坐标系,使它的 y坐标与这些点所 在这个坐标系中各 点的z坐标 就可反映它们对平面的误差 (I)把五个数据点坐标作为列向量组,建立数据矩阵A。它应是3×5矩阵。 028004040007200272001g700 A=-0.03004.59000.71004.21001.8100 0.55003.0100-0130062300-0.3200 2)这些点的共面性反映为它们的差向量是否共面,首先求出这五个点之间的差向量 把点5选为基准,令DA为差距咋,则DA=A-A(,5)*one(I,5),它也是3X5矩阵。它的第 五列全为零,是零向量或新坐标的原点。 -2.25002.0700.1.25000.7500 DA= -184002.7800-1.10002.4000 0.87003.33000.19006.5500 0 (B)对DA作QR变换Q,R=qr(DA),就相当 -0.7416-0.09190.664 [3.03402.26621.6486-0.1335 0 Q=-0.6065-0.33160.7227 R= 0-4.23870.3012-7.0148 0 02868-0.93890.1902 000.00040.00990 可见在新的坐标系内,五个点有三个的z坐标为零,即新坐标系的y平面由1,2, 点确定,其余两个点的z坐标值也都在0.01以下,说明这五个点基本共面。其三维立体 图如下。 11.22473.1796x+12.1093.1796-1 图(回五个空间测量点及其拟合平面b)坐标旋转后使拟合平面看似成为一根线
5 这三个欧拉角又可以换算为 3×3 的方向余弦矩阵,通常也都是正交矩阵。机器人或机械手 的每一个关节的运动参数多数都是角度,这类新坐标系是建立在实体对象上。所以新的正交 坐标系的变换矩阵应该把重点放在旋转角上,不必太强调以数据为基础的 QR 分解方法。 QR 分解要求以数据点为基准来建立新坐标系,下面是一个较好的例子:数控坐标测量 仪测出某气缸截面上五个点的 x,y,z 坐标如右表:问这五点是近似在一个平面上吗?离平面 有多大误差?试写出该近似平面的数学方程; 解:根据工件和夹具的状况,被测平面与笛卡尔坐标系呈任意空间关系,所以从测得的 数据无法看出它是否在一个平面上。最好是建立一个新坐标系,使它 的 xy 坐标与这些点所 在的平面大体重合,在这个坐标系中各点的 z 坐标,就可反映它们对平面的误差。 (1)把五个数据点坐标作为列向量组,建立数据矩阵 A。它应是 3×5 矩阵。 -0.2800 4.0400 0.7200 2.7200 1.9700 -0.0300 4.5900 0.7100 4.2100 1.8100 0.5500 3.0100 -0.1300 6.2300 -0.3200 = A (2)这些点的共面性反映为它们的差向量是否共面,首先求出这五个点之间的差向量, 把点 5 选为基准,令 DA 为差距咋,则 DA=A-A(:,5)*ones(1,5),它也是 3×5 矩阵。它的第 五列全为零,是零向量或新坐标的原点。 -2.2500 2.0700 -1.2500 0.7500 0 -1.8400 2.7800 -1.1000 2.4000 0 0.8700 3.3300 0.1900 6.5500 0 = DA (3)对 DA 作 QR 变换[Q,R]=qr(DA),就相当于 -0.7416 -0.0919 0.6645 3.0340 -2.2662 1.6486 -0.1335 0 -0.6065 -0.3316 -0.7227 , 0 -4.2387 0.3012 -7.0148 0 0.2868 -0.9389 0.1902 0 = = Q R 0 0.0004 0.0099 0 可见在新的坐标系内,五个点有三个的 z 坐标为零,即新坐标系的 xy 平面由 1,2,5 三点确定,其余两个点的 z 坐标值也都在 0.01 以下,说明这五个点基本共面。其三维立体 图如下。 图 (a) 五个空间测量点及其拟合平面 (b)坐标旋转后使拟合平面看似成为一根线

下面谈的几个问题在我们2005年及2007年的教材中已有体现,此处只列出几个标 趣和部分图形 五、向量在直线上的投影 设向量b-b,b,b,要求用矩阵乘法求它在z轴上和在xy坐标面上的投影。不难看 出,在z轴上的投影向量p为其x坐标b,而在y-z面上的投影向量Pz则是其在y,Z方向 投影b,b的向量和。用矩阵乘法来描写投影,可写出: [1001b, b. P=A,b=000 0 000b. 0 A和A,就是分别向x轴和y2平面上的投影矩阵。 设有另一个通过原点向量a=a,,Ⅱ,现在要求出b在a上的投影p 首先要在b的端点向a作垂 设它与a的延伸线相交于*a,w是一个数,p是投 影向量,D点也就是b到a的垂足。联线向量是向量b与D之差b-p,它应当与a正交,因 此两者的数乘积为零,即: (a,(b-w*a)》=a(b-e*a=0 a234 并求出w的值为: 42. 由p=w*a,知p=wa=aw= aab =Pb aa 其中P=a(aTa)'aT称为投影矩阵。求任何向量b 在向量a及其延伸直线上的投影,只要将该向量左 图4.5a向量b在向量a上的投影 乘投影矩阵P即可。 例4.2a设b2,2,1,a2,3,4T,求b在a方向的投影长度,并绘图说明。 解:在三维坐标内画出a,b向量如右,从b的矢端向向量a作垂线,与a交于p=v*? 点。用公式4,2a很容易求出w的值及p点坐标 4828.p产[0.9655,1.4483,1.9310 相应的MATLAB程序ea402a核心计算语句如下: a=2.3.4]'.b=2,2.1':w=a*b/a*a).p=w*a P=a*al(a*a)pl=P*b 程序云行结果为: v=0.4828 投影向量p=p1=[0.96551.4483 1.9310] [0.13790.20690.2759 投影矩阵P= 0.2069031030.4138 0.27590.41380.5517 各向量及其投影的图形可参阅图4.5a。ca402a中给出了详细的绘图程序,绘出图后还要 进行一定的图形编辑,才能得到此图中的箭头和文字。向量在直线上的投影公式是推导施密 特正交系构成公式的基础,但现在的绝大多数线性代数教材都不讲推理,而只把施密特正交 系的公式列出,让读者验证它们的正交性,所以避开了投影的公式,弄得许多线性代数老师 6
6 下面谈的几个问题在我们 2005 年及 2007 年的教材[2,3]中已有体现,此处只列出几个标 题和部分图形。 五、 向量在直线上的投影 设向量 b=[bx,by,bz] T,要求用矩阵乘法求它在 z 轴上和在 x-y 坐标面上的投影。不难看 出,在 z 轴上的投影向量 px 为其 x 坐标 bx,而在 y-z 面上的投影向量 pyz则是其在 y,z 方向 投影 by,bz的向量和。用矩阵乘法来描写投影,可写出: x yz 1 0 0 0 0 0 0 0 0 0 0 , 0 1 0 , 0 0 0 0 0 0 1 x x x y y y z z z b b b b b b b b b = = = = p = A b p = A b 1 2 A1 和 A2 就是分别向 x 轴和 yz 平面上的投影矩阵。 设有另一个通过原点向量 a=[ax,ay,az] T,现在要求出 b 在 a 上的投影 p 。 首先要在 b 的端点向 a 作垂线,设它与 a 的延伸线相交于 p=w*a,w 是一个数,p 是投 影向量,p 点也就是 b 到 a 的垂足。联线向量是向量 b 与 p 之差 b-p,它应当与 a 正交,因 此两者的数乘积为零,即: ,( ) ( ) 0 T a b- a a b- a w w = = 并求出 w 的值为: T T , , w = = a b a b a a a a 由 p=w*a,知 T w w T = = = = aa b p a a Pb a a 其中 ( ) 1 T T − P a a a a = 称为投影矩阵。求任何向量 b 在向量 a 及其延伸直线上的投影,只要将该向量左 乘投影矩阵 P 即可。 例 4.2a 设 b=[2,2,1] T,a=[2,3,4] T,求 b 在 a 方向的投影长度,并绘图说明。 解:在三维坐标内画出 a,b 向量如右,从 b 的矢端向向量 a 作垂线,与 a 交于 p=w*a 点。用公式(4.2a)很容易求出 w 的值及 p 点坐标: w=0.4828, p= [0.9655,1.4483,1.9310] T 相应的 MATLAB 程序 ea402a 核心计算语句如下: a=[2,3,4]'; b=[2,2,1]'; w=a'*b/(a'*a), p=w*a P=a*a'/(a'*a), p1=P*b 程序运行结果为: w = 0.4828 投影向量 p=p1 =[ 0.9655 1.4483 1.9310 ] T 投影矩阵 0.1379 0.2069 0.2759 0.2069 0.3103 0.4138 0.2759 0.4138 0.5517 = P 各向量及其投影的图形可参阅图 4.5a。ea402a 中给出了详细的绘图程序,绘出图后还要 进行一定的图形编辑,才能得到此图中的箭头和文字。向量在直线上的投影公式是推导施密 特正交系构成公式的基础,但现在的绝大多数线性代数教材都不讲推理,而只把施密特正交 系的公式列出,让读者验证它们的正交性,所以避开了投影的公式,弄得许多线性代数老师 图 4.5a 向量 b 在向量 a 上的投影

都不知道施密特是如何推导出他的公式的。 六、向量在平面上的投影 首先要在b的端点向a作垂线,设它与a的延伸线相交于点p,p是投影向量,P点也 就是b到a的垂足。它位于vL,v2张成的平面内,所以可写成它们的线性组合 p-水]小联是向量b与p之花p它应当与正交,因 与vl,v2两个向量的数乘积都为零,即: (y,(b-p》=v,b-A)=0l 三ATAx=Ab (b-p=v:'b-A)=0j 并求出x的值为: =(AAAb 由P=A,知p=A=A(A'A)Ab=Pb,其中P=A(ATA)AT ,求元p及P。 解A'A=11707 11 01212 35 012 0 ]-wm-B日-8-[] 「10 521 MATAB程序为: A=1,01,151,2b-[60,0 下面研究如何用投影矩阵方便地将立体图形投影到由a1,a2张成的倾斜平面上。设立体 图形为一个(长1宽15高2)的一笔画立方体C,它有8个顶点,原点及另一点经过两次, 故形成一个3×10的数据矩阵。 r00110001111 c=01.51.50001.51.500 0000022220 投影到al,a2张成的顿斜平面上的投影数据为D,则D-P*C,得到:
7 都不知道施密特是如何推导出他的公式的。 六、 向量在平面上的投影 设有两个通过原点的三维列向量 v1=[ax,ay,az] T,v2=[ax,ay,az] T,系数矩阵 A=[v1,v2] 为 3 ×2 维,张成了一个平面 a,现要求出向量 b 在 a 上的投影 p 。 首先要在 b 的端点向 a 作垂线,设它与 a 的延伸线相交于点 p,p 是投影向量,p 点也 就是 b 到 a 的垂足。它位于 v1,v2 张成的平面内,所以可写成它们的线性组合 1 2 = = 1 2 1 2 x p v , v v , v x x 联线向量是向量 b 与 p 之差 e=b-p,它应当与 a 正交,因此 与 v1,v2 两个向量的数乘积都为零,即: 2 2 ,( ) ( ) 0 ,( ) ( ) 0 = = = = = T 1 1 T T T v b - p v b - Ax A Ax A b v b - p v b - Ax 并求出 x 的值为: ( ) −1 = T T x A A A b 由 p=A x ,知 ( ) −1 = = T T p Ax = A A A A b Pb ,其中 ( ) −1 = T T P A A A A 例3 设 1 0 6 1 1 , 0 1 2 0 = = A b ,求 x p P , 及 。 解: 1 0 6 1 1 1 3 3 1 1 1 6 1 1 , 0 0 1 2 3 5 0 1 2 0 1 2 0 = = = = T T A A A b ( ) 1 1 1 2 3 3 6 5 3 6 5 1 3 5 0 3 3 0 3 6 − − − = = = = = − − T T x x A A A b x ( ) 1 1 0 5 2 1 1 1 5 3 1 1 1 1 1 2 2 2 6 6 3 3 0 1 2 1 2 1 2 5 − − = = = − − T T P A A A A MATAB 程序为: A=[1,0;1,1;1,2];b=[6;0;0] P=A*inv(A'*A)*A', 下面研究如何用投影矩阵方便地将立体图形投影到由 a1,a2 张成的倾斜平面上。设立体 图形为一个(长 1 宽 1.5 高 2)的一笔画立方体 C,它有 8 个顶点,原点及另一点经过两次, 故形成一个 3×10 的数据矩阵。 0 0 1 1 0 0 0 1 1 1 0 1.5 1.5 0 0 0 1.5 1.5 0 0 0 0 0 0 0 2 2 2 2 0 C = 投影到 a1,a2 张成的倾斜平面上的投影数据为 D,则 D=P*C,得到:

「00.51.33330.83330033330.16671.00.50.8333 D=00.50.83330.333300.66671.16671.51.00.3333 00.50.33330.166701.66672.1667201.5-0.1667 将向量al,a2,立体一笔画图形C及其投影D均画在同一张图的左右子图上.用MATLAB 的三维图形转动功能,读者可用用鼠标来旋转此图形。在转动过程中,可以使l,a2及D转 成一根直线,表明这几个图形是共面的,D是一个平面图形(投影),而立体图C则在任意 转动过程中保持它的三维形像。 照片 动画就是: 三维图形和图像转换到二维平面上,投影是转换的手段之一。 线性代数在这个领域也有它重要的应用。 将立体形C影到量La组成的平面上 立体圈形C韵设影D,它是一个平面圈无 0 .1-1 -1-1 图3将立体图形C投影到任意平面上形成平面图形D 下面是求投影矩阵的程序及它如何把立体图形转换为平面投影的演示程序cpla403b A=1.0:1.1:1.21b=6:0:01 =)*A' C=[0,0.0,01.501,1501,000.0,00.0,20,1.521,1.521,021,0.0 D-(P*C); plot3([0.A(1.1)1.10.A(2.1)1.10.A(3.1)1.'b'.linewidth'3).hold on plot3([0.A(1.2)1.[0.A(22)1.10.A(3.2)1.'m'.'linewidth'.3) plot3(C(1.).C(2.).C(3.).r.linewidth.3) plot3(D(1.).D(.).D3.).g.linewidth.3) axis([-1.2.-1,2.-1.3]).axisequal,gridon 参考文献 [1]Gilbert Strang.Introduction to Linear Algebra.4th Edition.Wilsley Canbridge Press.2009 [☒陈深英杰民,线性代数实践及MATLAB入门,北京,电子工业出版社,20O5年10月 陈深高液萍,杨 工程戳性代数(MATLAB版),北京,电子工业出版社,2007年7月 rAlgebra with Aplications. editionPrentice-0 [固怀深论工科线性代数的现代化与大众化,高等数学研究,第15卷,第2期,2012年3月 [同陈杯深高波萍,用主元连乘法定义行列式一工科线性代数大众化的思路之二,教有数学2013年年会
8 0 0.5 1.3333 0.8333 0 -0.3333 0.1667 1.0 0.5 0.8333 0 0.5 0.8333 0.3333 0 0.6667 1.1667 1.5 1.0 0.3333 0 0.5 0.3333 -0.1667 0 1.6 D = 667 2.1667 2.0 1.5 -0.1667 将向量a1,a2,立体一笔画图形C及其投影D均画在同一张图的左右子图上。用 MATLAB 的三维图形转动功能,读者可用用鼠标来旋转此图形。在转动过程中,可以使 a1,a2 及 D 转 成一根直线,表明这几个图形是共面的,D 是一个平面图形(投影),而立体图 C 则在任意 转动过程中保持它的三维形像。 电影、照片和动画就是把三维图形和图像转换到二维平面上,投影是转换的手段之一。 线性代数在这个领域也有它重要的应用。 下面是求投影矩阵的程序及它如何把立体图形转换为平面投影的演示程序 epla403b A=[1,0;1,1;1,2];b=[6;0;0] P=A*inv(A'*A)*A', C=[0,0,0;0,1.5,0;1,1.5,0;1,0,0;0,0,0;0,0,2;0,1.5,2;1,1.5,2;1,0,2;1,0,0]'; D=(P*C); plot3([0,A(1,1)],[0,A(2,1)],[0,A(3,1)],'b','linewidth',3),hold on plot3([0,A(1,2)],[0,A(2,2)],[0,A(3,2)],'m','linewidth',3) plot3(C(1,:),C(2,:),C(3,:),'r','linewidth',3) plot3(D(1,:),D(2,:),D(3,:),'g','linewidth',3) axis([-1,2,-1,2,-1,3]),axis equal, grid on 参考文献 [1] Gilbert Strang, Introduction to Linear Algebra, 4th Edition, Wilsley-Cambridge Press, 2009 [2] 陈怀琛,龚杰民,线性代数实践及 MATLAB 入门,北京,电子工业出版社,2005 年 10 月 [3] 陈怀琛,高淑萍,杨威,工程线性代数(MATLAB 版),北京,电子工业出版社,2007 年 7 月 [4] Bernard Kolman,Introductory Linear Algebra with Aplications,7th edition, Prentice-Hall,2001 [5] 陈怀琛,论工科线性代数的现代化与大众化,高等数学研究,第 15 卷,第 2 期,2012 年 3 月 [6] 陈怀琛,高淑萍,用主元连乘法定义行列式——工科线性代数大众化的思路之二,教育数学 2013 年年会 -1 0 1 2 -1 0 1 2 -1 0 1 2 3 将立体图形 C投影到向量 a1,a2组成的平面上 z y a2 a1 C 原点o -1 0 1 2 -1 0 1 2 -1 0 1 2 3 x 立体图形 C的投影 D,它是一个平面图形 y z a2 a1 原点o D 图 3 将立体图形 C 投影到任意平面上形成平面图形 D