
第三章 序列的两种傅立叶变换 1
1 第三章 序列的两种傅立叶变换

序列的两种傅立叶变换 ·3.1序列信号的周期性和频率 ·3.2离散时间傅立叶变换(DTFT) ·3.3离散系统的频率特性 ·3.4周期序列的频谱一离散傅立叶级数 ·3.5离散傅立叶变换(DFT) 。3.6 DFT的特性 ·3.7用DT计算线性卷积 2
2 序列的两种傅立叶变换 • 3.1 序列信号的周期性和频率 • 3.2 离散时间傅立叶变换(DTFT) • 3.3 离散系统的频率特性 • 3.4 周期序列的频谱—离散傅立叶级数 • 3.5 离散傅立叶变换(DFT) • 3.6 DFT的特性 • 3.7 用DFT计算线性卷积

3.1序列信号的周期性和频率 ·连续信号的周期性:满足 x(t)=x(t+mp) m=0,±1,±2,… 的连续信号称为周期信号。其中最小的非零P值 称为信号的周期。 ·离散序列的周期性:对于序列x(n),若对所有 的n满足 x(n)=x(n+N) 称为周期序列,满足此式的最小值称为序列的 周期。 3
3 3.1 序列信号的周期性和频率 • 连续信号的周期性:满足 的连续信号称为周期信号。其中最小的非零P值 称为信号的周期。 • 离散序列的周期性:对于序列x(n),若对所有 的n满足 称为周期序列,满足此式的最小值N称为序列的 周期。 x(t) = x(t + mP) m = 0, 1, 2, x(n) = x(n + N)

连续信号的正负频率 连续余弦信号的频率成分:化为指数形式 c0s21-长+e) 因此它由正负两个频率成分组成。其几何意义可 以从运行g即312演示程序看出。 对正弦信号 j-sinf=)k-ey) 也可作类似的分析。也由正负两个频率成分组成
4 连续信号的正负频率 连续余弦信号的频率成分:化为指数形式 因此它由正负两个频率成分组成。其几何意义可 以从运行fgp312演示程序看出。 对正弦信号 也可作类似的分析。也由正负两个频率成分组成。 ( ) j t j t t e e 0 0 2 1 cos 0 − = + ( ) j t j t j t e e 0 0 2 1 sin 0 − = −
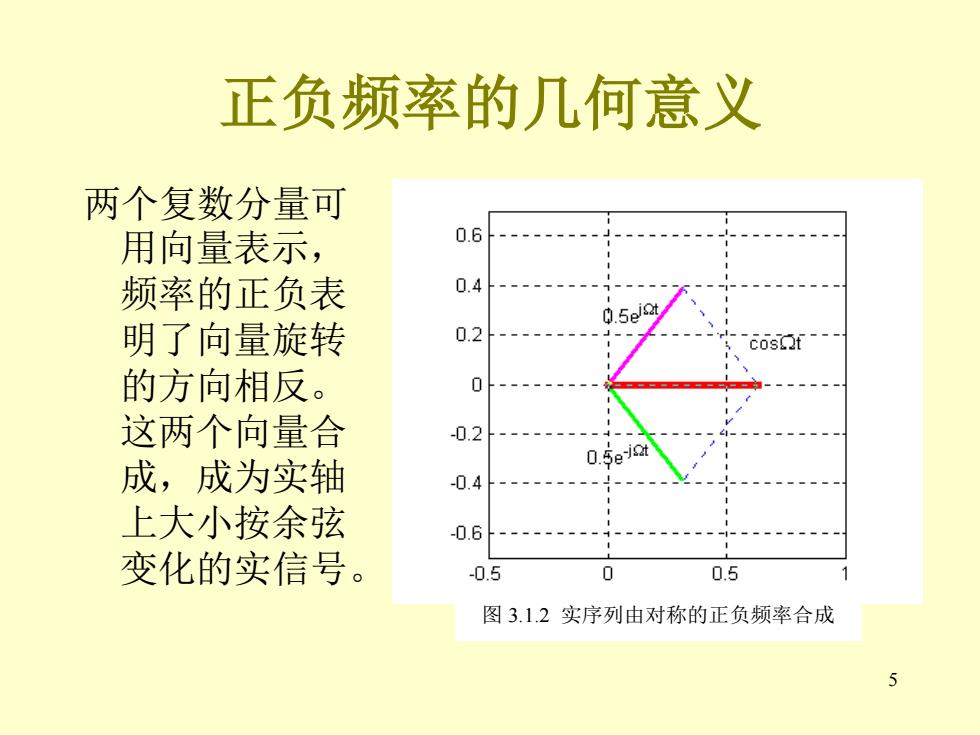
正负频率的几何意义 两个复数分量可 用向量表示, 0.6 频率的正负表 0.4 明了向量旋转 0.2 cos.t 的方向相反。 0 这两个向量合 -0.2 成,成为实轴 0.5e2t -04--------}-- 上大小按余弦 -0.6 变化的实信号。 -0.5 0 0.5 图3.1.2实序列由对称的正负频率合成 5
5 正负频率的几何意义 两个复数分量可 用向量表示, 频率的正负表 明了向量旋转 的方向相反。 这两个向量合 成,成为实轴 上大小按余弦 变化的实信号。 图 3.1.2 实序列由对称的正负频率合成

序列信号的周期性和频率 正弦连续信号sin2ot的频率fHz]是周期的倒数 20=2πf0=2π/P, 上述信号以=1/Fs采样的序列周期性条件为: x(n)=sinonT=sin(n+N)T 展开后得知,只有在满足: 20T=(2k/W)m 或foF、=foT=kN(k和N均为整数)的情况下, 才是周期序列。 6
6 序列信号的周期性和频率 正弦连续信号sinΩ0t的频率f0 [Hz]是周期的倒数 上述信号以T=1/Fs采样的序列周期性条件为: 展开后得知,只有在满足: 或f0 /Fs= f0T= k/N (k和N均为整数)的情况下, 才是周期序列。 2 2 / , 0 = f 0 = P 0 T = (2k / N) 0 0 x n nT n N T ( ) sin sin ( ) = = +

序列信号的周期性和频率 例如,设2T=0.1元,可求得N=2kπ/0.1π=20k,N 的最小值出现在k=1时,即N=20。 若把2增大三倍,设2T=0.3π,可求得 N=2kπ/0.3π=20k/3,N的最小整数值出现在 k=3时,仍有N=20. 两种情况的周期相同,但其序列包络的形状显 然不同,下图的频率为上图的三倍。因此不 能用周期的倒数来定义序列信号的频率。应 该用序列信号的包络(它是连续信号)频率 判断它所携带的频谱。 1
7 序列信号的周期性和频率 例如,设Ω0T=0.1π,可求得N=2kπ/0.1π=20k,N 的最小值出现在k=1时,即N=20。 若把Ω0增大三倍,设Ω0T=0.3π,可求得 N=2kπ/0.3π=20k/3,N的最小整数值出现在 k=3时,仍有N=20。 两种情况的周期相同,但其序列包络的形状显 然不同,下图的频率为上图的三倍。因此不 能用周期的倒数来定义序列信号的频率。应 该用序列信号的包络(它是连续信号)频率 判断它所携带的频谱
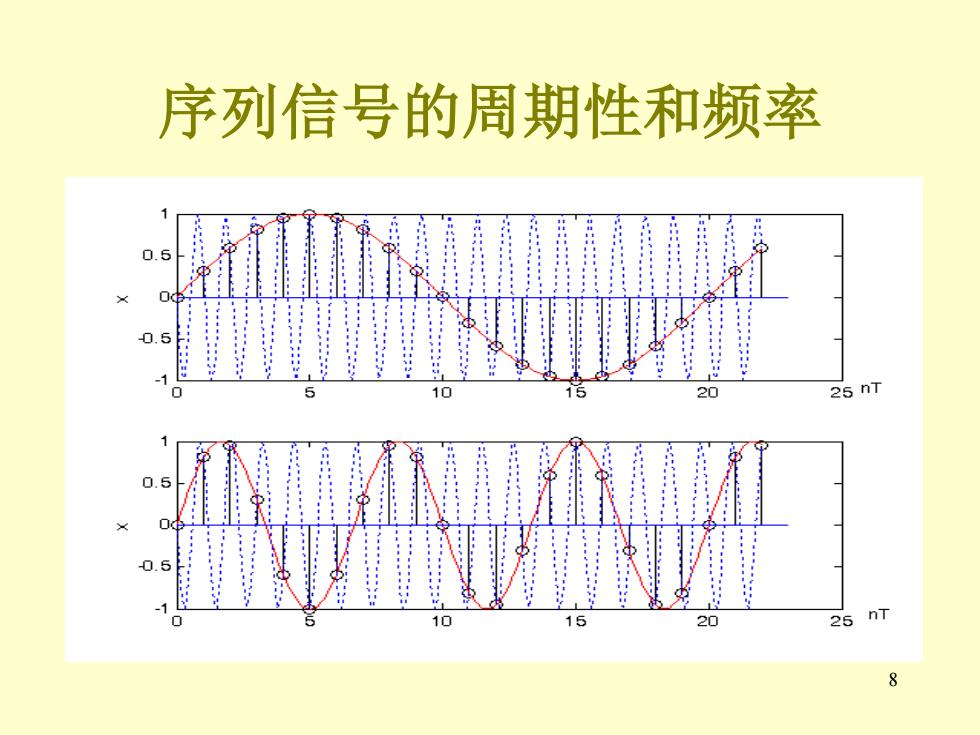
序列信号的周期性和频率 1 5 10 15 20 25 nT : -1 10 15 2 25 nT
8 序列信号的周期性和频率

序列信号的频率 序列的包络不是唯一的。在上面的图中,虚线的 波形也通过所有采样点,所以也是包络。它的 频率与红线所示包络的频率相差正好为Fs. 如果2是一个序列的包络频率,则 21=20 +2πk=20+2πkF,k=0,1, T 也是它的包络频率。所以一个连续正弦信号被采 样后,得到的离散序列将包含无数个数字频率。 9
9 序列信号的频率 序列的包络不是唯一的。在上面的图中,虚线的 波形也通过所有采样点,所以也是包络。它的 频率与红线所示包络的频率相差正好为Fs. 如果Ω0是一个序列的包络频率,则 也是它的包络频率。所以一个连续正弦信号被采 样后,得到的离散序列将包含无数个数字频率。 2 ( 0, 1, ) 2 1 = 0 + = 0 + k F k = T k s
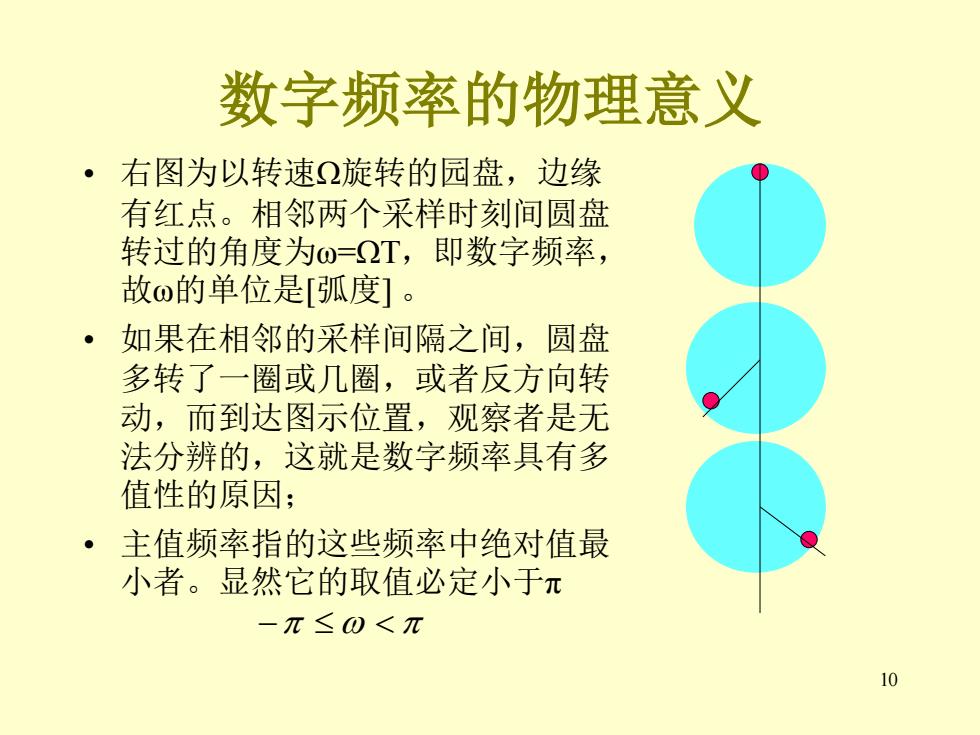
数字频率的物理意义 ·右图为以转速Ω旋转的园盘,边缘 有红点。相邻两个采样时刻间圆盘 转过的角度为ω=2T,即数字频率, 故o的单位是[弧度]。 ·如果在相邻的采样间隔之间,圆盘 多转了一圈或几圈,或者反方向转 动,而到达图示位置,观察者是无 法分辨的,这就是数字频率具有多 值性的原因; ·主值频率指的这些频率中绝对值最 小者。显然它的取值必定小于π -π≤0<元 10
10 数字频率的物理意义 • 右图为以转速Ω旋转的园盘,边缘 有红点。相邻两个采样时刻间圆盘 转过的角度为ω=ΩT,即数字频率, 故ω的单位是[弧度] 。 • 如果在相邻的采样间隔之间,圆盘 多转了一圈或几圈,或者反方向转 动,而到达图示位置,观察者是无 法分辨的,这就是数字频率具有多 值性的原因; • 主值频率指的这些频率中绝对值最 小者。显然它的取值必定小于π −