
5.2节 解析几何和多变量函数
5.2节 解析几何和多变量函数

5.2节 解析几何和多变量分析 0 本节主要讨论用MATLAB解决空间解析几何 的问题。重点是利用MATLAB的三维作图功 能,对多变量函数的性质进行更为形象的 讨论。 ·读者要从中学会曲面的绘制方法,等高线 图和方向导数(梯度)的计算和绘制,进 一步把它们的几何意义与解析表示式联系 起来
5.2节 解析几何和多变量分析 • 本节主要讨论用MATLAB解决空间解析几何 的问题。重点是利用MATLAB的三维作图功 能,对多变量函数的性质进行更为形象的 讨论。 • 读者要从中学会曲面的绘制方法,等高线 图和方向导数(梯度)的计算和绘制,进 一步把它们的几何意义与解析表示式联系 起来

极坐标系中的绘图 【例5-2-1】绘制极坐标系下的平面曲线 p=acos(b+ne) 并讨论参数a、b、n的影响。 ·◆建模绘图的基本方法仍然是先设置自变量数 组,按元数群运算的要求列出函数表示式,使得 一个表示式能够同时计算出与自变量数目相等的 因变量,立即可用来绘图。为了便于比较,编一 个能分别画出两个图形的程序,采用fo循环,读 者可从中看到利用循环指数的技巧。 ·由于有两种参数下的数据,因变量也有两组数据, 所以ho要设成二维的数组
极坐标系中的绘图 【例5-2-1】 绘制极坐标系下的平面曲线 并讨论参数a、b、n的影响。 • ◆建模 绘图的基本方法仍然是先设置自变量数 组,按元数群运算的要求列出函数表示式,使得 一个表示式能够同时计算出与自变量数目相等的 因变量,立即可用来绘图。为了便于比较,编一 个能分别画出两个图形的程序,采用for循环,读 者可从中看到利用循环指数的技巧。 • 由于有两种参数下的数据,因变量也有两组数据, 所以rho要设成二维的数组。 = + a b n cos( )

极坐标绘图程序exn521 theta=0:0.1:2*pi;%产生自变量(极角)向量 %或用theta=:linspace(0,2*pi,N); for i=1:2 a(0=input('a=(书上值为a(1)=2;a(2)=2); b(0=input('b=(书上值为b(1)=pil4;b(2)=0)): n(0=input('n=(书上值为n(1)=2;n(2)=3) rho(i,:)=a()*cos(b()+n()*theta);%因变量方程 subplot(1,2,i),polar(theta,rho(i,:);%绘图 end
极坐标绘图程序exn521 theta=0:0.1:2*pi; % 产生自变量(极角)向量 % 或用 theta=linspace(0,2*pi,N); for i=1:2 a(i)=input('a= (书上值为a(1)=2;a(2)=2)'); b(i)=input('b= (书上值为b(1)=pi/4;b(2)=0)'); n(i)=input('n= (书上值为n(1)=2;n(2)=3)') rho(i,:)=a(i)*cos(b(i)+n(i)*theta); %因变量方程 subplot(1,2,i),polar(theta,rho(i,:)); %绘图 end
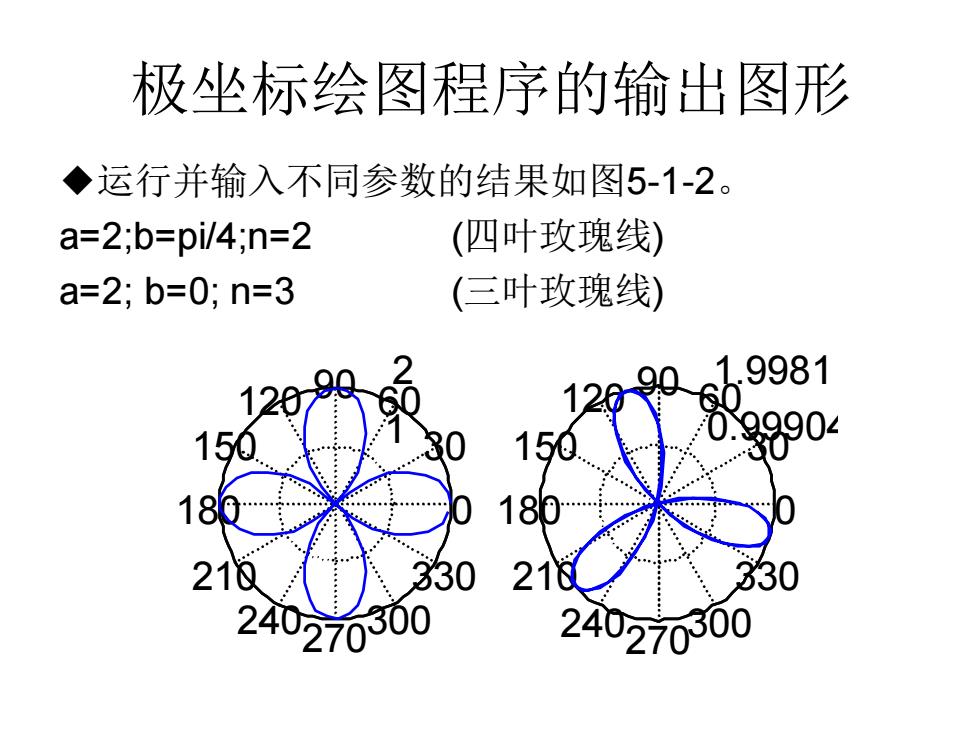
极坐标绘图程序的输出图形 ◆运行并输入不同参数的结果如图5-1-2。 a=2;b=pi/4;n=2 (四叶玫瑰线) a=2;b=0;n=3 (三叶玫瑰线) 1209 1.9981 .99904 150 150 18 18 21仅 330 21 30 240270300 24027000
极坐标绘图程序的输出图形 ◆运行并输入不同参数的结果如图5-1-2。 a=2;b=pi/4;n=2 (四叶玫瑰线) a=2; b=0; n=3 (三叶玫瑰线) 1 2 30 210 60 240 90 270 120 300 150 330 180 0 0.99904 1.9981 30 210 60 240 90 270 120 300 150 330 180 0

行星轨道的绘制 【例5-2-2】根据开普勒定律,当忽略其他天体引力,在 一个大天体引力下的小天体应该取椭圆、抛物线或双曲线 轨道。它相对于大天体的极坐标位置应满足下列方程: p=B+spcos0 其中ε为偏心率,B为常数,p为向径而阳为极角,所取 的轨道形状由偏心率决定。试画出天体轨道,讨论参数β, ε对轨道形状的影响。 ·解:◆建模:移项,将方程变换为 B 1-gcos0 其中自变量为theta,因变量为rho。beta和epsilon为参数
行星轨道的绘制 • 【例5-2-2】 根据开普勒定律,当忽略其他天体引力,在 一个大天体引力下的小天体应该取椭圆、抛物线或双曲线 轨道。它相对于大天体的极坐标位置应满足下列方程: • 其中ε为偏心率,β为常数,ρ为向径而θ为极角,所取 的轨道形状由偏心率决定。试画出天体轨道,讨论参数β, ε对轨道形状的影响。 • 解:◆建模: 移项,将方程变换为 其中自变量为theta,因变量为rho。beta和epsilon为参数。 = + cos 1 cos = −

行星轨道绘制程序exn522 theta=0:0.1:2*pi;%产生自变量向量 beta=inpute(beta=(取为1); for i=1:3 %设置小于1,等于1,大于1的三种偏心率 epsilon=input('epsilon=(依次取为0.5,1,1.5); rho=beta./(1-epsilon.*cos(heta);%求因变量 subplot(1,3,i),polar(theta,rho);%绘图 end
行星轨道绘制程序exn522 theta=0:0.1:2*pi; % 产生自变量向量 beta= input('beta= (取为1)'); for i=1:3 % 设置小于1,等于1,大于1的三种偏心率 epsilon=input('epsilon= (依次取为0.5,1,1.5)'); rho=beta./(1- epsilon.*cos(theta)); %求因变量 subplot(1,3,i),polar(theta,rho); %绘图 end
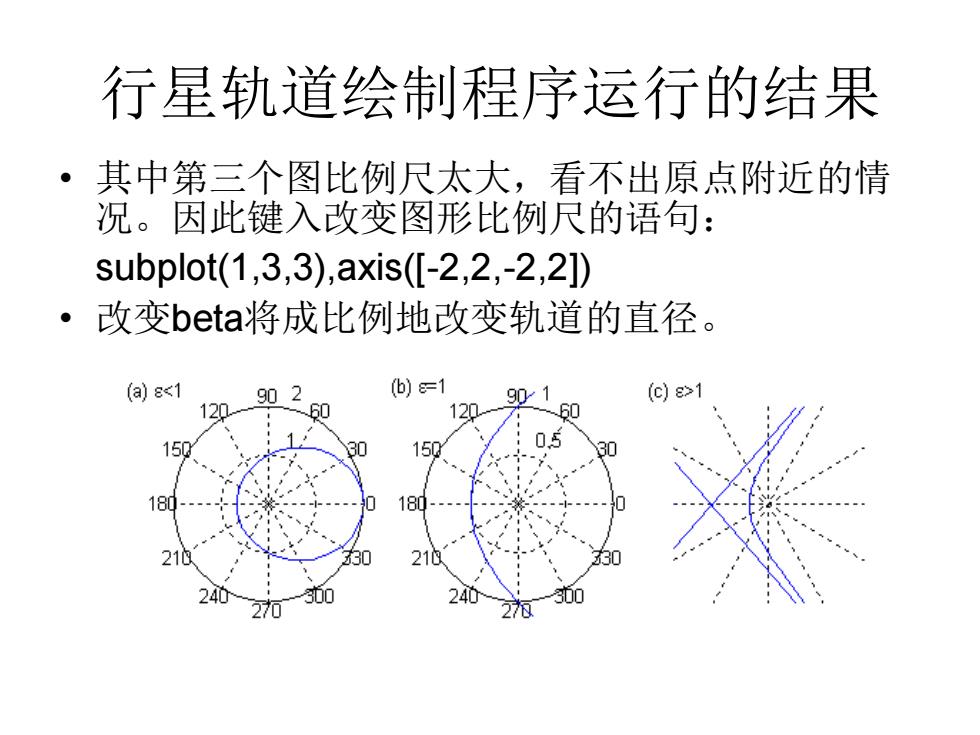
行星轨道绘制程序运行的结果 。 其中第三个图比例尺太大,看不出原点附近的情 况。因此键入改变图形比例尺的语句: subplot(1,3,3),axis(L-2,2,-2,2]) 。 改变beta将成比例地改变轨道的直径。 (a)81 120 60 20 60 150 150 05 18 181 210 21 240 240
行星轨道绘制程序运行的结果 • 其中第三个图比例尺太大,看不出原点附近的情 况。因此键入改变图形比例尺的语句: subplot(1,3,3),axis([-2,2,-2,2]) • 改变beta将成比例地改变轨道的直径

直角坐标系中椭圆的绘制 ·直角坐标中的椭圆方程为: 。 绘图时把y表示为x的显函数 a2 y=±bV1-x2/a2 ·这里正负号必须都要考虑,否则画出的椭圆就少 了一半。设a=3,b=2,程序可编写如下: x=linspace(-pi,pi,1001); %自变量数组 ·y1=2*sqt(1-x.2/32); %上半部因变量计算 ·y2=-2*sqt(1-X.2/3^2); %下半部因变量计算 plot(x,[y1;y2]),grid on %两半图都画 。axis equal %X,y轴同比例
直角坐标系中椭圆的绘制 • 直角坐标中的椭圆方程为: • 绘图时把y表示为x的显函数 • 这里正负号必须都要考虑,否则画出的椭圆就少 了一半。设a=3,b=2,程序可编写如下: • x=linspace(-pi,pi,1001); % 自变量数组 • y1=2*sqrt(1-x.^2/3^2); % 上半部因变量计算 • y2=-2*sqrt(1-x.^2/3^2); % 下半部因变量计算 • plot(x,[y1;y2]),grid on % 两半图都画 • axis equal % x,y轴同比例 2 2 2 2 1 x y a b + = 2 2 y b x a = −1 /

参数法绘制直角坐标中的椭圆 ·用参数方程的形式作图也许更为方便,因为它不 必考虑开方的正负号和出现的虚数。椭圆的参数 方程形式如下: x=acose,y=bsine 因此自变量可以设为theta,其范围为0~2π。 theta=linspace(-pi,pi,1001); plot(3*cos(theta),2*sin(theta),%省略了变量a,b grid on,axis equal ·得出的图形是一样的
参数法绘制直角坐标中的椭圆 • 用参数方程的形式作图也许更为方便,因为它不 必考虑开方的正负号和出现的虚数。椭圆的参数 方程形式如下: 因此自变量可以设为theta,其范围为0~2π。 theta= linspace(-pi,pi,1001); plot(3*cos(theta),2*sin(theta)),%省略了变量a,b grid on,axis equal • 得出的图形是一样的。 x a y b = = cos , sin