
5.6节概率论与数理统计
5.6节 概率论与数理统计

各种统计分布函数 0 表5-6-1中列出了20种分布函数,统计工具 箱提供了包括分布函数~cdf(Cumulattive Distribution Function)、概率密度函数 ~pdf(Probability Distribution Function)、分 布函数的逆函数~inv(Inverse Cumulattive Distribution Function)以及这些分布的理论 统计特性(均值和方差)计算函数~stat
一 各种统计分布函数 • 表5-6-1中列出了20种分布函数,统计工具 箱提供了包括分布函数~cdf(Cumulattive Distribution Function)、概率密度函数 ~pdf(Probability Distribution Function)、分 布函数的逆函数~inv(Inverse Cumulattive Distribution Function) 以及这些分布的理论 统计特性(均值和方差)计算函数~stat
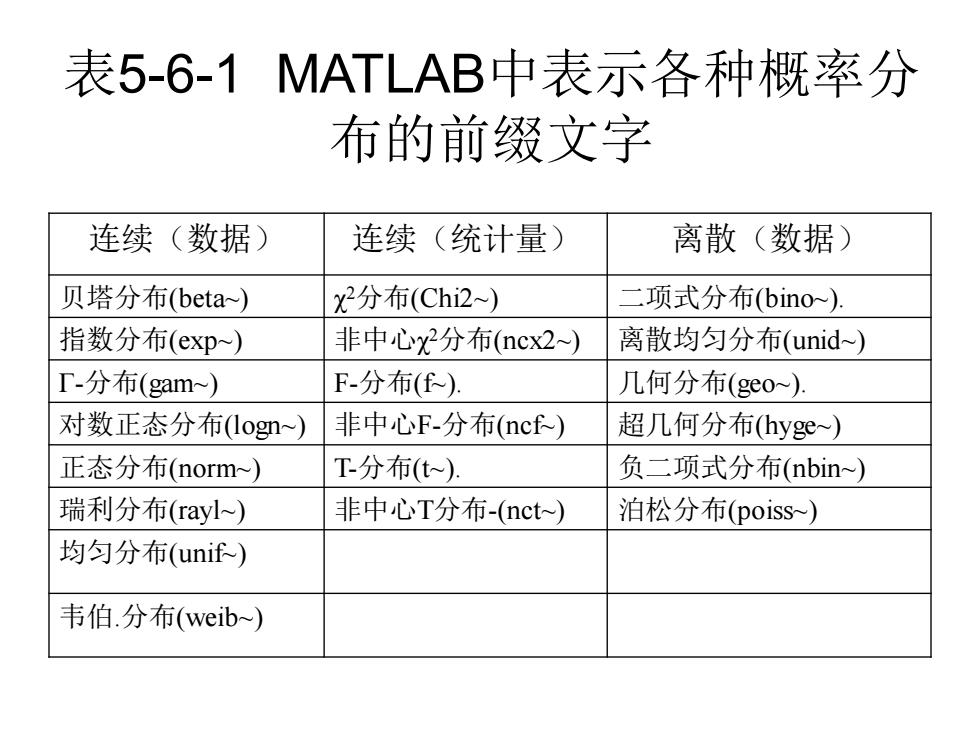
表5-6-1 MATLAB中表示各种概率分 布的前缀文字 连续(数据) 连续(统计量) 离散(数据) 贝塔分布(beta-) x2分布(Chi2~)》 二项式分布(bino~). 指数分布(exp~) 非中心x分布ncx2~) 离散均匀分布(unid~) T-分布(gam) F-分布(). 几何分布(geo~). 对数正态分布(logn~) 非中心F-分布(ncf~) 超几何分布(hyge~) 正态分布(norm) 工分布(t) 负二项式分布(nbin~) 瑞利分布(rayl~) 非中心T分布-(nct) 泊松分布(poiss) 均匀分布(unif) 韦伯.分布(weib~)
表5-6-1 MATLAB中表示各种概率分 布的前缀文字 连续(数据) 连续(统计量) 离散(数据) 贝塔分布(beta~) χ 2分布(Chi2~) 二项式分布(bino~). 指数分布(exp~) 非中心χ 2分布(ncx2~) 离散均匀分布(unid~) Г-分布(gam~) F-分布(f~). 几何分布(geo~). 对数正态分布(logn~) 非中心F-分布(ncf~) 超几何分布(hyge~) 正态分布(norm~) T-分布(t~). 负二项式分布(nbin~) 瑞利分布(rayl~) 非中心T分布-(nct~) 泊松分布(poiss~) 均匀分布(unif~) 韦伯.分布(weib~)

表5-6-1的使用方法 把表中不同分布后面括号中的文字作为前缀,把 所需计算的特性作为后缀,就可以组合成一个函 数。例如离散类的二项式分布有binopdf,binocdf, binoinv,.binostat四个函数,连续类数据的标准正 态分布有normpdf,normcdf,,norminv,normstat四 个函数,连续类统计量的X2分布有chi2pdf, chi2cdf,chi2inv,chi2stat四个函数,.等等,20 种分布就有80个函数。由于各种分布函数的解析 形式都是已知的,这些子程序的编写并不困难
表5-6-1的使用方法 • 把表中不同分布后面括号中的文字作为前缀,把 所需计算的特性作为后缀,就可以组合成一个函 数。例如离散类的二项式分布有binopdf, binocdf, binoinv, binostat四个函数,连续类数据的标准正 态分布有normpdf, normcdf, norminv, normstat四 个函数,连续类统计量的χ2分布有chi2pdf, chi2cdf, chi2inv, chi2stat四个函数,…等等,20 种分布就有80个函数。由于各种分布函数的解析 形式都是已知的,这些子程序的编写并不困难

【例5-6-1】概率分布曲线的绘制 【例5-6-1】(a)求标准正态分布N(0,1),自由度V=10的X2 分布和N=10,p=0.2的二项式分布B(10,0.2)的分布函数, 并画出其概率密度曲线和分布曲线;(b)。求出分布函数 为0.05和0.95处的随机变量值;(c).。求出这几个分布的 均值和方差。 解:分别键入help normpdf,.help binopdf,help chi2pdf以 了解它们的用法,特别是了解输入变元的意义,得知: f=normpdf(x,mu,sigma) 其中x为随机变量数组,mu为均值,sigma为标准差。 f=chi2pdf(x,V) 其中x为随机变量数组,V为自由度数(整数), f=binopdf(x,N,p) 其中x为随机变量整数数组,N为次数,0≤P≤1为成功概率
【例5-6-1】概率分布曲线的绘制 • 【例5-6-1】(a)求标准正态分布N(0,1),自由度V=10的χ 2 分布和N=10,p=0.2的二项式分布B(10,0.2)的分布函数, 并画出其概率密度曲线和分布曲线;(b) 。求出分布函数 为0.05和0.95处的随机变量值;(c) 。求出这几个分布的 均值和方差。 • 解:分别键入help normpdf, help binopdf, help chi2pdf 以 了解它们的用法,特别是了解输入变元的意义,得知: f=normpdf(x,mu,sigma) 其中x为随机变量数组,mu为均值,sigma为标准差。 f=chi2pdf(x,V) 其中x为随机变量数组,V为自由度数(整数), f=binopdf(x,N,p) 其中x为随机变量整数数组,N为次数,0≤p≤1为成功概率

概率分布参数的选择 题目中给出的变元参数应足以用来调用这些概率 密度函数,只有随机变量x的取值及范围,需要事 先对该分布的特性有所了解。首先要弄清它是离 散量还是连续量,其次要取适当的范围。范围取 小了不能显示分布的全局,取大了又可能显示不 出细节。正确的取法应该使该范围内分布函数F(X) 的左边界值略小于0.025,右边界值略大于0.975, 这就可以基本涵盖随机变量以概率95%存在的主 要区域,又不致涉及关系不大的区域。初学者往 往要作几次试探才能做到。好在在计算机上改几 个参数、作几次试探是很简便的事
概率分布参数的选择 • 题目中给出的变元参数应足以用来调用这些概率 密度函数,只有随机变量x的取值及范围,需要事 先对该分布的特性有所了解。首先要弄清它是离 散量还是连续量,其次要取适当的范围。范围取 小了不能显示分布的全局,取大了又可能显示不 出细节。正确的取法应该使该范围内分布函数F(x) 的左边界值略小于0.025,右边界值略大于0.975, 这就可以基本涵盖随机变量以概率95%存在的主 要区域,又不致涉及关系不大的区域。初学者往 往要作几次试探才能做到。好在在计算机上改几 个参数、作几次试探是很简便的事

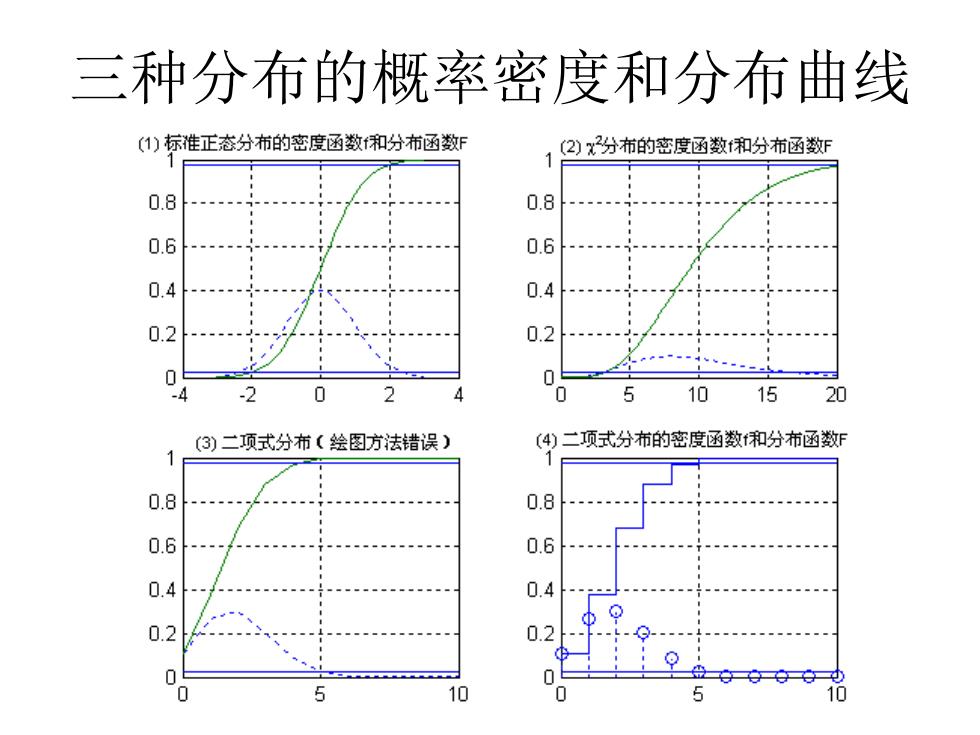
绘制概率分布函数的程序exn561 ×1=[-3:0.1:3] %标准正态随机变量取值范围 f1 normpdf(x1,0,1); %标准正态分布的概率密度函数 F1 normcdf(x1,0,1); %标准正态分布的分布函数 subplot(2,2,1),plot(x1,f1,':,x1,F1,'-),grid on %绘曲线 line([-4,4],[0.025,0.025]),1ine(-4,4],[0.975,0.975])%画横线 x2=[0:0.1:20] %试探得出的范围 f2=chi2pdf(x2,10); %X2分布的概率密度函数 F2=chi2cdf(x2,10); %X2分布的分布函数 subplot(2,2,2),plot(x2,f2,,x2,F2,-),grid on %绘曲线 line([0,20],[0.025,0.025]),line(0,20],[0.975,0.975])%画横线); 运行程序得出图5-40,其中实线是分布函数的曲线,虚线则是 密度函数的曲线。上下两根横线分别为0.975和0.025
绘制概率分布函数的程序exn561 x1 = [-3:0.1:3]; %标准正态随机变量取值范围 f1 = normpdf(x1,0,1); % 标准正态分布的概率密度函数 F1 = normcdf(x1,0,1); % 标准正态分布的分布函数 subplot(2,2,1),plot(x1,f1,':',x1,F1,'-'),grid on % 绘曲线 line([-4,4],[0.025,0.025]),line([-4,4],[0.975,0.975])% 画横线 x2 = [0:0.1:20]; % 试探得出的范围 f2 = chi2pdf(x2,10); % χ2分布的概率密度函数 F2 = chi2cdf(x2,10); % χ2分布的分布函数 subplot(2,2,2),plot(x2,f2,':',x2,F2,'-'),grid on % 绘曲线 line([0,20],[0.025,0.025]),line([0,20],[0.975,0.975]) % 画横线); ……. 运行程序得出图5-40,其中实线是分布函数的曲线,虚线则是 密度函数的曲线。上下两根横线分别为0.975和0.025
三种分布的概率密度和分布曲线 (1)标准正态分布的密度函数和分布函数F (2)分布的密度函数和分布函数F 0.8 0.8 0.6 0.6 0.4 0.4 0.2 0.2 0 -a -2 2 5 10 15 20 (3)二顶式分布(绘图方法错误) (4)二项式分布的密度函数和分布函数F 0.8 08 0.6 0.6 0.4 04 0 0.2 0.2 5 10 10
三种分布的概率密度和分布曲线

对分布函数图形的改进 。 第三个子图中,随机变量是离散取值的,在两个相邻的取 值点之间的概率不会变化,所以它的分布函数表现为阶梯 形。密度函数是分布函数的导数,所以在阶梯突变处导数 为无穷大,宽度又为无穷小,面积等于阶梯的高度,通常 用一个脉冲表示。脉冲的高度表示它所包含的面积,也就 等于阶梯波形的高度。而plot函数画图是把各离散点之间 用直线联接,所得的曲线是不对的。应该要用stairs命令 画阶梯图,用stem命令画脉冲图。改正后的程序如下: subplot(2,2,4),stairs(x3,F3,-),stem(x3,f3,) 图中第四子图给出了改正后的结果,可见其概率密度函数 是离散的脉冲。从中还可以判断,3的取值范围不必为 [0:101,取[05]就够了。另外,第二子图上的密度函数波 形太小,如果对和F取不同的纵坐标,那样可以得出更好 的图形
对分布函数图形的改进 • 第三个子图中,随机变量是离散取值的,在两个相邻的取 值点之间的概率不会变化,所以它的分布函数表现为阶梯 形。密度函数是分布函数的导数,所以在阶梯突变处导数 为无穷大,宽度又为无穷小,面积等于阶梯的高度,通常 用一个脉冲表示。脉冲的高度表示它所包含的面积,也就 等于阶梯波形的高度。而plot函数画图是把各离散点之间 用直线联接,所得的曲线是不对的。应该要用stairs命令 画阶梯图,用stem命令画脉冲图。改正后的程序如下: • subplot(2,2,4), stairs(x3,F3,'-'),stem(x3,f3,':'), • 图中第四子图给出了改正后的结果,可见其概率密度函数 是离散的脉冲。从中还可以判断,x3的取值范围不必为 [0:10],取[0:5]就够了。另外,第二子图上的密度函数波 形太小,如果对f和F取不同的纵坐标,那样可以得出更好 的图形

分布函数逆函数的用途 ·(b)给定分布函数F=a(a≤1)求出的x,简称a下分位点, 习惯上用λa表示。这和已知x求cdf恰好是逆函数的关系, 即输入变元与输出变元恰好调换了位置,对正态分布情况, 逆函数norminv的调用格式为 X=NORMINV(F,MU,SIGMA) 其中F为给定的分布函数值,而X为对应的随机变量边界值。 ·题日中给定了的两个边界值Fb=[0.05,0.95],即 Fb=[a/2,1-a/2],(a=0.10) 求对应的随机变量x的边界值劝。,随机变量在上下两个边 界值b(即[a2,入1-a2])之间取值的置信度等于1-a,其他参 数与normpdf和normcdf中的相同。对于其他分布,可依 此类推,不再赘述
分布函数逆函数的用途 • (b) 给定分布函数F=α(α1)求出的x,简称α下分位点, 习惯上用λα表示。这和已知x求cdf恰好是逆函数的关系, 即输入变元与输出变元恰好调换了位置,对正态分布情况, 逆函数norminv的调用格式为 X = NORMINV(F,MU,SIGMA) 其中F为给定的分布函数值,而X为对应的随机变量边界值。 • 题目中给定了的两个边界值Fb=[0.05,0.95],即 求对应的随机变量x的边界值xb。,随机变量在上下两个边 界值xb(即[λα/2,λ1-α/2])之间取值的置信度等于1-α,其他参 数与normpdf和normcdf中的相同。对于其他分布,可依 此类推,不再赘述。 Fb = − = [ / 2,1 / 2], ( 0.10)