
西安在子科枝大拳 电子工学院DD School of Electronic Engineering,Xidian University http://see.xidian.edu.cn edu.cn 场论与复变函数 lexuamail.x 主讲:徐乐 2011年8月30日星期

Review 场论导论 ■矢量场的矢量线 .edu.ch 单值、连续且具 数量场的等值面与等值线 有一阶连续偏导 ■数量场的方向导数与梯度 lexu@mail.xidian.edu.cn

矢量场 。M为天量场中的在意二点亿 矢量场 4=4(M) ·矢量场中分布在各点处的矢量是场点的函数 ·直角坐标系下,矢量场可表示为: A=A(x,y,z)i +A,(x,y,z2)月 +A(民,yz) lexu@mail.xidian.edu.cn
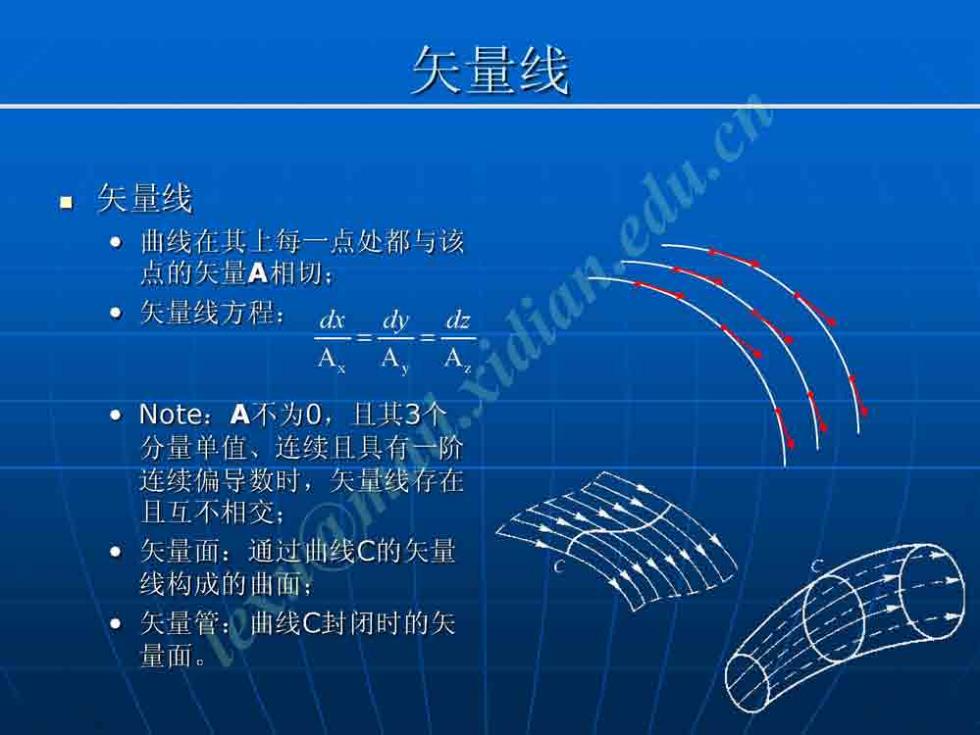
矢量线 ■矢量线 edu.cr 。曲线在其上每一点处都与该 点的东量A相切: 。矢量线方程 d dia dy dz AA、 。Note:A不为0,且其3个 分量单值、连续且具有一阶 连续偏导数时,矢量线存在 且互不相交: 矢量面:通过曲线C的矢量 线构成的曲面 矢量管:曲线C封闭时的矢 量面

等值面 ■等值面 ·在数量场中,使函数取相同数值的所有点组成的曲面 称为该数量场的等值面 ·Notel:函数单值且各连续偏导数不全为0,则等值面必 存在。 Note2:c取遍所有可能值时,这族等值面充满数量场所 在空间,且这族等值面两两互不相交。 ·Note3:数量场中的每一点都有一个等值面通过,且函 数单值,故每一个点均有且仅有一个等值面通过 lexu@mail.xidian.edu.cn

梯度 梯度性质 du.ci ·梯度与方向导数:数量场在一点沿某方向的方向导数 等于梯度在该方向的投影: ·梯度与等值面:数量场中一点处的梯度垂直于该点处 的等值面,且指向数量增大一方。 ou gradu.0 gradu= Ou Ox * ay Z lexu@mail.xidian.edu.cn
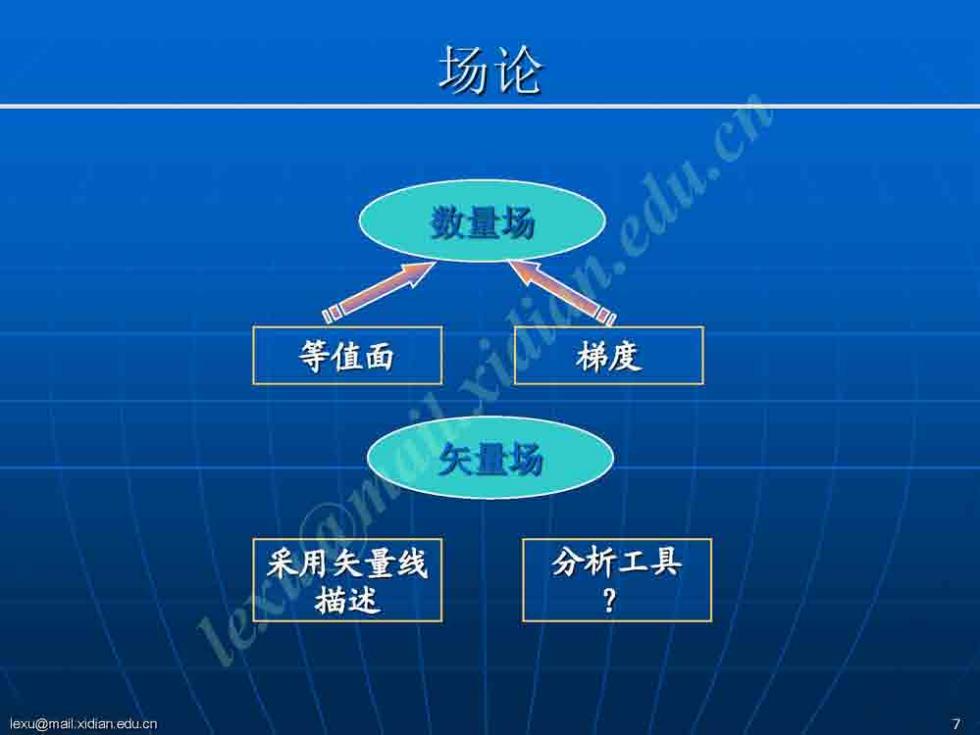
场论 数量场 n.edu.ch 0 等值面 梯度 东量场 采用夫量线 分析工具 描述 2 lexu@mail.xidian.edu.cn

/lexuqailcidian.edu.cn 第3讲矢量场分析 矢量场的通量与散度: 矢量场的通量 矢量场的散度 矢量场的环量与旋度: 矢量场的环量 矢量场的旋度 lexu@mail.xidian.edu.cn 8

矢量场的通量与散度 有向曲面 ·为区分曲面两侧,常规定其一侧为曲面的正侧,另一面 为其负侧。这种取定了正侧的曲面称为有向曲面 ·对于封闭曲面,习惯上总是取其外侧为正侧。 流量 。 设S为流速场v(M)中一一有向曲面,考虑单位时间流体向 正侧穿过S的流量Q。(正向指向S正侧) 。在S上取d,一s足够小以至手心上各点处曲面法向及流体 流矢均与M处相同。流体穿过s的流量为: dQ认=()d=下,d ·单位时间内沿正向穿过s的总流量为 Q=∬d№=.本=川.函 数学上把这种形式的曲面积分称为通量。 lexu@mail.xidian.edu.cn

矢量场的通量与散度 曲面正向 。将曲面的一个面元用矢量S来表示,其方向取为面元 的法线方向,其大小为dS,即 ds nds ·n是面元法线方向的单位矢量。 。开曲面:设这个开曲面是由封闭曲线所围成的,则选定绕行 的方向后,沿绕行方向按右手螺旋的拇指方向就是的方向 闭曲面:外侧为n的方向 lexu@mail.xidian.edu.cn 10