
场论与复变函数 复变函数篇 主讲教师:徐乐 2014年9月24日星期三
场论与复变函数 ——复变函数篇 主讲教师:徐乐 2014 年 9 月24日星期三

复数概论 必复数 冬复数的表示 冬复数的运算 冬复球面 lexu@mail.xidian.edu.cn 矩阵论●
复数概论 复数 复数的表示 复数的运算 复球面 lexu@mail.xidian.edu.cn 矩 阵 论 2

复数 为复变函数论的创建做了最早期工作的是欧 拉、达朗贝尔等先驱 冬而这门学科的发展作了大量奠基工作的是柯 西、黎曼和德国数学家维尔斯特拉斯。 从柯西算起,复变函数论已有170多年的历 史了。它以其完美的理论与精湛的技巧成为 数学的一个重要组成部分。它曾经推动过一 些学科的发展,并且常常作为一个有力的工 具被应用在实际问题中,它的基础内容已成 为理工科很多专业的必修课程。 lexu@mail.xidian.edu.cn 矩阵论
复数 为复变函数论的创建做了最早期工作的是欧 拉、达朗贝尔等先驱 而这门学科的发展作了大量奠基工作的是柯 西、黎曼和德国数学家维尔斯特拉斯。 从柯西算起,复变函数论已有170多年的历 史了。它以其完美的理论与精湛的技巧成为 数学的一个重要组成部分。它曾经推动过一 些学科的发展,并且常常作为 个有力的工 一 具被应用在实际问题中,它的基础内容已成 为理工科很多专业的必修课程。 lexu@mail.xidian.edu.cn 矩 阵 论 3 为理工科很多专业的必修课程

复数 冬复变函数的应用涉及面很广 ■可以用来解决复杂的计算 ■物理学上有很多不同的稳定平面场,对它们的 计算就是通过复变函数来解决的。 ·俄国的茹柯夫斯基在设计飞机的时候,就用复 变函数论解决了飞机机翼的结构问题,他在运 用复变函数论解决流体力学和航空力学方面的 问题上也做出了贡献。 lexu@mail.xidian.edu.cn 矩阵论
复数 复变函数的应用涉及面很广 可以用来解决复杂的计算 物理学上有很多不同的稳定平面场,对它们的 计算就是通过复变函数来解决的。 俄国的茹柯夫斯基在设计飞机的时候,就用复 变函数论解决了飞机机翼的结构问题,他在运 用复变 数论解决流体力学 航 力学 的 复变函数论解决流体力学和航空力学方面的 问题上也做出了贡献。 lexu@mail.xidian.edu.cn 矩 阵 论 4
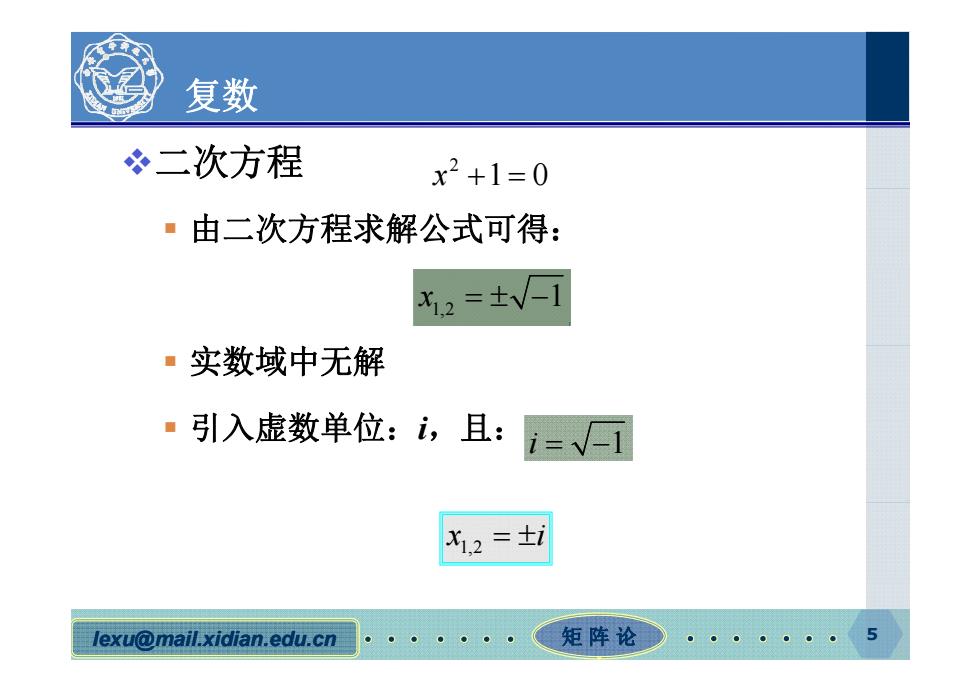
复数 冬二次方程 x2+1=0 ·由二次方程求解公式可得: X12 =tv-1 ·实数域中无解 ·引入虚数单位:i,且: i= 水2=i lexu@mail.xidian.edu.cn 矩阵论
复数 二次方程 1 0 2 x 由二次方程求解公式可得: 1,2 x 1 实数域中无解 引入虚数单位:i,且:i 1 1,2 x i lexu@mail.xidian.edu.cn 矩 阵 论 5
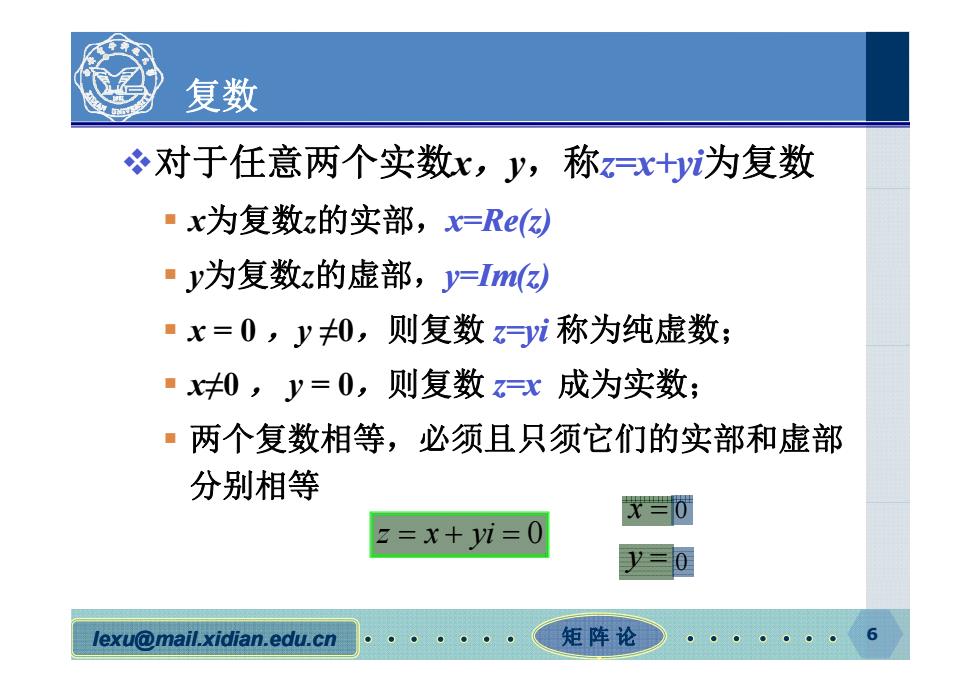
复数 对于任意两个实数x,y,称z=x+y为复数 ·x为复数z的实部,x=Re() ■y为复数z的虚部,y=m) ·x=0,y0,则复数y称为纯虚数; ·0,y=0,则复数x成为实数; ·两个复数相等,必须且只须它们的实部和虚部 分别相等 元0 2=x+yi=0 y=0 lexu@mail.xidian.edu.cn 矩阵论 6
复数 对于任意两个实数x,y,称z=x+yi为复数 x为复数z的实部,x=Re(z) y为复数z的虚部,y=I () m z x = 0 ,y ≠0,则复数 z=yi 称为纯虚数; x≠0 , y = 0,则复数 z=x 成为实数; 两个复数相等,必须 只须它们的实部和虚部 必须且只须它们的实部和虚部 分别相等 0 z x yi 0 x y 0 0 lexu@mail.xidian.edu.cn 矩 阵 论 6
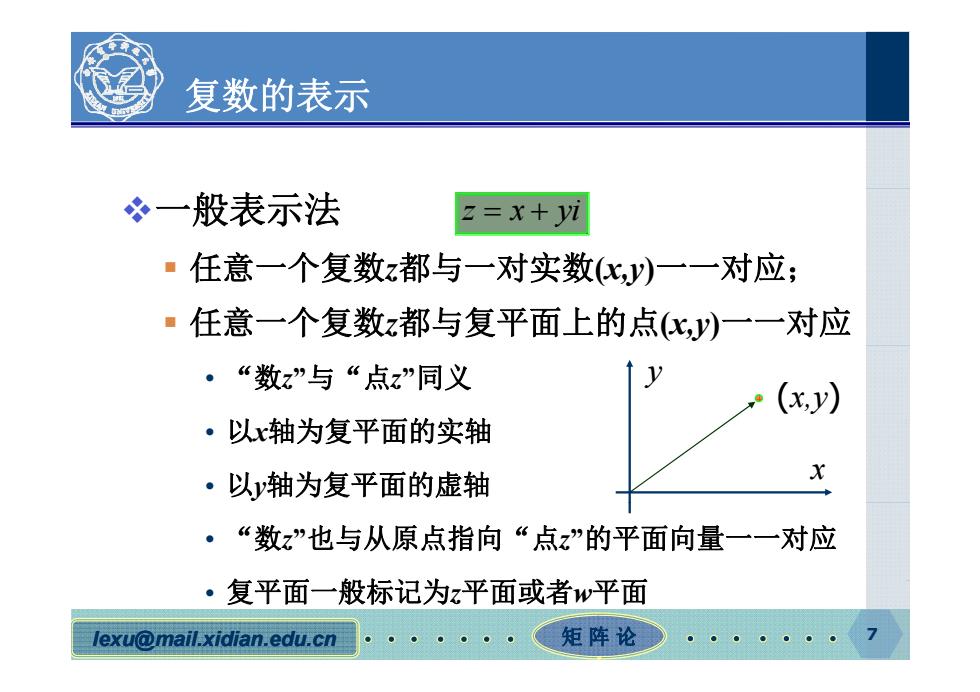
复数的表示 冬一般表示法 z=x+yi ·任意一个复数z都与一对实数(飞,y)一一对应; ■任意一个复数z都与复平面上的点化,y)一一对应 ·“数z”与“点z”同义 (x,y) ·以x轴为复平面的实轴 ·以y轴为复平面的虚轴 ·“数z”也与从原点指向“点z”的平面向量一一对应 ·复平面一般标记为z平面或者w平面 lexu@mail.xidian.edu.cn 矩阵论
复数的表示 一般表示法 任意一个复数z都与一对实数(x y)一一对应 z x yi 任意 个复数z都与 对实数(x,y) 对应; 任意一个复数z都与复平面上的点(x,y)一一对应 • “数z”与“点z”同义 以 轴为复平面的实轴 y (x,y) • 以x轴为复平面的实轴 • 以y轴为复平面的虚轴 x • “数z”也与从原点指向“点z”的平面向量一一对应 复平面 般标记为 平面或者 平面 lexu@mail.xidian.edu.cn 矩 阵 论 7 • 复平面一般标记为z平面或者w平面
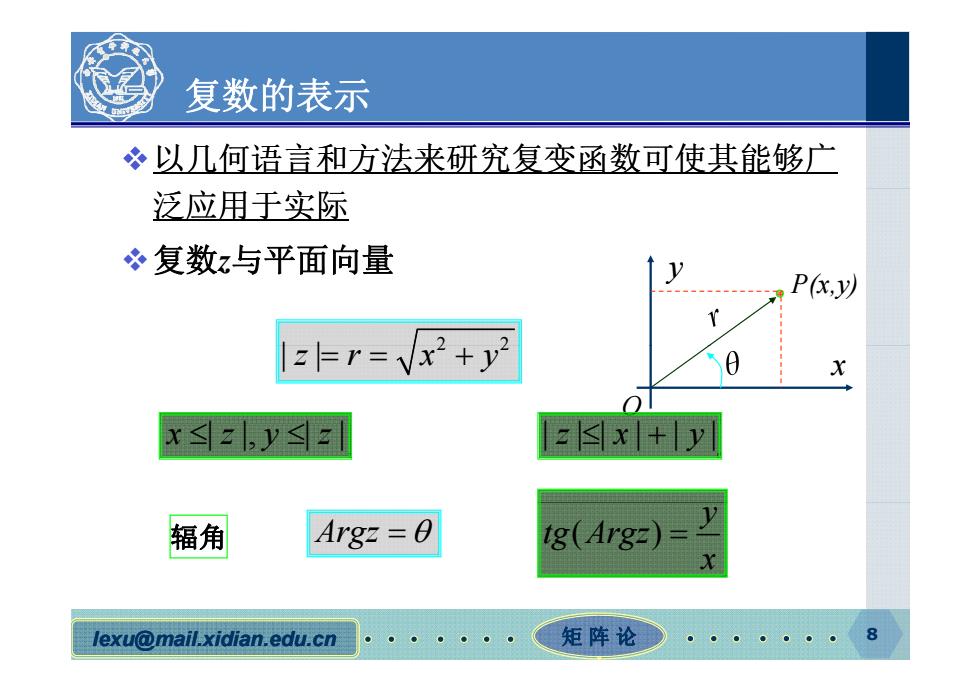
复数的表示 ·以几何语言和方法来研究复变函数可使其能够广 泛应用于实际 复数z与平面向量 PK,y以 |z=r=、 /x2+y2 0 xz,y≤z x+ly 辐角 Argz =0 I8(Arg=)= lexu@mail.xidian.edu.cn 矩阵论D 8
复数的表示 以几何语言和方法来研究复变函数可使其能够广 泛应用于实际 复数z与平面向量 y P(x,y) 2 2 | | x O z r xy x zy z || || , | || | | | | || | | | z x y Argz ( ) y tg Argz x 辐角 lexu@mail.xidian.edu.cn 矩 阵 论 8
复数的表示 冬辐角 0时,以正实轴为始边,表示z的向量为终边的角0的 弧度称为z的辐角 ·z=0时,辐角不确定 ·任何一个0时的复数,辐角无穷多 Argz=O,+2kπ 辐角主值 ·在z(0)的辐角中,满足-π<0,≤r的0称为Agz的主值, 记作 00 argz lexu@mail.xidian.edu.cn 矩阵论
复数的表示 辐角 z≠0时,以正实轴为始边,表示z的向量为终边的角θ的 弧度称为z的辐角 z =0时,辐角不确定 任何一个z≠0时的复数,辐角无穷多 辐角主值 1 Argz k 2 辐角主值 在z(≠0)的辐角中,满足-π<θ0≤π的θ0称为Argz的主值, 记作 0 argz lexu@mail.xidian.edu.cn 矩 阵 论 9
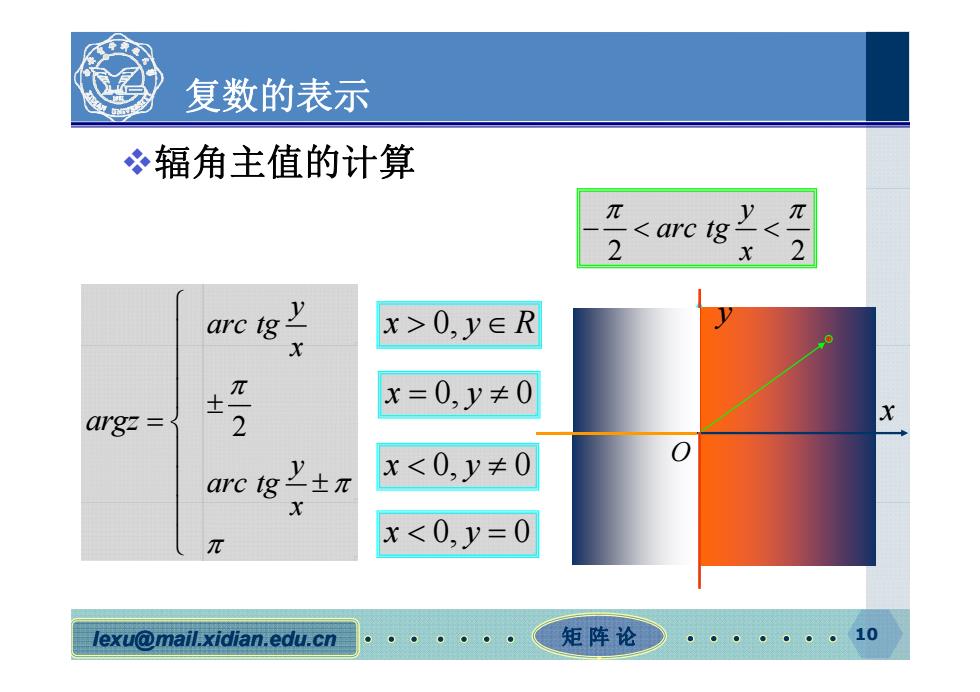
复数的表示 辐角主值的计算 0,y∈R x x=0,y≠0 argz 2 arcg'±z x<0,y≠0 X π x<0,y=0 lexu@mail.xidian.edu.cn 矩阵论 。。··。·。10
复数的表示 辐角主值的计算 2 2 y arc tg x y x yR 0, y arc tg x argz x x y 0, 0 2 x argz O x y 0, 0 2 y arc tg x x y 0, 0 x lexu@mail.xidian.edu.cn 矩 阵 论 10