
场论与复变函数 主讲:徐乐 2016年11月17日星期四
2016年11月17日星期四 场论与复变函数 主讲:徐乐

复变函数 课程的教学目标与任务 ·是高等学校工科类专业的一门重要的基础理论课 ·是研究复变量函数的分析课程 冬通过本课程的学习 ·使学生掌握复变函数的基本理论与方法 ·了解复变函数在后续数学课程(如积分变换、数学物理 方程)中的应用以及在解决实际问题中的应用 ·培养学生应用复变函数的知识解决本专业实际问题的 能力 lexu@mail.xidian.edu.cn 复变函数●
lexu@mail.xidian.edu.cn 复变函数 复变函数 v课程的教学目标与任务 § 是高等学校工科类专业的一门重要的基础理论课 § 是研究复变量函数的分析课程 v通过本课程的学习 § 使学生掌握复变函数的基本理论与方法 § 了解复变函数在后续数学课程(如积分变换、数学物理 方程)中的应用以及在解决实际问题中的应用 § 培养学生应用复变函数的知识解决本专业实际问题的 能力

复变函数 本课程与其它课程的联系和分工 复变函数是介于基础理论和工程技术的中间课 程 ·是自然科学与工程技术中常用的数学工具 ·复变函数与高等数学中的许多概念、理论和方 法有相同之处,但又有其固有的特性 ·是微分方程、奇异积分方程和计算数学等数学 分支的主要解析方法 ·是解决诸如流体力学、电磁学、热学、弹性理 论中平面问题的有利工具 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn 复变函数 复变函数 v本课程与其它课程的联系和分工 § 复变函数是介于基础理论和工程技术的中间课 程 § 是自然科学与工程技术中常用的数学工具 § 复变函数与高等数学中的许多概念、理论和方 法有相同之处,但又有其固有的特性 § 是微分方程、奇异积分方程和计算数学等数学 分支的主要解析方法 § 是解决诸如流体力学、电磁学、热学、弹性理 论中平面问题的有利工具

课程内容及基本要求 复数与复变函数(4学时) 复数的表示方法及其代数运算、复平面区域,复球面与无穷远点 复变函数的概念、复变函数的极限和连续性。 1.基本要求 ·了解复数的概念,掌握复数的各种表示方法及其运算,理解复数 运算的几何意义、掌握用复变量方程表示常用曲线及用不等式表 示区域。 ·了解区域、单连通域、多连通域和复球面等概念。 ·理解复变函数概念,了解复变函数的极限与连续的概念。 2.重点、难点 ·重点:复数的各种表示方法及其运算。 ·难点:复变函数极限的概念。 ÷3.说明 本章是学习后面内容的基础。同时注意复变函数及其极限、连续 与高等数学中相应概念的联系与区别。 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn 复变函数 课程内容及基本要求 v 复数与复变函数(4学时) § 复数的表示方法及其代数运算、复平面区域,复球面与无穷远点 § 复变函数的概念、复变函数的极限和连续性。 v 1. 基本要求 § 了解复数的概念,掌握复数的各种表示方法及其运算,理解复数 运算的几何意义、掌握用复变量方程表示常用曲线及用不等式表 示区域。 § 了解区域、单连通域、多连通域和复球面等概念。 § 理解复变函数概念,了解复变函数的极限与连续的概念。 v 2. 重点、难点 § 重点:复数的各种表示方法及其运算。 § 难点:复变函数极限的概念。 v 3. 说明 § 本章是学习后面内容的基础。同时注意复变函数及其极限、连续 与高等数学中相应概念的联系与区别

课程内容及基本要求 解析函数(6学时) 复变函数的导数及解析函数的概念;函数解析的充分必要条件; 初等函数及其解析性质;平面场的复势 基本要求 n 理解复变函数导数、解析的概念、掌握复变函数解析的充分必要 条件及判别函数解析性的方法 ·了解初等函数(指数函数、三角函数、对数函数、幂函数)的定义 及解析性质 ·了解平面场的复势。 冬重点、难点 ·重点:复变函数解析的概念及判别方法。 ·难点:复变函数解析的概念。 女说明 ■ 解析函数是复变函数研究主要对象,是学习本课程重点掌握内容 之一。 lexu@mail.xidian.edu.cn 复变函数●
lexu@mail.xidian.edu.cn 复变函数 课程内容及基本要求 v 解析函数(6学时) § 复变函数的导数及解析函数的概念;函数解析的充分必要条件; § 初等函数及其解析性质;平面场的复势 v 基本要求 § 理解复变函数导数、解析的概念、掌握复变函数解析的充分必要 条件及判别函数解析性的方法 § 了解初等函数(指数函数、三角函数、对数函数、幂函数)的定义 及解析性质 § 了解平面场的复势。 v 重点、难点 § 重点:复变函数解析的概念及判别方法。 § 难点:复变函数解析的概念。 v 说明 § 解析函数是复变函数研究主要对象,是学习本课程重点掌握内容 之一

课程内容及基本要求 复变函数的积分(6学时) 复变函数积分的定义、性质和计算;柯西一古萨(Cauchy一Goursat)基本 定理及其推广;复合闭路定理;柯西(Cauchy)积分公式及解析函数的高 阶导数; ·解析函数与调和函数的关系。 基本要求 ■ 理解复变函数积分的概念,掌握复变函数积分的基本性质及一般计算方 法、理解柯西一古萨基本定理及其推论 ·熟练掌握用柯西积分公式及高阶导数公式计算积分的方法、了解摩勒拉 (Morera)定理。 ·了解调和函数与解析函数的关系,会从解析函数的实(虚)部求其虚(实)部。 冬重点、难点 ·柯西一古萨基本定理及柯西积分公式。 ·摩勒拉(Morera)定理。 冬说明 本章内容是整个复变函数理论的基础。 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn 复变函数 课程内容及基本要求 v 复变函数的积分(6学时) § 复变函数积分的定义、性质和计算;柯西-古萨(Cauchy-Goursat)基本 定理及其推广;复合闭路定理;柯西(Cauchy)积分公式及解析函数的高 阶导数; § 解析函数与调和函数的关系。 v 基本要求 § 理解复变函数积分的概念,掌握复变函数积分的基本性质及一般计算方 法、理解柯西-古萨基本定理及其推论 § 熟练掌握用柯西积分公式及高阶导数公式计算积分的方法、了解摩勒拉 (Morera)定理。 § 了解调和函数与解析函数的关系,会从解析函数的实(虚)部求其虚(实)部。 v 重点、难点 § 柯西-古萨基本定理及柯西积分公式。 § 摩勒拉(Morera)定理。 v 说明 § 本章内容是整个复变函数理论的基础

复数与复变函数 ·复数 i=团 复数的表示 z=x+yi z=r(cos0+isin0) 2=re0 复数的运算 are x>0,y∈R x ·复数加减 ■复数乘除 x=0,y≠0 argz ·复数共轭 ·复数乘幂与方根 aeg'±z x<0,y≠0 x π x<0,y=0 冬复球面 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn 复变函数 复数与复变函数 v复数 v复数的表示 v复数的运算 § 复数加减 § 复数乘除 § 复数共轭 § 复数乘幂与方根 v复球面 i 1 z x yi z r i (cos sin ) i z re x y R 0, x y 0, 0 x y 0, 0 x y 0, 0 argz 2 y arc tg x y arc tg x
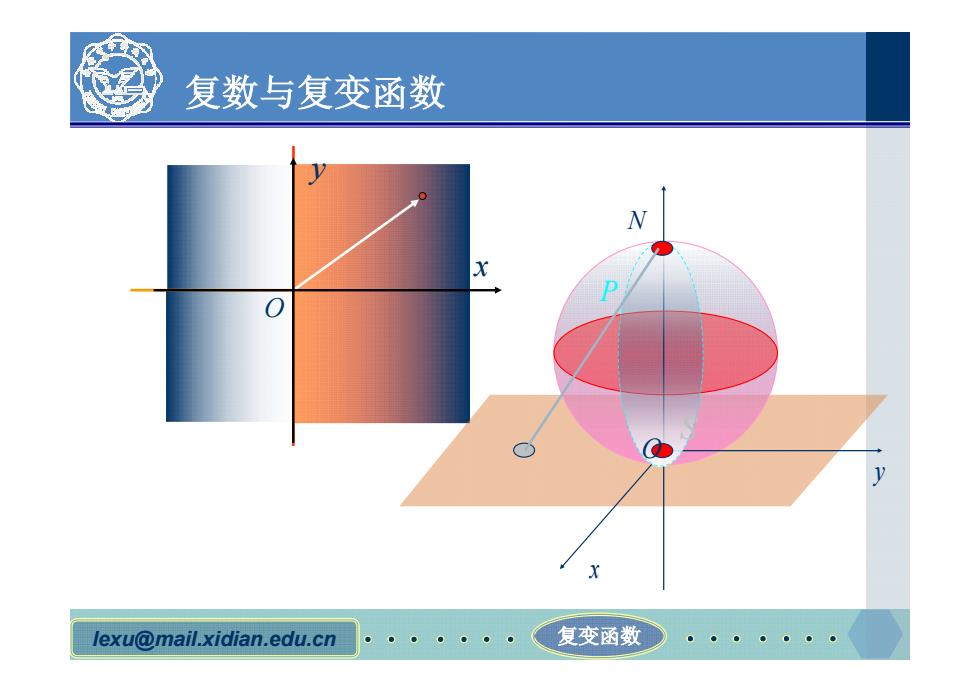
江 复数与复变函数 X lexu@mail.xidian.edu.cn 复变函数●)
lexu@mail.xidian.edu.cn 复变函数 复数与复变函数 x y N O S P x y O
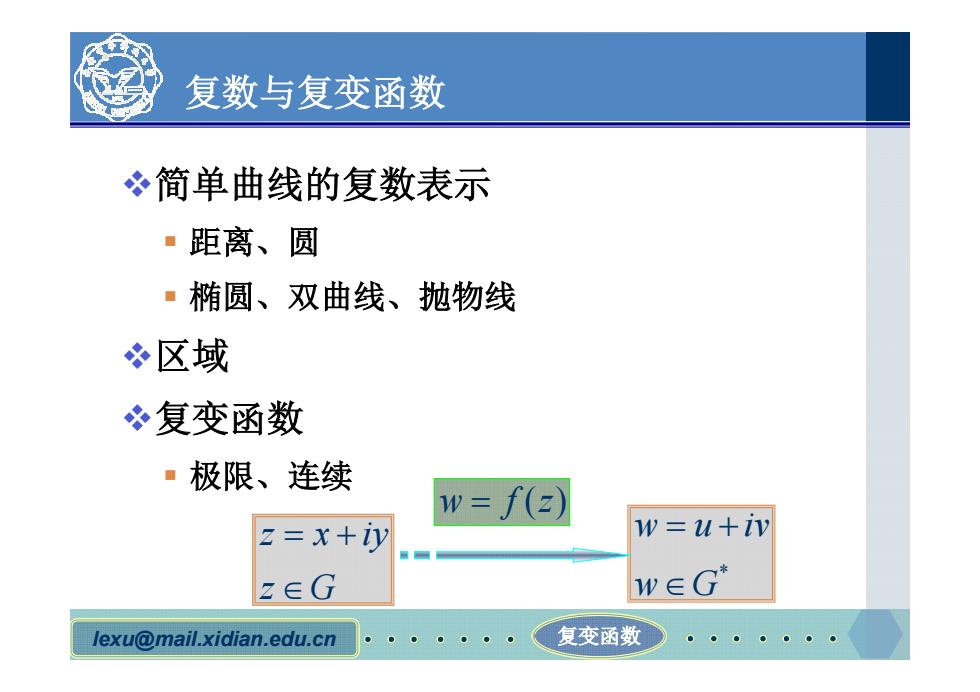
复数与复变函数 简单曲线的复数表示 ·距离、圆 ·椭圆、双曲线、抛物线 区域 冬复变函数 ·极限、连续 w=f() z=x+iy w=u+iv z∈G w∈G lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn 复变函数 复数与复变函数 v简单曲线的复数表示 § 距离、圆 § 椭圆、双曲线、抛物线 v区域 v复变函数 § 极限、连续 w f z ( ) z x iy z G * w u iv w G
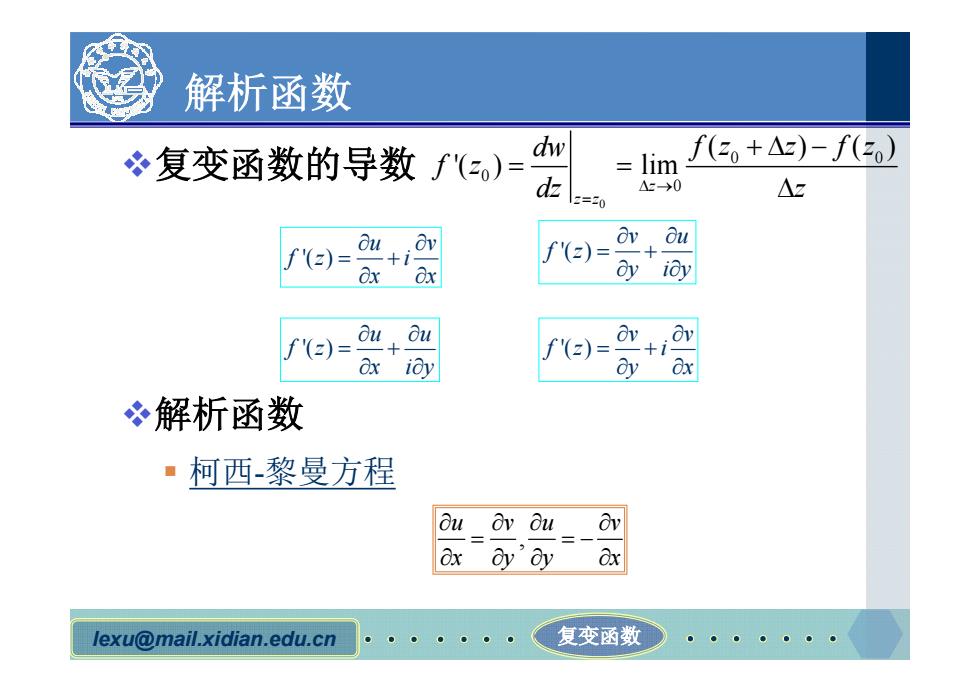
解析函数 冬复变函数的导数f()= dw lim f2+△)-f(3o) d- △x-→0 -=20 △z Ov Ou f'(z)= -+i f'(2)= ay ioy f'(z)= Ox idy f'(z)= dyox 解析函数 ·柯西-黎曼方程 ou Ov Ou Ov ax oy'ay Ox lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn 复变函数 解析函数 v复变函数的导数 v解析函数 § 柯西-黎曼方程 0 0 0 0 0 ( ) ( ) '( ) lim z z z dw f z z f z f z dz z , u v u v x y y x '( ) u v f z i x x '( ) v u f z y i y '( ) u u f z x i y '( ) v v f z i y x