
1931 矩阵论 主讲教师:徐乐 2014年10月29日星期三
2014年10月29日星期三 矩 阵 论 主讲教师:徐乐

上讲回顾 第四讲线性变换矩阵及其对角化 ■线性变换的矩阵表示 ·线性变换及矩阵的值域和核 ·特征值和特征向量 ·矩阵对角化的充要条件 lexu@mail.xidian.edu.cn 矩阵论 。。。·。。。2
lexu@mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第四 讲 线性变换矩阵及其对角化 线性变换的矩阵表示 线性变换及矩阵的值域和核 特征值和特征向量 矩阵对角化的充要条件
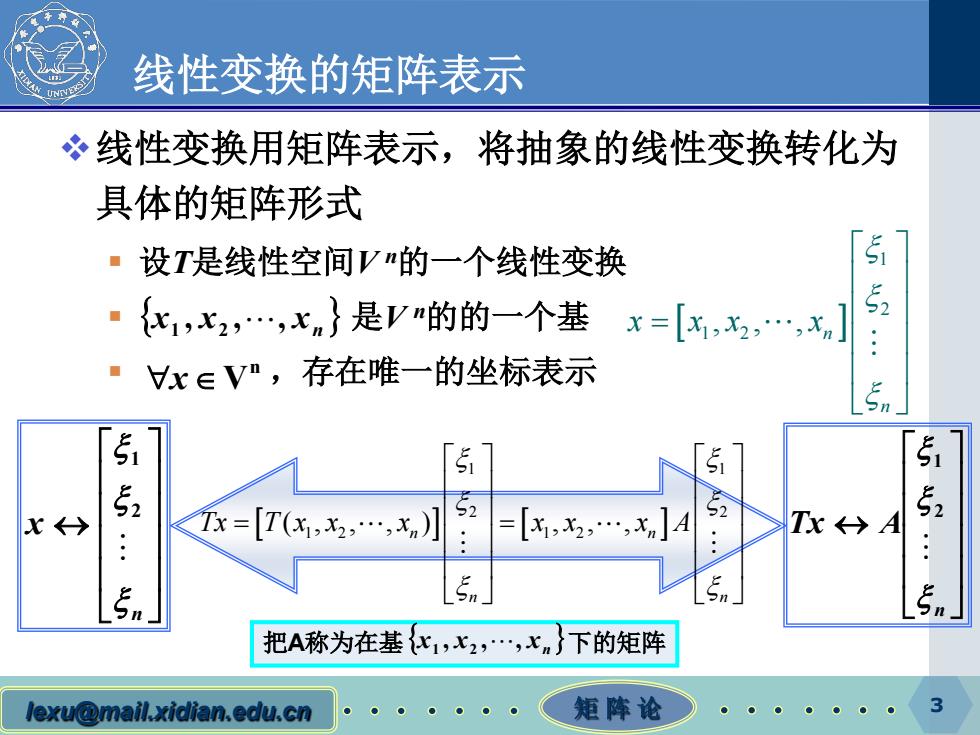
线性变换的矩阵表示 线性变换用矩阵表示,将抽象的线性变换转化为 具体的矩阵形式 ·设T是线性空间V"的一个线性变换 51 。{x1,x2,…,xn}是V"的的一个基 x=[x1,x2,…,Xn 52 x∈Vm,存在唯一的坐标表示 51 5 52 X←> Tx=[T(x,2,…,xn)】 =[x,x,…,x]A TxA 把A称为在基化1,x2,…,xn}下的矩阵 lexu@mail.xidian.edu.cn 矩阵论 ● 3
lexu@mail.xidian.edu.cn 矩 阵 论 3 线性变换的矩阵表示 线性变换用矩阵表示,将抽象的线性变换转化为 具体的矩阵形式 设T是线性空间V n的一个线性变换 是V n的的一个基 ,存在唯一的坐标表示 {x1 , x2 ,, xn } n ∀ ∈x V [ ] 1 2 1 2 ,,, n n x xx x ξ ξ ξ = [ ] [ ] 1 1 2 2 1 2 1 2 (, , , ) , , , n n n n Tx T x x x x x x A ξ ξ ξ ξ ξ ξ = = ↔ n x ξ ξ ξ 2 1 ↔ n Tx A ξ ξ ξ 2 1 把A称为在基 {x1 , x2 ,, xn }下的矩阵

线性变换的矩阵表示 冬相似矩阵 ■设T在V的两个基的矩阵分别为A和B {1,x2,…,xn} {i,x2,…,xn} ·且ki,,,x]=k,,,xn则 B=C-AC ·即A和B为相似矩阵 冬定理 ·n阶方阵A和B相似的充要条件是A和B为同一线 性变换在不同基下的矩阵 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 4 线性变换的矩阵表示 相似矩阵 设T在V n的两个基的矩阵分别为A和B 且 则 即A和B为相似矩阵 定理 n阶方阵A和B相似的充要条件是A和B为同一线 性变换在不同基下的矩阵 {x1 , x2 ,, xn } { } ' ' 2 ' 1 , , , x x xn [x , x , , xn ] [x1 , x2 , , xn ]C ' ' 2 ' 1 = 1 B C AC − =

线性变换及矩阵的值域和核 冬定义 ■设T是线性空间V"的线性变换,称 R(T)={xxeV}为T的值域 dim R(T) ·N(T)={x|x∈V",Ix=0}为T的核 dim NT) 『的秩和零度 ■R(T和N(T均为Vn的子空间 设A为mXn阶矩阵,称 ·R(A)={Ax|x∈R"orx∈C"} 为矩阵4A的值域 ·N(A)={xlx∈R"or x∈C,Ax=0为矩阵A的核 dim R(A) dim N(A) A的秩和零度 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 5 线性变换及矩阵的值域和核 定义 设T是线性空间V n的线性变换,称 • 为T的值域 • 为T的核 R(T)和N(T)均为V n的子空间 设A为m×n阶矩阵,称 • 为矩阵A的值域 • 为矩阵A的核 { }n R T Tx x () | V = ∈ { } n N T x x Tx ( ) | V, 0 =∈ = { } n n R A Ax x x ( ) | R or C =∈ ∈ { } n n N A x x x Ax ( ) | R or C , 0 =∈ ∈ = dim R(T) dim N(T) dim R(A) dim N(A) T的秩和零度 A的秩和零度

特征值与特征向量 冬定义: ·对m阶方阵A,若存在数,及非零向量(列向量)x ·使得Ax=x trA=∑ detA=Π ·则称为A的特征值 i=l ·x为A的属于特征值的特征向量 ·特征向量不唯一 A的特征多项式 ·特征向量非零 ·(I-)x=0有非零解,则det(I-A)=0 阶方阵A可通过相似变换对角化的充要条件是 它具有n个线性无关的特征向量 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 6 特征值与特征向量 定义: 对m阶方阵A,若存在数λ,及非零向量(列向量)x 使得Ax = λx 则称λ为A的特征值 x为A的属于特征值λ的特征向量 • 特征向量不唯一 • 特征向量非零 • (λI - A) x = 0有非零解,则det (λI - A) = 0 A的特征多项式 1 tr n i i A λ = = ∑ 1 det n i i A λ = = ∏ n阶方阵A可通过相似变换对角化的充要条件是 它具有n个线性无关的特征向量

第四讲矩阵对角化 冬内积空间 冬正规矩阵 冬酉对角化 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 7 第四讲 矩阵对角化 内积空间 正规矩阵 酉对角化

内积空间 冬Euclid空间 一定义 ·设V是实线性空间(k∈R),对于V中任何两个元素、 y均按某一规则存在一个实数与之对应,记为x,),若 它满足以下四个性质,则称x,y)为x与y的内积,定义 了内积的实线性空间称为Euclid空间 ·(1)交换律(c,y)=0,) ·(2)分配律(c,y+z=c,y)+(c,) ·(3)齐次律(c,y)=k(,y) ▣(4)非负性,c,x)≥0 ·当且仅当x=0时,cx)=0 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 8 内积空间 Euclid空间 ——定义 设V是实线性空间(k∈R),对于V中任何两个元素x、 y均按某一规则存在一个实数与之对应,记为(x , y),若 它满足以下四个性质,则称(x , y)为x与y的内积,定义 了内积的实线性空间称为Euclid空间 (1)交换律 (x , y)= (y, x) (2)分配律 (x , y + z)= (x , y)+ (x , z) (3)齐次律 (kx , y) = k (x , y) (4)非负性 , (x , x)≥0 • 当且仅当x=0时, (x ,x)=0

内积空间 对于一个给定的线性空间,可以定义多种 内积,较典型的如三维向量空间的数量积 就满足以上四条性质,构成内积 必以n维向量空间为例 x=[552…5n]yy=n1n2…nn] 定义内积(x,y)=∑",5n lexu@mail.xidian.edu.cn 矩阵论 9
lexu@mail.xidian.edu.cn 矩 阵 论 9 内积空间 对于一个给定的线性空间,可以定义多种 内积,较典型的如三维向量空间的数量积 就满足以上四条性质,构成内积 以n维向量空间为例 定义内积 [ ] T n x = ξ 1 ξ 2 ξ [ ] T n y = η1 η 2 η ( ) 1 , n iii i xy w ξ η = = ∑

内积空间 ·验证内积的四条性质 1D(x,川=2初=2n5=(,刘白 交换律 分配律 2)(x,y+)=立5+s)=5n+2m=(x,川+(x, (3)(,川=2(5m=k2"5=(,月月 齐次律 (4)(x)=2,5≥0当且仅当x=0时,(x,x)=0→ 非负性 lexu@mail.xidian.edu.cn 矩阵论 °。。。。10
lexu@mail.xidian.edu.cn 矩 阵 论 10 内积空间 验证内积的四条性质