
UNIVE 矩阵论 主讲教师:徐乐 2014年12月10日星期三
2014年12月10日星期三 矩 阵 论 主讲教师:徐乐

上讲回顾 冬第16讲Penrose广义逆的性质 ·{-逆的性质 。{1}-逆与{1,2}-逆 lexu@mail.xidian.edu.cn 矩阵论
2 lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第16讲 Penrose广义逆的性质 {1}-逆的性质 {1}-逆与{1,2}-逆

{1}-逆的性质 引理:rank(AB)≤min(rankA,rank B) 冬定理 ·设AeCm,BeC入eC,=h λ≠0 0 λ=0 rank(A)≥rankA (A)H∈AH{I AD∈(LA)KI} ·则 TAS1∈(SAT)I,(S∈Cmxm,T∈C") lexu@mail.xidian.edu.cn 矩阵论
3 lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 {1}-逆的性质 引理: 定理 设 则 rank(AB) min (rankA,rank B ) mn nP A C ,B C 1 † 0 C, 0 0 (1) H H (A ) A {1} † (1) A ( A){1} 1 (1) 1 m m n n T A S (SAT){1} , (S C , T C ) m n (1) rank(A ) rankA

{1}-逆的性质 AA四和AA均为幂等矩阵且与A同秩(P2=P) R(AA)=R(A),N(AA)=N(A),R((AA)B)=R(AH) AA=I.台rank(A)=n AAa)=Im台Iank(A)=m AB(AB)四A=A台rank(AB)=rank(A) B(AB)(1AB=B rank(AB)=rank(B) 定理 ·矩阵A当且仅当A为满秩方阵时具有唯一的{I逆A(山=A1 lexu@mail.xidian.edu.cn 矩阵论
4 lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 {1}-逆的性质 定理 • 矩阵A当且仅当A 为满秩方阵时具有唯一的{1}逆 (1) 1 A A

{1}-逆与{1,2}-逆 冬定理1 ·设Y,Z∈A{1,则YAZ∈A{1,2} 冬定理2 ·给定矩阵A及Z∈A{1,则Z∈A{1,2的充要 条件是rank(A)=rank(Z lexu@mail.xidian.edu.cn 矩阵论
5 lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 {1}-逆与{1,2}-逆 定理1 设 Y , Z ∈A{1}, 则YAZ ∈ A {1,2} 定理 2 给定矩阵A及Z ∈A{1}, 则Z ∈A{1,2}的充要 条件是 rank(A)=rank(Z)

第17讲Penrose广义逆与Moore广义逆 {1}-逆与{1,2,3}-逆、{1,2,4}-逆 冬关于A+ 广义逆的计算 。由Hermite标准形求{-逆 ·由满秩分解求广义逆 投影矩阵与Moore-.Penrosej逆 ·投影算子与投影矩阵 ·正交投影算子与正交投影矩阵 ·投影矩阵与广义逆矩阵 lexu@mail.xidian.edu.cn 矩阵论
6 lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 第17讲 Penrose广义逆与Moore广义逆 {1}-逆与{1,2,3}-逆、 {1,2,4}-逆 关于A+ 广义逆的计算 由Hermite标准形求{1}-逆 由满秩分解求广义逆 投影矩阵与Moore-Penrose逆 投影算子与投影矩阵 正交投影算子与正交投影矩阵 投影矩阵与广义逆矩阵
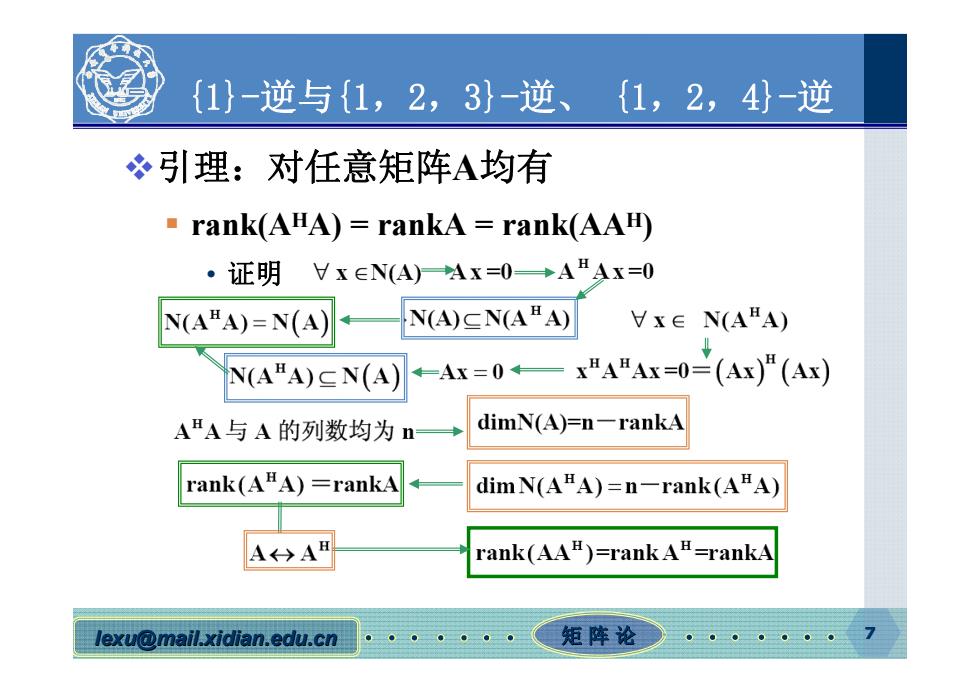
1}-逆与{1,2,3}-逆、{1,2,4}-逆 引理:对任意矩阵A均有 rank(AHA)=rankA rank(AAH) ·证明 HxeN(A)Ax=0→AHAx=0 N(AHA)=N(A) N(A)N(ABA) Hx∈N(AHA) N(AA)N(A) 4=Ax=04— x"AAx=0=(Ax)"(Ax) AA与A的列数均为n→ dimN(A)=n-rankA rank(AA)=rankA dim N(AHA)=n-rank(AA) AA rank(AAB)=rank A=rankA lexu@mail.xidian.edu.cn 矩阵论香
7 lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 7 {1}-逆与{1,2,3}-逆、 {1,2,4}-逆 引理:对任意矩阵A均有 rank(AHA) = rankA = rank(AAH) • 证明

{1}-逆与{1,2,3}-逆、{1,2,4}-逆 定理3:给定矩阵A,则 Y=(AHA)AH∈A{1,2,3} Z=AH(AAH)∈A{1,2,4 ·证明显然R(AA)CR(A)由引理可知R(AA)=R(A) A=UHAHA存在U使 AH-AHAU (i) AYA=(UHAHA)[(AHA)四A]A=UHAHA=A满足(① YEA 1 lexu@mail.xidian.edu.cn 矩阵论
8 lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 {1}-逆与{1,2,3}-逆、 {1,2,4}-逆 定理3: 给定矩阵A , 则 证明
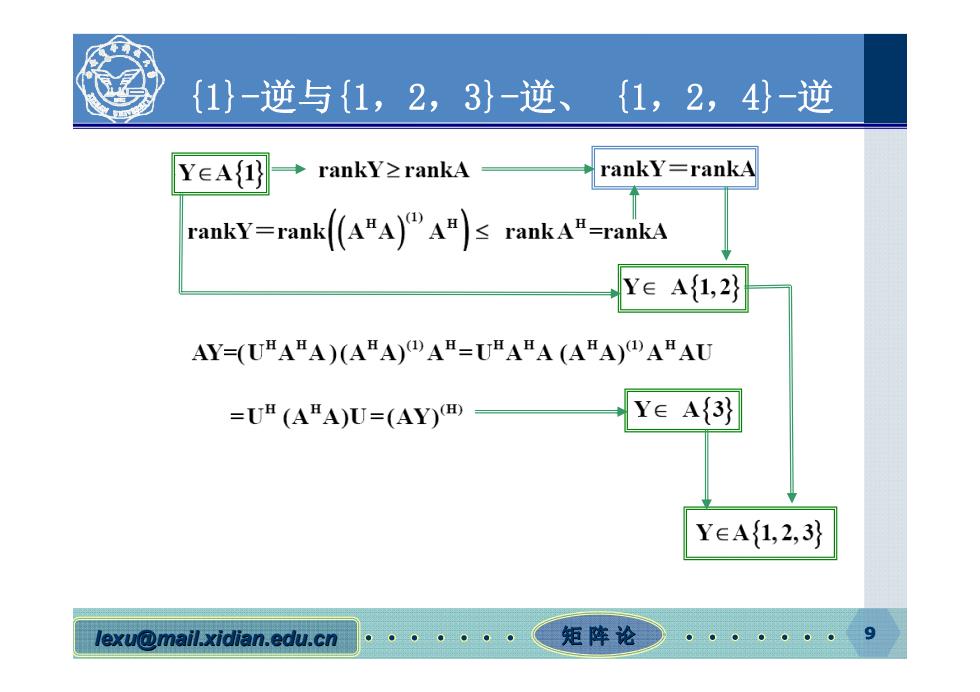
{1}-逆与{1,2,3}-逆、{1,2,4}-逆 YeA{→rankY≥rankA rankY=rankA ranky=rank (A"A)An)s rankA#-rankA Ye Af1,2) AY=(UHAHA)(AHA)DAH-UHABA (AHA)DAHAU =UH (AHA)U=(AY)HD) Y∈A{3} Y∈A{1,2,3} lexu@mail.xidian.edu.cn 矩阵论
9 lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 {1}-逆与{1,2,3}-逆、 {1,2,4}-逆
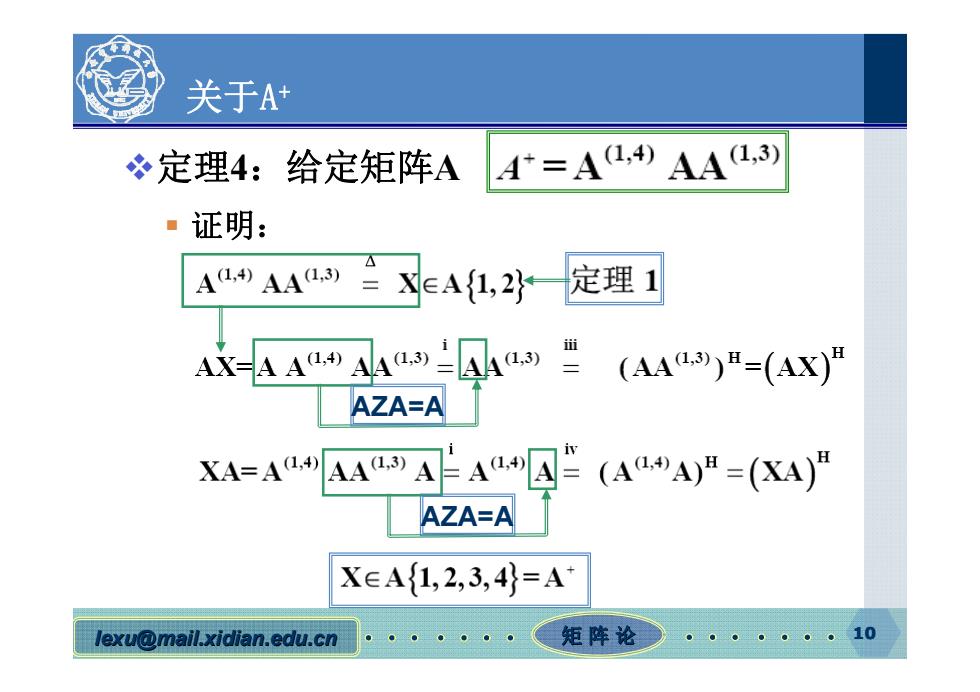
关于A 定理4:给定矩阵A A=A1,)A4L,3 ·证明: A()AA(3)XEA1,2 定理1 Ax=AA()AA(3)) (AA)(Ax) AZA=A XA=AAA AA(AA)"=(KA)" AZA=A X∈A{1,2,3,4}=A lexu@mail.xidian.edu.cn 矩阵论 10
10 lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 10 关于A+ 定理4:给定矩阵A 证明: AZA=A AZA=A