
前 言 有限单元法(Finite Element Method,简称FEM)起源于20世纪40年代至50 年代发展起来的杆系结构矩阵位移法。1956年,Turner等人将这一思想加以推 广,用来求解弹性力学平面问题。1960年,C1ough把这种解决弹性力学问题的 方法命名为“有限单元法”。此后,有限单元法获得迅速发展,逐渐趋于成熟,并 以其理论基础坚实、通用性和实用性极强等突出优点,被公认为最有效的数值方 法。目前,它已成为科学探索的有力工具:计算机辅助设计(CD)和计算机辅助 制造(CAM)的基本组成部分:而且被普遍列为工程力学、结构工程、机械工程、岩 土工程等专业的研究生学位课程。 从学科发展上看,有限单元法在20世纪70年代初期,原理上已基本成熟 方法也逐步趋于完善。不过,到目前为止,在深化理论基础、构造优质单元、扩展 应用范围、提高计算效率与精度等方面仍有发展的余地。特别是对于复杂系统 行为的过程模拟或仿真计算,有限单元法仍面临巨大挑战,例如空间飞行系统响 应的模拟、核反应堆在事故工况下响应的模拟、多场耦合作用分析等。在各种复 杂问题中,有些实质性的东西(例如本构方程)并不属于有限单元法的范围,但其 发展仍需有限元技术的提高与适时参与。 从应用技术上看,到目前为止,己开发出很多商业化的有限元分析软件。 般结构分析问题均可采取通用程序或专用程序求解,不必花费过多精力和时间 另编计算程序。即使如此,为了合理地使用或开发通用程序、准备数据以及恰当 地分析计算结果,必须对有限单元法的基本原理与方法有相当程度的理解,否 则,现成的有限元程序就只能是一个黑箱,使用者将面临很多困难的选择而处于 非常不利的地位。 从本质上讲,有限单元法是求解微分方程的一种近似方法,因此不仅能成功 地处理结构分析中的各种复杂问题,而且还被有效地用于求解热传导、流体力学 以及电磁场等领域的计算问题。本书以结构有限元分析为主,同时介绍与结构 分析有关的热传导问题以及流体与固体相互作用问题。 编写本书的意图是全面而系统地阐述有限单元法的概念、原理和方法,目的 在于使读者能够清晰地表达各种结构分析理论,深刻地理解有限单元法的数学
前 言 有限单元法(FiniteElementMethod,简称FEM)起源于20世纪40年代至50 年代发展起来的杆系结构矩阵位移法。1956年,Turner等人将这一思想加以推 广,用来求解弹性力学平面问题。1960年,Clough把这种解决弹性力学问题的 方法命名为“有限单元法”。此后,有限单元法获得迅速发展,逐渐趋于成熟,并 以其理论基础坚实、通用性和实用性极强等突出优点,被公认为最有效的数值方 法。目前,它已成为科学探索的有力工具;计算机辅助设计(CAD)和计算机辅助 制造(CAM)的基本组成部分;而且被普遍列为工程力学、结构工程、机械工程、岩 土工程等专业的研究生学位课程。 从学科发展上看,有限单元法在20世纪70年代初期,原理上已基本成熟, 方法也逐步趋于完善。不过,到目前为止,在深化理论基础、构造优质单元、扩展 应用范围、提高计算效率与精度等方面仍有发展的余地。特别是对于复杂系统 行为的过程模拟或仿真计算,有限单元法仍面临巨大挑战,例如空间飞行系统响 应的模拟、核反应堆在事故工况下响应的模拟、多场耦合作用分析等。在各种复 杂问题中,有些实质性的东西(例如本构方程)并不属于有限单元法的范围,但其 发展仍需有限元技术的提高与适时参与。 从应用技术上看,到目前为止,已开发出很多商业化的有限元分析软件。一 般结构分析问题均可采取通用程序或专用程序求解,不必花费过多精力和时间 另编计算程序。即使如此,为了合理地使用或开发通用程序、准备数据以及恰当 地分析计算结果,必须对有限单元法的基本原理与方法有相当程度的理解,否 则,现成的有限元程序就只能是一个黑箱,使用者将面临很多困难的选择而处于 非常不利的地位。 从本质上讲,有限单元法是求解微分方程的一种近似方法,因此不仅能成功 地处理结构分析中的各种复杂问题,而且还被有效地用于求解热传导、流体力学 以及电磁场等领域的计算问题。本书以结构有限元分析为主,同时介绍与结构 分析有关的热传导问题以及流体与固体相互作用问题。 编写本书的意图是全面而系统地阐述有限单元法的概念、原理和方法,目的 在于使读者能够清晰地表达各种结构分析理论,深刻地理解有限单元法的数学

有限单元法 力学基础,正确地构造单元并建立有限元公式,比较全面地掌握各种单元的性 能,从而能够有效地利用现有成果和程序进行结构分析,并为改进现有分析理 论、方法和计算程序(例如将新型单元或材料模型接入通用程序)打下坚实的基 础。 本书旨在为两方面的读者提供服务。其一是作为工程力学、结构工程、机械 工程、道路与桥梁工程、岩土工程等专业的研究生教材:其二是作为科技人员和 教师的参考书。作为硕士研究生教材时,建议授课内容(根据课时的多少)从前 14章中选取,难度较大的第15章和第16章可作为研究生继续学习的内容。第 17章简要介绍了在吸收有限元技术的基础上发展起来的边界单元法、有限条 法、有限元线法、无网格法,它有助于读者纵向地了解各种方法的特点,以便必要 时做出合适的选择。 本书编写过程中参考了大量文献资料,在此向他们表示衷心感谢。同时恳 请读者对本书提出批评指正。 编者 2004年10月
力学基础,正确地构造单元并建立有限元公式,比较全面地掌握各种单元的性 能,从而能够有效地利用现有成果和程序进行结构分析,并为改进现有分析理 论、方法和计算程序(例如将新型单元或材料模型接入通用程序)打下坚实的基 础。 本书旨在为两方面的读者提供服务。其一是作为工程力学、结构工程、机械 工程、道路与桥梁工程、岩土工程等专业的研究生教材;其二是作为科技人员和 教师的参考书。作为硕士研究生教材时,建议授课内容(根据课时的多少)从前 14章中选取,难度较大的第15章和第16章可作为研究生继续学习的内容。第 17章简要介绍了在吸收有限元技术的基础上发展起来的边界单元法、有限条 法、有限元线法、无网格法,它有助于读者纵向地了解各种方法的特点,以便必要 时做出合适的选择。 本书编写过程中参考了大量文献资料,在此向他们表示衷心感谢。同时恳 请读者对本书提出批评指正。 编 者 2004年10月 2 有限单元法

录 主要符号 第1章有限单元法基本程式…(1) 1.1弹性力学平面问题… 0) 1.2结构离散… 1.3单元分析… ① 1.4整体分析…自2) 1.5数值求解… 16) 1.6结语…… (19) 习题… 19) 第2章有限单元法基本原理… 21) 2.1微分方程提法… 21) 2.2泛函变分提法…(26) 23位移有限单元法… 33) 2.4应力有限单元法… 37) 2.5结语… (40) 习题…… … 41) 第3章平面问题… 42) 3.1单元构造原则与方法… 42) 3.2矩形单元 45) 3.3高次三角形单元 (49) 3.4T6单元计算 (54 3.5结语… 57) 习题… 57) 第4章空间问题… 58) 4.1环状单元 … (58) 4.2线性四面体单元…。 (63) 4.3高次四面体单元… (68) 4.4结语… (69) 习 题 (70) 第5章等参单元…(1) 5.1等参单元的基本思想…(1)
目 录 主要符号 第1章 有限单元法基本程式 (1)………………………………………………… 11 弹性力学平面问题 (1)…………………………………………………… 12 结构离散 (4)……………………………………………………………… 13 单元分析 (5)……………………………………………………………… 14 整体分析 (12)……………………………………………………………… 15 数值求解 (16)……………………………………………………………… 16 结语 (19)…………………………………………………………………… 习 题 (19)…………………………………………………………………… 第2章 有限单元法基本原理 (21)……………………………………………… 21 微分方程提法 (21)………………………………………………………… 22 泛函变分提法 (26)………………………………………………………… 23 位移有限单元法 (33)……………………………………………………… 24 应力有限单元法 (37)……………………………………………………… 25 结语 (40)…………………………………………………………………… 习 题 (41)…………………………………………………………………… 第3章 平面问题 (42)…………………………………………………………… 31 单元构造原则与方法 (42)………………………………………………… 32 矩形单元 (45)……………………………………………………………… 33 高次三角形单元 (49)……………………………………………………… 34 T6单元计算 (54)………………………………………………………… 35 结语 (57)…………………………………………………………………… 习 题 (57)…………………………………………………………………… 第4章 空间问题 (58)…………………………………………………………… 41 环状单元 (58)……………………………………………………………… 42 线性四面体单元 (63)……………………………………………………… 43 高次四面体单元 (68)……………………………………………………… 44 结语 (69)…………………………………………………………………… 习 题 (70)…………………………………………………………………… 第5章 等参单元 (71)…………………………………………………………… 51 等参单元的基本思想 (71)…………………………………………………

2 有限单元法 5.2平面四边形等参单元 (74 5.3空间六面体等参单元 (79 5.4高次三角形等参单元… 84) 5.5高次四面体等参单元… 85) 5.6数值积分 (86) 5.7结语… (90) 习 题 (91) 第6章杆系结构 (92) 6.1工程梁单元… (92) 6.2剪切梁单元… (101) 6.3通用梁单元… (106) 6.4空间梁单元… 109) 6.5结语 (112) 习 题… (113) 第7章平板结构… (114) 7.1薄板单元 114) 7.2厚板单元 (126) 7.3DKT单元 (130) 7.4通用板单元 (133) 7.5 结语… 。。。。。。 (134) 习 题 (134 第8章壳体结构 (136 8.1平板型壳单元 136 8.2曲面型壳单元 (144 8.3退化型壳单元 (150 8.4结语… (157) 习 题… (157) 第9章若干实际考虑… (158) 9.1单元与网格 (158) 9.2自由度减缩 (159) 9.3结果的处理… (162) 9,4自适应分析… (166) 9.5单元的连接 (170) 96初应变和初应力… (173) 9.7复杂结构材料…(174)
52 平面四边形等参单元 (74)………………………………………………… 53 空间六面体等参单元 (79)………………………………………………… 54 高次三角形等参单元 (84)………………………………………………… 55 高次四面体等参单元 (85)………………………………………………… 56 数值积分 (86)……………………………………………………………… 57 结语 (90)…………………………………………………………………… 习 题 (91)…………………………………………………………………… 第6章 杆系结构 (92)…………………………………………………………… 61 工程梁单元 (92)…………………………………………………………… 62 剪切梁单元 (101)………………………………………………………… 63 通用梁单元 (106)………………………………………………………… 64 空间梁单元 (109)………………………………………………………… 65 结语 (112)………………………………………………………………… 习 题 (113)…………………………………………………………………… 第7章 平板结构 (114)…………………………………………………………… 71 薄板单元 (114)…………………………………………………………… 72 厚板单元 (126)…………………………………………………………… 73 DKT单元 (130)…………………………………………………………… 74 通用板单元 (133)………………………………………………………… 75 结语 (134)………………………………………………………………… 习 题 (134)…………………………………………………………………… 第8章 壳体结构 (136)…………………………………………………………… 81 平板型壳单元 (136)……………………………………………………… 82 曲面型壳单元 (144)……………………………………………………… 83 退化型壳单元 (150)……………………………………………………… 84 结语 (157)………………………………………………………………… 习 题 (157)…………………………………………………………………… 第9章 若干实际考虑 (158)……………………………………………………… 91 单元与网格 (158)………………………………………………………… 92 自由度减缩 (159)………………………………………………………… 93 结果的处理 (162)………………………………………………………… 94 自适应分析 (166)………………………………………………………… 95 单元的连接 (170)………………………………………………………… 96 初应变和初应力 (173)…………………………………………………… 97 复杂结构材料 (174)……………………………………………………… 2 有限单元法

目 9.8结语 (176 习 题… (176 第10章动力分析 … (177 10.1动力有限元方程 (177 10.2结构固有特性 (182 10.3结构动力响应 (184) 10.4解的稳定性… (190) 10.5结语… (192) 习 题… (192) 第11章多场问题 (194) 11.1热传导与变温应力… (194) 11.2流体与结构相互作用 (200) 11.3结语… 204) 习 题… 204) 第12章有限元原理进阶与单元构造 205) 12.1修正泛函及其构造方法… (205) 122广义变分原理与混合单元… (207) 12.3修正变分原理与杂交单元 (213) 12.4加权余量法与单元构造… (221) 12.5小片试验与非协调元 (225) 12.6结语 232) 习 题… (232) 第13章非线性方程求解 234 13.1迭代法, 234 13.2增量法 242 13.3若干实际考虑 244 13.4结语… 247 习 题 247) 第14章材料非线性问题 (248) 14.1材料本构方程… 248) 14.2弹塑性有限元方程 (263) 14.3流变有限元方程… 265) 14.4 若干实际考虑… 267) 14.5结语… 268) 题… 269)
98 结语 (176)………………………………………………………………… 习 题 (176)…………………………………………………………………… 第10章 动力分析 (177)………………………………………………………… 101 动力有限元方程 (177)…………………………………………………… 102 结构固有特性 (182)……………………………………………………… 103 结构动力响应 (184)……………………………………………………… 104 解的稳定性 (190)………………………………………………………… 105 结语 (192)………………………………………………………………… 习 题 (192)…………………………………………………………………… 第11章 多场问题 (194)………………………………………………………… 111 热传导与变温应力 (194)………………………………………………… 112 流体与结构相互作用 (200)……………………………………………… 113 结语 (204)………………………………………………………………… 习 题 (204)…………………………………………………………………… 第12章 有限元原理进阶与单元构造 (205)…………………………………… 121 修正泛函及其构造方法 (205)…………………………………………… 122 广义变分原理与混合单元 (207)………………………………………… 123 修正变分原理与杂交单元 (213)………………………………………… 124 加权余量法与单元构造 (221)…………………………………………… 125 小片试验与非协调元 (225)……………………………………………… 126 结语 (232)………………………………………………………………… 习 题 (232)…………………………………………………………………… 第13章 非线性方程求解 (234)………………………………………………… 131 迭代法 (234)……………………………………………………………… 132 增量法 (242)……………………………………………………………… 133 若干实际考虑 (244)……………………………………………………… 134 结语 (247)………………………………………………………………… 习 题 (247)…………………………………………………………………… 第14章 材料非线性问题 (248)………………………………………………… 141 材料本构方程 (248)……………………………………………………… 142 弹塑性有限元方程 (263)………………………………………………… 143 流变有限元方程 (265)…………………………………………………… 144 若干实际考虑 (267)……………………………………………………… 145 结语 (268)………………………………………………………………… 习 题 (269)…………………………………………………………………… 目 录 3

4 有限单元法 第15章几何非线性问题 270 15.1变形和位移 (270 15.2应变度量… (276) 15.3应力度量… 280) 15.4本构方程… 283) 15.5平衡方程 (286) 15.6微分方程弱形式… 286) 15.7有限元离散方程… 289) 15.8结语 (296) 习 题… 296) 第16章边界非线性问题 298) 16.1接触问题定义 298) 16.2接触分析原理… 303) 16.3接触问题算法… 304) 16.4结语… 308) 习 题… 309) 第17章有限单元法旁系发展 310) 17.1边界单元法 310) 17.2有限条法 314) 17.3有限元线法 319 17.4 无网格法· 322 17.5结语 326 习 题 (326 参考文献 327)
第15章 几何非线性问题 (270)………………………………………………… 151 变形和位移 (270)………………………………………………………… 152 应变度量 (276)…………………………………………………………… 153 应力度量 (280)…………………………………………………………… 154 本构方程 (283)…………………………………………………………… 155 平衡方程 (286)…………………………………………………………… 156 微分方程弱形式 (286)…………………………………………………… 157 有限元离散方程 (289)…………………………………………………… 158 结语 (296)………………………………………………………………… 习 题 (296)…………………………………………………………………… 第16章 边界非线性问题 (298)………………………………………………… 161 接触问题定义 (298)……………………………………………………… 162 接触分析原理 (303)……………………………………………………… 163 接触问题算法 (304)……………………………………………………… 164 结语 (308)………………………………………………………………… 习 题 (309)…………………………………………………………………… 第17章 有限单元法旁系发展 (310)…………………………………………… 171 边界单元法 (310)………………………………………………………… 172 有限条法 (314)…………………………………………………………… 173 有限元线法 (319)………………………………………………………… 174 无网格法 (322)…………………………………………………………… 175 结语 (326)………………………………………………………………… 习 题 (326)…………………………………………………………………… 参考文献 (327)……………………………………………………………………… 4 有限单元法

主要符号 主要符号 单元面积 A 平面问题或板弯曲问题中的单元面积域 a 单元节点位移向量 整体节点位移向量 B,Bi 单元应变矩阵及其子矩阵 Bb Bbi 板单元弯曲应变矩阵及其子矩阵 B Bsi 板单元剪切应变矩阵及其子矩阵 C 阻尼矩阵或柔度矩阵 弹性矩阵 弹性模量 体力向量 G 剪切模量 J,J Jacobi矩阵及其行列式 K,K 单元刚度矩阵,整体刚度矩阵 Li 三角形单元的面积坐标 M 弯矩 M 质量矩阵或薄板弯曲中力矩组成的广义应力向量 M,My Mo 板弯曲问题中垂直x轴和y轴的截面上单位长度 的弯矩及扭矩 N,Ni 单元形函数矩阵,节点;的形函数 P,P 整体荷载向量,单元等效节点荷载向量 面力向量 转换矩阵 单元厚度 单元位移向量 u,v,w 位移向量的分量,表示x,y,之方向的位移 应变向量 6 应力向量 方向余弦矩阵
主 要 符 号 A 单元面积 Ae 平面问题或板弯曲问题中的单元面积域 ae 单元节点位移向量 a 整体节点位移向量 B,Bi 单元应变矩阵及其子矩阵 Bb,Bbi 板单元弯曲应变矩阵及其子矩阵 Bs,Bsi 板单元剪切应变矩阵及其子矩阵 C 阻尼矩阵或柔度矩阵 D 弹性矩阵 E 弹性模量 f 体力向量 G 剪切模量 J,J Jacobi矩阵及其行列式 Ke,K 单元刚度矩阵,整体刚度矩阵 Li 三角形单元的面积坐标 M 弯矩 M 质量矩阵或薄板弯曲中力矩组成的广义应力向量 Mx,My,Mxy 板弯曲问题中垂直x轴和y轴的截面上单位长度 的弯矩及扭矩 N,Ni 单元形函数矩阵,节点i的形函数 P,Pe 整体荷载向量,单元等效节点荷载向量 p 面力向量 T 转换矩阵 t 单元厚度 u 单元位移向量 u,v,w 位移向量的分量,表示x,y,z方向的位移 ε 应变向量 σ 应力向量 方向余弦矩阵 主要符号 1

2 有限单元法 0,0a,0 梁、板、壳法线转角 5,7,5 单元局部坐标或等参坐标 Ⅱc,Ⅱm 余能泛函及修正余能泛函 Lp,Ⅱme 势能泛函及修正势能泛函 2,T 求解域及其边界
θ , θxi , θyi 梁、板、壳法线转角 ξ , η , ζ 单元局部坐标或等参坐标 Πc , Π m c 余能泛函及修正余能泛函 Πp , Π m p 势能泛函及修正势能泛函 Ω , Γ 求解域及其边界 2 有限单元法

第1章 有限单元法基本程式 有限单元法(Finite Element Method,简称FEMD是一种求解微分方程的近 似方法,起点自然是针对物理或工程问题建立起来的微分方程,包括控制方程和 边界条件:而有限元分析程式早己标准化,典型步骤包括结构或区域离散、单元 分析、整体分析和数值求解。 本章以弹性力学平面问题为例,阐述有限单元法的基本概念与程式。采用 有限单元法求解平面问题不仅简单,而且具有典型性。掌握了平面问题的有限 元分析方法,就可以很容易地推广到其他问题中去。 1.1弹性力学平面问题 1.1.1基本概念 平面问题是指这样一些问题,其结构尺寸及荷载分布沿某个方向(通常取为 之轴)不变,且具有特殊的边界条件。这样,结构内部的应力和应变就与之坐标 无关,而只是x,y坐标的函数。平面问题分为两种,即平面应力问题和平面应 变问题。 1)平面应力问题 如果在结构内部只存在xy平面内的三个应力分量。,o,c,而另外三个 应力分量=xa=x=0,则称为平面应力问题。例如,只承受纵向面内荷载 的薄板就可近似地视为这种问题(图1.1):由于板很薄,故可认为应力和应变 与之坐标无关。再注意到平板两面上的a,=x=t=0,便可近似地认为这些 应力分量在板内也为零。对于各向同性线性弹性介质,根据广义Hooke定律, 平面应力问题中的Yz和Y,显然为零,而e:由下式确定 ,=-(+) 1.1) 其中,E为弹性模量:v为泊松比
第 1章 有限单元法基本程式 有限单元法(FiniteElementMethod,简称FEM)是一种求解微分方程的近 似方法,起点自然是针对物理或工程问题建立起来的微分方程,包括控制方程和 边界条件;而有限元分析程式早已标准化,典型步骤包括结构或区域离散、单元 分析、整体分析和数值求解。 本章以弹性力学平面问题为例,阐述有限单元法的基本概念与程式。采用 有限单元法求解平面问题不仅简单,而且具有典型性。掌握了平面问题的有限 元分析方法,就可以很容易地推广到其他问题中去。 11 弹性力学平面问题 111 基本概念 平面问题是指这样一些问题,其结构尺寸及荷载分布沿某个方向(通常取为 z轴)不变,且具有特殊的边界条件。这样,结构内部的应力和应变就与z坐标 无关,而只是x,y坐标的函数。平面问题分为两种,即平面应力问题和平面应 变问题。 (1)平面应力问题 如果在结构内部只存在xy平面内的三个应力分量σx,σy,τxy,而另外三个 应力分量σz=τzx=τzy=0,则称为平面应力问题。例如,只承受纵向面内荷载 的薄板就可近似地视为这种问题(图11a):由于板很薄,故可认为应力和应变 与z坐标无关。再注意到平板两面上的σz=τzx=τzy=0,便可近似地认为这些 应力分量在板内也为零。对于各向同性线性弹性介质,根据广义 Hooke定律, 平面应力问题中的γzx和γzy显然为零,而εz由下式确定 εz=-ν E( ) σx+σy (11) 其中,E 为弹性模量;ν为泊松比
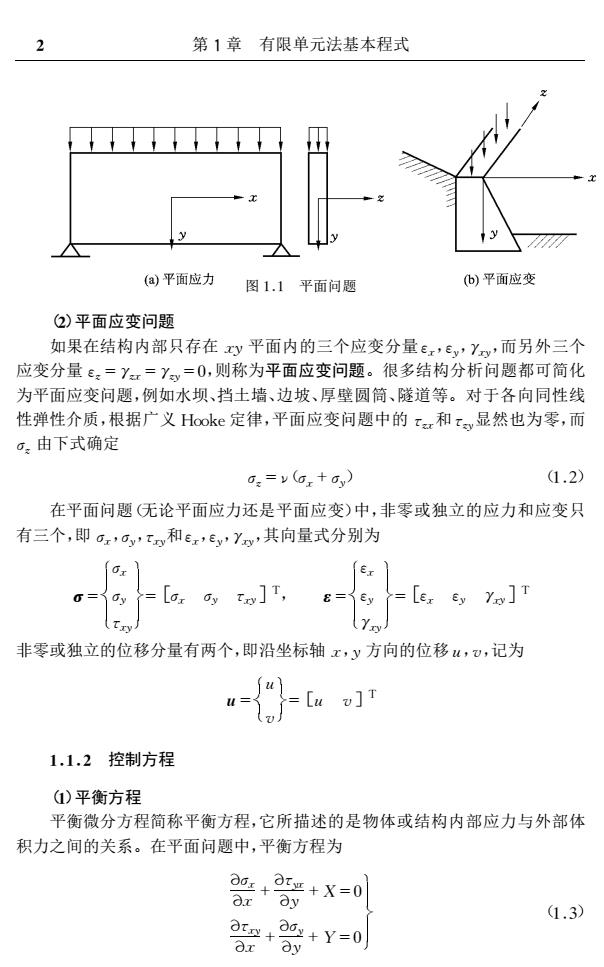
第1章有限单元法基本程式 (a)平面应力 图1.1平面问题 )平面应变 )平面应变问题 如果在结构内部只存在xy平面内的三个应变分量e,Ev,Y,而另外三个 应变分量:=Yx=Y=0,则称为平面应变问题。很多结构分析问题都可简化 为平面应变问题,例如水坝、挡土墙、边坡、厚壁圆筒、隧道等。对于各向同性线 性弹性介质,根据广义Hooke定律,平面应变问题中的x和x,显然也为零,而 o:由下式确定 as=y (a,+ay) 1.2) 在平面问题无论平面应力还是平面应变)中,非零或独立的应力和应变只 有三个,即a,oy,x和ex,y,Y,其向量式分别为 Er ay to]T, E=y =Ler Ey]T 非零或独立的位移分量有两个,即沿坐标轴x,y方向的位移,o,记为 u =[u v]T 1.1.2控制方程 ①)平衡方程 平衡微分方程简称平衡方程,它所描述的是物体或结构内部应力与外部体 积力之间的关系。在平面问题中,平衡方程为 ++X=0】 .3) 2+0+y-0
图11 平面问题 (2)平面应变问题 如果在结构内部只存在xy平面内的三个应变分量εx,εy,γxy,而另外三个 应变分量εz=γzx=γzy=0,则称为平面应变问题。很多结构分析问题都可简化 为平面应变问题,例如水坝、挡土墙、边坡、厚壁圆筒、隧道等。对于各向同性线 性弹性介质,根据广义 Hooke定律,平面应变问题中的τzx和τzy显然也为零,而 σz由下式确定 σz=ν(σx+σy) (12) 在平面问题(无论平面应力还是平面应变)中,非零或独立的应力和应变只 有三个,即σx,σy,τxy和εx,εy,γxy,其向量式分别为 σ= σx σy τx 烅 烄 烆 烍 烌 y烎 =[ ] σx σy τxy T, ε= εx εy γx 烅 烄 烆 烍 烌 y烎 =[ ] εx εy γxy T 非零或独立的位移分量有两个,即沿坐标轴x,y方向的位移u,v,记为 u= u 烅 烄 烆 烍 烌 v烎 =[ ] u v T 112 控制方程 (1)平衡方程 平衡微分方程简称平衡方程,它所描述的是物体或结构内部应力与外部体 积力之间的关系。在平面问题中,平衡方程为 σx x+ τyx y +X=0 τxy x + σy y +Y 烍 烌 =0烎 (13) 2 第1章 有限单元法基本程式