
西安毛子科技大枣三XIDIANUNIVERSITY$4.6初等矩阵初等矩阵二、等价矩阵三、用初等变换求矩阵的逆
一、初等矩阵 二、等价矩阵 三、用初等变换求矩阵的逆

西安毛子科技大学XIDIAN UNIVERSITY一、初等矩阵定义由单位矩阵E经过一次初等变换得到的矩阵,称为初等矩阵三种初等变换对应着三种初等方阵:1.对调两行或两列:2.以数k0 乘某行或某列;3.以数k乘某行(列)加到另一行(列)上去
由单位矩阵 E 经过一次初等变换得到 的矩阵,称为初等矩阵. 定义 一、初等矩阵 三种初等变换对应着三种初等方阵: 以数 乘某行(列)加到另一行(列)上去. 以数 乘某行或某列; 对调两行或两列; k k 3. 2. 0 1

西安毛子科技大枣三XIDIANUNIVERSITY1、对调两行或两列对调E中第i,i两行,即(r;台r),得初等方阵←第i行P(i,j) =←第i行(换法矩阵)
对调 E 中第 i, j 两行,即(ri rj ),得初等方阵 1、对调两行或两列 1 1 0 1 1 ( , ) 1 1 0 1 1 P i j = 第 i 行 第 j 行 (换法矩阵)
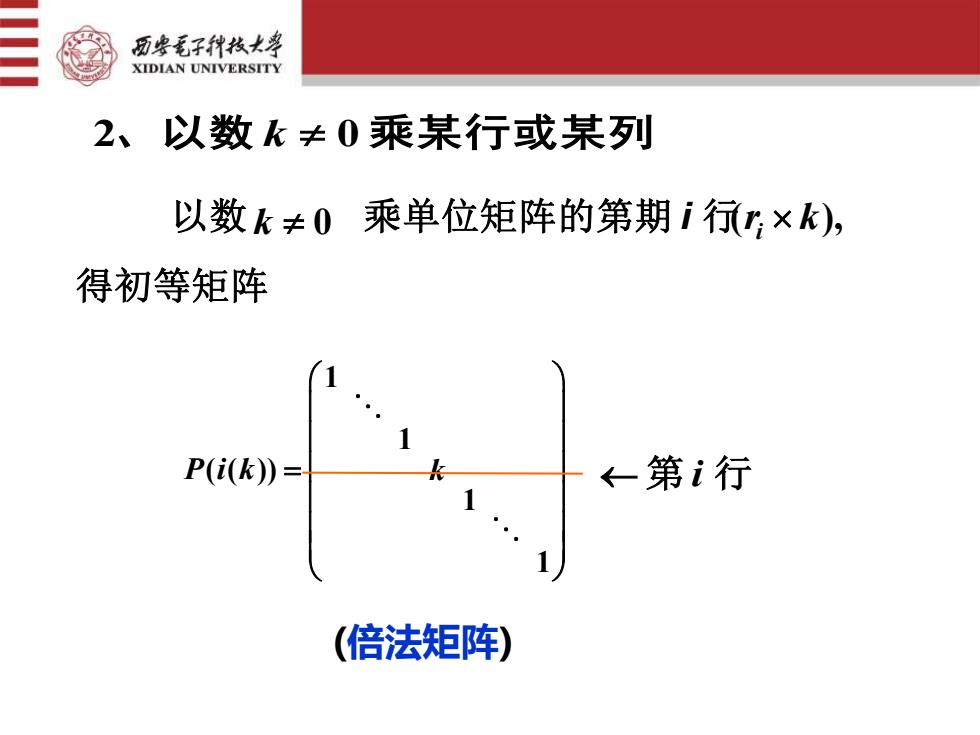
西安毛子科技大学XIDIANUNIVERSITY2、以数k≠0乘某行或某列以数k±0乘单位矩阵的第期i行(r,×k),得初等矩阵P(i(k) =←第i行(倍法矩阵)
2、以数 k 0 乘某行或某列 1 1 ( ( )) 1 1 P i k k = 第 i 行 (倍法矩阵) 以数 乘单位矩阵的第期 i 行 得初等矩阵 ( ), i k 0 r k

西安毛子科技大学三XIDIANUNIVERSITY3、以数k± 0乘某行(列)加到另一行(列)上去以k乘E的第i行加到第i行上(r;+kr,)[或以k乘E的第i列加到第j列上(c;+kc,),←第行P(i, j(k) =←第行1(消法矩阵)
3、以数k 0乘某行(列)加到另一行(列)上 去 或以 乘 的第 列加到第 列上 , 以 乘 的第 行加到第 行上 [ ( ) ( ) j i i j k E i j c kc k E j i r kr + + 1 1 ( , ( )) 1 1 k P i j k = 第i行 第j行 (消法矩阵)

西安毛子科技大学XIDIANUNIVERSITY初等矩阵的性质1初等矩阵皆可逆,且其逆仍为初等矩阵P(i,j)-1 = P(i, j),P(i(k)-1 = P(i()P(i,j(k))-1 = P(i,j(-k))
1 初等矩阵皆可逆,且 其逆仍为初等矩阵. 初等矩阵的性质 1 P i j P i j ( , ) ( , ), − = 1 1 P i k P i ( ( )) ( ( )), k − = 1 P i j k P i j k ( , ( )) ( , ( )). − = −

西安毛子科技大学三XIDIAN UNIVERSITY2 引理 对任一矩阵A作一初等行(列)变换相当于对A 左(右)乘一个相应的初等矩阵。P(i,j)A:对换A的i,j两行:AP(i,j):对换A的i,j两列P(i(k)A :用非零数k乘A 的第i 列;AP(i(k):用非零数k 乘 A 的第i 列P(i,j(k)A:A的第j行乘以k加到第i行;AP(i,j(k)) :A 的第i列乘以k加到第j列
2 引理 对任一矩阵 A 作一初等行(列)变换相当于 对 A 左(右)乘一个相应的初等矩阵. P i j A ( , ) : 对换 A 的 i j , 两行; AP i j ( , ) : 对换 A 的 i j , 两列. P i k A ( ( )) :用非零数 k 乘 A 的第 i 列; AP i k ( ( )) :用非零数 k 乘 A 的第 i 列. : 的第 行乘以 加到第 行 ; P i j k A ( , ( )) A j k i AP i j k ( , ( )) :A 的第 i 列乘以 k加到第j 列.

西安毛子科技大学XIDIANUNIVERSIT二、等价矩阵定义若矩阵B可由A经过一系列初等变换得到则称A与B等价的.(也称A与B相抵)注:D矩阵的等价关系具有:反射性、对称性、传递性2等价矩阵的秩相等福
若矩阵B可由A经过一系列初等变换得到, 则称A与B等价的.(也称A与B相抵) ① 矩阵的等价关系具有: 反射性、对称性、传递性. ② 等价矩阵的秩相等. 二、等价矩阵 定义 注:

西要毛子科技大学XIDIANUNIVERSITY矩阵等价的有关结论1)定理5任一s×n矩阵A都与一形式为00的矩阵等价,称之为A的标准形,且主对角线上1的个数 r等于R(A)(1的个数可以是零)
1) 定理5 任一 s n 矩阵 A 都与一形式为 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 Er 矩阵等价的有关结论 的矩阵等价,称之为 A 的标准形, 且主对角线上1 的个数 r 等于R(A)(1的个数可以是零)

西要毛子律技大學XIDIANUNIVERSITY2)矩阵A、B等价<>存在初等矩阵 P,P2,,P,,Q,Q2,…,Q,使B= PP....P,AQQ....Q.3)n级方阵A可逆<>A的标准形为单位矩阵EA与单位矩阵E等价4)n 级方阵A可逆<>A能表成一些初等矩阵的积,即 A=Q,,Q,定理6
2) 矩阵A、B等价 1 2 1 2 . B P P P AQ Q Q = s t 存在初等矩阵 1 2 1 2 , , , , , , , , P P P Q Q Q s t 使 3) n 级方阵A可逆 A的标准形为单位矩阵E. A与单位矩阵E等价. 1 2 . 即 A Q Q Q = t 4) n 级方阵A可逆 A能表成一些初等矩阵的积, 定理6