西安电子科技大学：《高等代数》课程PPT教学课件（讲稿）第四章 矩阵 4.5 矩阵的分块

西安毛子科技大学XIDIAN UNIVERSITY$4.5矩阵的分块、分块矩阵的概念二、分块矩阵的运算三、准对角矩阵

一、分块矩阵的概念 二、分块矩阵的运算 三、准对角矩阵

西安毛子科技大学一XIDIAN UNIVERSITY一、分块矩阵的概念定义 设A是一个矩阵，在A的行或列之间加上一些线，把这个矩阵分成若干小块．用这种方法被分成若于小块的矩阵叫做一个分块矩阵每一个分块的方法叫做A一种分法

一、分块矩阵的概念 定义 设A是一个矩阵，在A的行或列之间加上 一些线，把这个矩阵分成若干小块．用这种 方法被分成若干小块的矩阵叫做一个分块矩阵． 每一个分块的方法叫做A一种分法．

西安毛子科技大学XIDIAN UNIVERSITY特殊分法设矩阵 A=(aj)sn"(A)A按行分块 A=其中 A, =(ai1,ai2,"",ain),:i =1,2,...,s.A.aiani按列分块A=（A,A,,A)，其中A,=...j=1,2,...,nari)

特殊分法 按行分块 1 2 , s A A A A     =         其中 1 2 ( , , , ), A a a a i i i in = 按列分块 A A A A = ( 1 2 , , , n ) ，其中 1 2 , j j j nj a a A a       =         设矩阵 ( ) , A a = ij s n j n = 1,2, , . i s = 1,2, ,

西安毛子科技大学二XIDIAN UNIVERSITY一、分块矩阵的运算1、加法设A,B是两个 m×n矩阵，对它们用同样的分法分块：B.B.A11A=B.BBA其中子块 A,与 B,为同型矩阵，则A1+ BA+B=+BsIB

          =           = s sr r s sr r B B B B B A A A A A         1 1 1 1 1 1 1 1 , 1、加法 设 A, B 是两个 m n  矩阵，对它们 一、分块矩阵的运算 . 1 1 1 1 1 1 1 1           + + + + + = s s sr sr r r A B A B A B A B A B     用同样的分法分块: 其中子块 Aij 与 Bij 为同型矩阵，则

西安毛子科技大学XIDIAN UNIVERSITY2、数量乘法aeP，则设分块矩阵A=A.1A.(2Au2A2A=2A.12As

2、数量乘法 . 1 1 1 1   = s srr A A A A A          设分块矩阵 11 1 1 , , r s sr A A A P A A      =        则

西要毛子科技大学-XIDIANUNIVERSITY3、乘法把矩阵 A=(aik）mn,B=(bj）nxp分块成B11AlAtBurA=B=Bt1...BrAs1A.其中Ai,A2,A,的列数分别等于Bu,B2,,B的行数,那么(CuCirAB=::CC.其中C,=A,B(i=-l,...,s; j-l,,r)k=l

, , 1 1 1 1 1 1 1 1           =           = t tr r s st t B B B B B A A A A A         1 2 1 2 , , , , , , , 其中A A A B B B i i it j j ij 的列数分别等于 的行数 那么           = s sr r C C C C AB     1 11 1 ( 1, , ; 1, , ). 1 C A B i s j r k j t k i j =  i k =  =  = 其 中 3、乘法 把矩阵 ( ) , ( ) A a B b = = ik m n kj n p   分块成

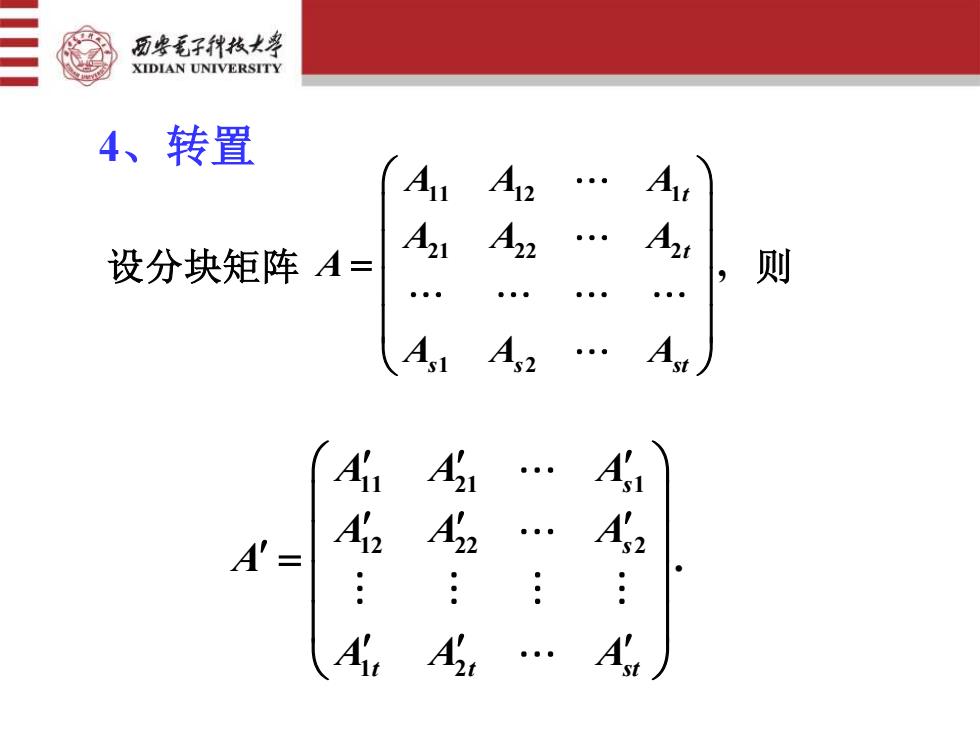
西安毛子科技大学XIDIANUNIVERSIT4、转置A.A12mA223则设分块矩阵 A=AsA.A.SstA'Al1A21s1A2A2A's2:：:A'AfA

11 21 1 12 22 2 1 2 . ss t t st A A A A A A A A A A              =          设分块矩阵 11 12 1 21 22 2 1 2 , tt s s st A A A A A A A A A A       =       则 4、转置

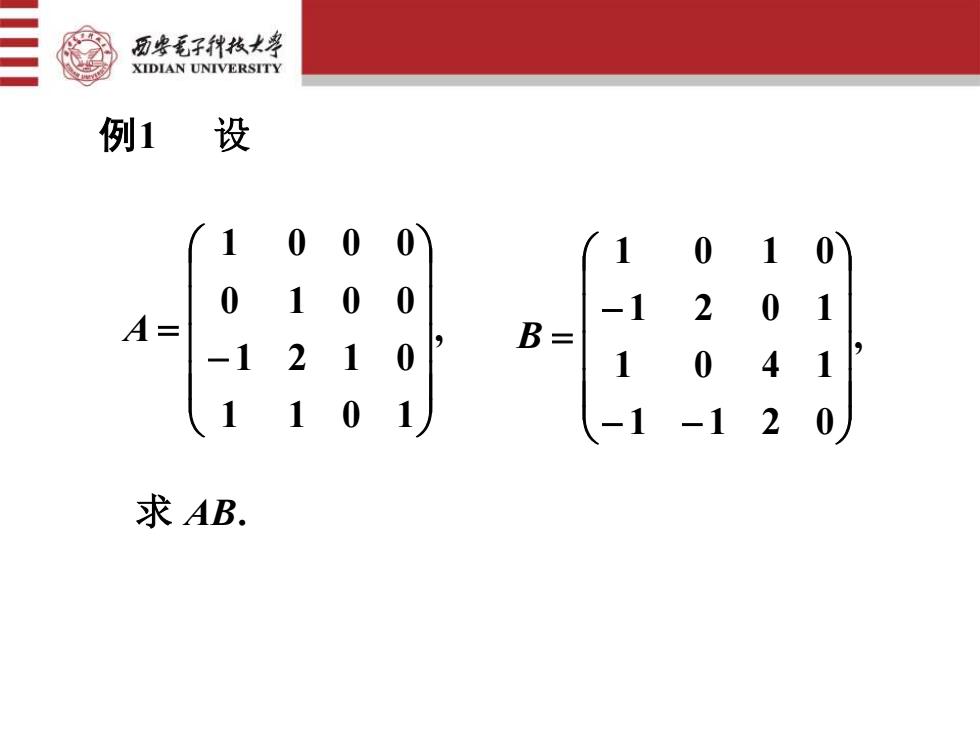
西安毛子科技大学XIDIAN UNIVERSITY设例1 0001001100070-121A=B =2010141111201-1求 AB

例1 设 , 1 1 0 1 1 2 1 0 0 1 0 0 1 0 0 0               − A = , 1 1 2 0 1 0 4 1 1 2 0 1 1 0 1 0               − − − B = 求 AB

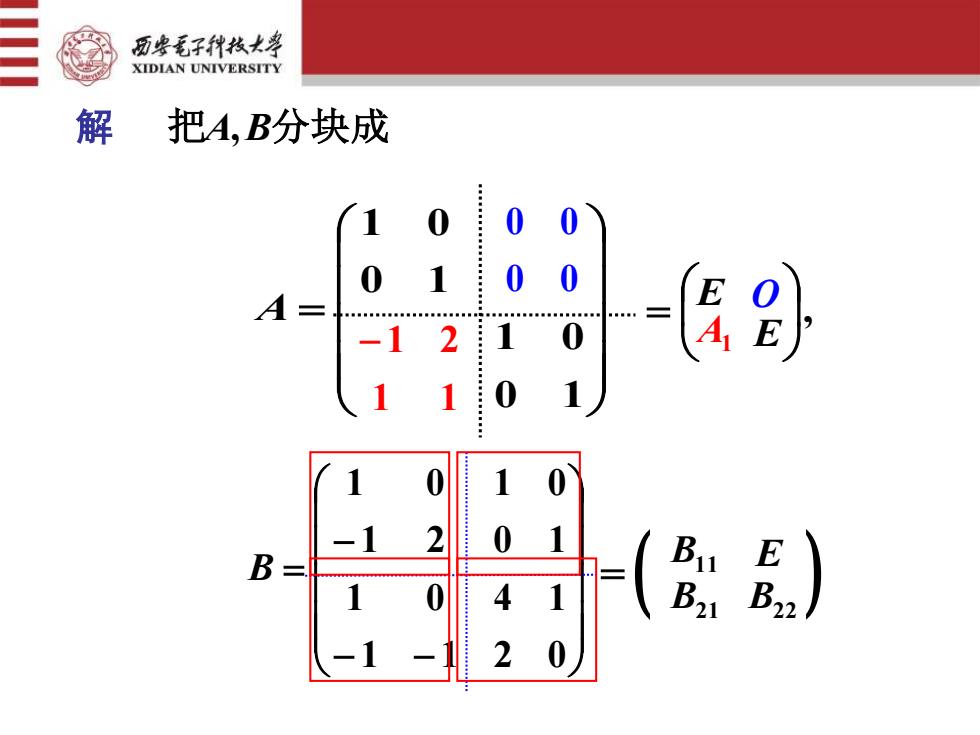
西安毛子律技大枣XIDIANUNIVERSITY解把A,B分块成00102110002BuEB :0B21B224110-12

解 把A,B分块成               = 0 1 1 0 0 1 1 0 A 0 0 0 0 1 1 − 1 2 ,      = E E O A1               − − − = 1 1 2 0 1 0 4 1 1 2 0 1 1 0 1 0 B ( ) = B11 E B21 B22

西安毛子律技大学XIDIANUNIVERSITYE0EBu1则AB :B22 E儿B21AlEBr1A +B,B + B210又 A,Bu + B210S

则    = 21 22 11 1 B B B E A E E O AB . 1 11 21 1 22 11   + + = A B B A B B E 又 A1 B11 + B21   − −  +  −   − = 1 1 1 0 1 2 1 0 1 1 1 2   − −  +  − = 1 1 1 0 0 2 3 4 , 1 1 2 4  −− =    +  − + = 2 0 4 1 1 1 1 2 A1 B22 , 3 1 3 3  =