
UNIVE 矩阵论 主讲教师:徐乐 2014年12月10日星期三
2014年12月10日星期三 矩 阵 论 主讲教师:徐乐

上讲回顾 第16讲Penrose广义逆的性质(四 ·{1}-逆与{1,2,3}-逆、{1,2,4}-逆 ·关于A+ ·广义逆的计算 ·由Hermite标准形求{}-逆 ·由满秩分解求广义逆 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第16讲 Penrose广义逆的性质(II) {1}-逆与{1,2,3}-逆、 {1,2,4}-逆 关于A+ 广义逆的计算 • 由Hermite标准形求{1}-逆 • 由满秩分解求广义逆

上讲回顾 冬引理:对任意矩阵A均有 rank(AHA)=rankA rank(AAH) 定理3:给定矩阵A,则 Y=(AA)AH∈A{1,2,3} Z=AH(AAH)四∈A{1,2,4} 冬定理4:给定矩阵A A=A1)AA13) lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 上讲回顾 引理:对任意矩阵A均有 rank(AHA) = rankA = rank(AAH) 定理3: 给定矩阵A , 则 定理4:给定矩阵A

上讲回顾 定理5:给定矩阵A,则 (1)rank4*=rankA (2)(A)*=A (3)(A)*=(A*)F,(AP)=(A+)A (4)(44)=4(4),(44)*=(4)4 (5) A*=(AA)*A=A(A4) (6)R(A)=R(A),N()=N(AF) lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 上讲回顾 定理5: 给定矩阵A,则

上讲回顾 必推论1若A∈Cm"(列满秩矩阵),则A*=(A#A)~AH A∈Cm(行满秩矩阵),则A*=A(AA) 推论2对非零列向量a,a*=(aa)'a 对非零行向量B,P广=B(BB);,B均为数 Note A,B可逆,则(AB)1=BA1,但一般(.AB)≠BA lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 上讲回顾 推论1 推论2 Note
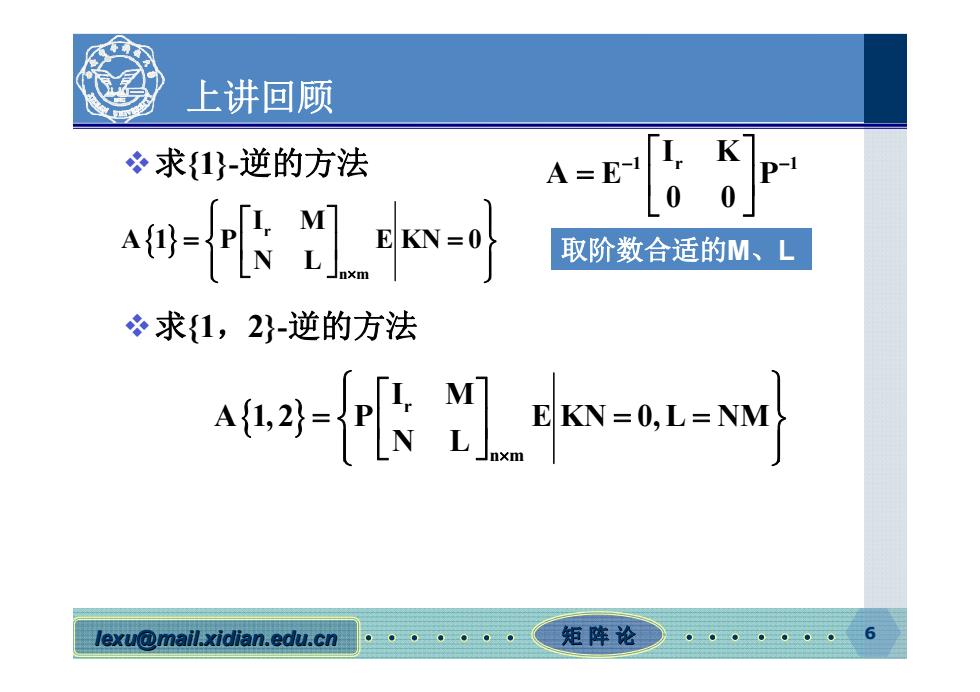
上讲回顾 冬求{1}-逆的方法 A-E -= 取阶数合适的M、L 冬求1,2-逆的方法 -r仆k-u lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 上讲回顾 求{1}-逆的方法 求{1,2}-逆的方法 r n m I M A 1 P E KN 0 N L 取阶数合适的M、L 1 1 r I K AE P 0 0 r n m I M A 1, 2 P E KN 0,L NM N L

上讲回顾 。由满秩分解求广义逆 ·对A进行满秩分解 A=FG,A∈Cmx,F∈Cm,GeC0 ·定理] (1)GOF四∈A{ i=1,2,4 (2)GOFDEA{}i=1,2,3 (3)GF*∈A{1,2,3},G*F0∈A{1,2,4} (4)A*=GF1,3)=G1,+F 5)A*=GF=GGG)FF)FH=GFHAG)F lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 7 上讲回顾 由满秩分解求广义逆 对A进行满秩分解 [定理]

第17讲Penrose广义逆与Moore广义逆 投影矩阵与Moore-Penrose逆 ·投影算子与投影矩阵 ·正交投影算子与正交投影矩阵 ■投影矩阵与广义逆矩阵 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 第17讲 Penrose广义逆与Moore广义逆 投影矩阵与Moore-Penrose逆 投影算子与投影矩阵 正交投影算子与正交投影矩阵 投影矩阵与广义逆矩阵

投影算子与投影矩阵 冬投影 ·设L,M为C的子空间并构成直和L+M=L⊕M=C ·即x∈C",3唯一的y∈L,z∈M使x=y+z ·称y为x沿着M到L的投影 冬定义 ■将任意x∈Cn变为其沿着M到L的投影的变换 称为沿着M到L的投影算子,记为PL,M ·即PMx=y∈L ·投影算子是线性变换,其矩阵称为投影矩阵,仍记为 PLM lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 投影算子与投影矩阵 投影 设L,M为Cn的子空间并构成直和 • 即 • 称 y为x沿着M到L的投影 定义 将任意 x∈Cn 变为其沿着M到L的投影的变换 称为沿着M到L的投影算子,记为PL,M • 即 • 投影算子是线性变换,其矩阵称为投影矩阵,仍记为 PL,M n LML MC
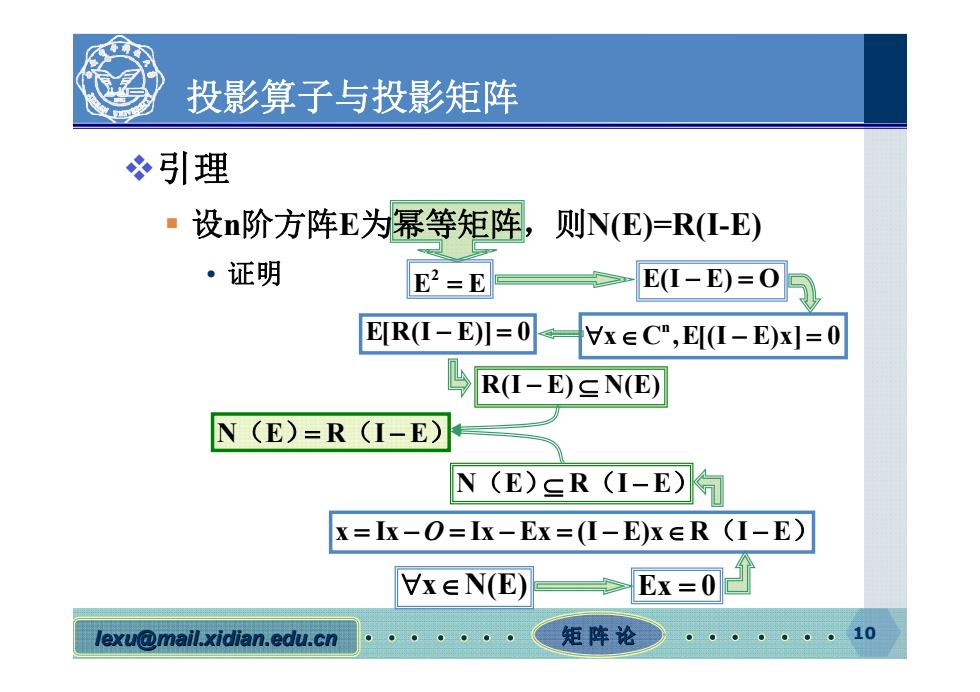
投影算子与投影矩阵 冬引理 ·设n阶方阵E为幂等矩阵, 则NE)=R(I-E) ·证明 E2=E E(I-E)=0 ERI-E)川=0 x∈C",EI-E)x=0 R(I-E)EN(E) N (E)=R (I-E) N(E)SR(I-E)句 x=x-O=Ix-Ex=(I-E)x∈R(I-E) x∈NE) Ex=0 lexu@mail.xidian.edu.cn 矩阵论 10
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 10 投影算子与投影矩阵 引理 设n阶方阵E为幂等矩阵,则N(E)=R(I-E) • 证明 E(I E) O x N(E) Ex 0 NE RIE () ( ) 2 E E E[R(I E)] 0 n x C ,E[(I E)x] 0 R(I E) N(E) NE RIE () ( ) x Ix Ix Ex (I E)x R I E O ( )