西安电子科技大学：《复变函数与场论》课程教学课件（讲义，2017）第22讲 留数在积分中的应用及复习

IT UNIVER 场论与复变函数 主讲：徐乐

场论与复变函数 主讲：徐乐

Review 留数 Res[f(=),-o] 2aee 留数定理 重fe)t=2πi∑ResIf(-),l m的取值可以 k=1 比函数极点的 留数计算 实际级数高， 而并不会影响 规则Ⅱ的有效 ·Rule:若zn为函数f(z)的一级极点，则 性，有时候将m Res[f(z),z0]=lim(z-z0)f(z) 取的比实际级 z→20 数高可以简化 ·Rule I:若z为函数fa)的m级极点，则 留数计算 Res[f(=).-o]=- e-r ·Rule IⅢ：设Pa、(a)在解析，Pa0、Qzo=0、 2'(a)≠0，则 )s P() Res()]=P() 2(). Q'() lexu@mail.xidian.edu.cn F&C

lexu @mail.xidian.edu.cn F & C 2 Review 留数 留数定理 留数计算  Rule I：若 z 0为函数 f ( z) 的一级极点，则  Rule II：若 z 0为函数 f ( z) 的 m 级极点，则  Rule III：设 P ( z ) 、 Q ( z ) 在 z 0解析,P ( z 0) ≠ 0 、 Q ( z 0)=0 、 Q’ ( z 0) ≠ 0, 则 0 1 1 Re [ ( ), ] ( ) 2 C s f z z f z dz c  i     1 ( ) 2 Re [ ( ), ] n k C k f z dz i s f z z      0 Re [ ( ), ] lim( ) ( ) 0 0 z z s fz z z z fz    0 1 0 0 1 1 Re [ ( ), ] lim ( ) ( ) ( 1)! m m m z z d s fz z z z fz m dz           ( ) ( ) ( ) P z f z Q z  •m的取值可以 比函数极点的 实际级数高， 而并不会影响 规则 II 的有效 性,有时候将 m 取的比实际级 数高可以简化 留数计算 0 0 0 ( ) Re [ ( ), ] '( ) P z sf z z Q z 

Review 无穷远点留数e/e以小2知手t=-c2n手.e出 ·若函数f()在扩充复平面内只有有限个孤立奇点，则f ()在所有奇点（包括0点)的留数总和必为零 Rule IV:Res[fe,o]=-Resf白)三，0] 采用留数来求解定积分有两点须满足： ·被积函数必须与某解析函数密切相关 ·积分路径是闭曲线 典型定积分留数求解 ·积分类型1：心 R(cos0,sine)de 2xi>Reslf(=).=,] k= ·R(cos0,sin0)为cos0与sin0的有理函数 lexu@mail.xidian.edu.cn F&C

lexu@mail.xidian.edu.cn F & C 3 Review 无穷远点留数  若函数f (z)在扩充复平面内只有有限个孤立奇点，则 f (z)在所有奇点（包括∞点）的留数总和必为零  Rule IV： 采用留数来求解定积分有两点须满足：  被积函数必须与某解析函数密切相关  积分路径是闭曲线 典型定积分留数求解  积分类型 I ： • R (cosθ，sinθ)为 cosθ与 sinθ的有理函数 1 1 1 Re [ ( ), ] ( ) ( ) 2 2 C C s f z f z dz c f z dz i i            2 1 1 Re [ ( ), ] Re [ ( ) ,0] sf z sf z z    2 0 R d (cos ,sin )      1 2 Re [ ( ), ] n k k i sf z z  

第21讲留数在积分中的应用及复习 冬留数在定积分中的应用( 冬复变函数复习 lexu@mail.xidian.edu.cn F&C

lexu@mail.xidian.edu.cn F & C 4 第21讲 留数在积分中的应用及复习 留数在定积分中的应用(II) 复变函数复习

留数在定积分中的应用 (II) 冬积分类型Ⅱ： "R(x)dx ·Rx)是x的有理函数 ■分母的次数至少比分子的次数高二次 ·Rc)在实轴上没有孤立奇点 ■不失一般性，设： R(z)= 2+a2-++a,m-n≥2 2"+b,2m-+…+bn lexu@mail.xidian.edu.cn F&C

lexu@mail.xidian.edu.cn F & C 5 留数在定积分中的应用（II） 积分类型 II：  R(x)是x的有理函数  分母的次数至少比分子的次数高二次  R(x)在实轴上没有孤立奇点  不失一般性，设： R x dx ( )   1 1 1 1 () , 2 n n n m m m z az a Rz m n z bz b           

留数在定积分中的应用（Ⅱ） R(z）= z”+az"+…+a -,m-n≥2 zm+bzm-+…+b 。2 C为以原点为圆心，R为半径的上半平面半圆周 ”R足够大，使得C包含上半平面所有极点z R(z)d=2πi∑Res[f(z),zk] lexu@mail.xidian.edu.cn F&C 6

lexu@mail.xidian.edu.cn F & C 6 留数在定积分中的应用（II）  CR为以原点为圆心，R为半径的上半平面半圆周  R足够大，使得CR包含上半平面所有极点zk 1 1 1 1 () , 2 n n n m m m z az a Rz m n z bz b            y x z1 z2 zk CR ( ) ( ) 2 Re [ ( ), ] R R k R C R x dx R z dz i s f z z      

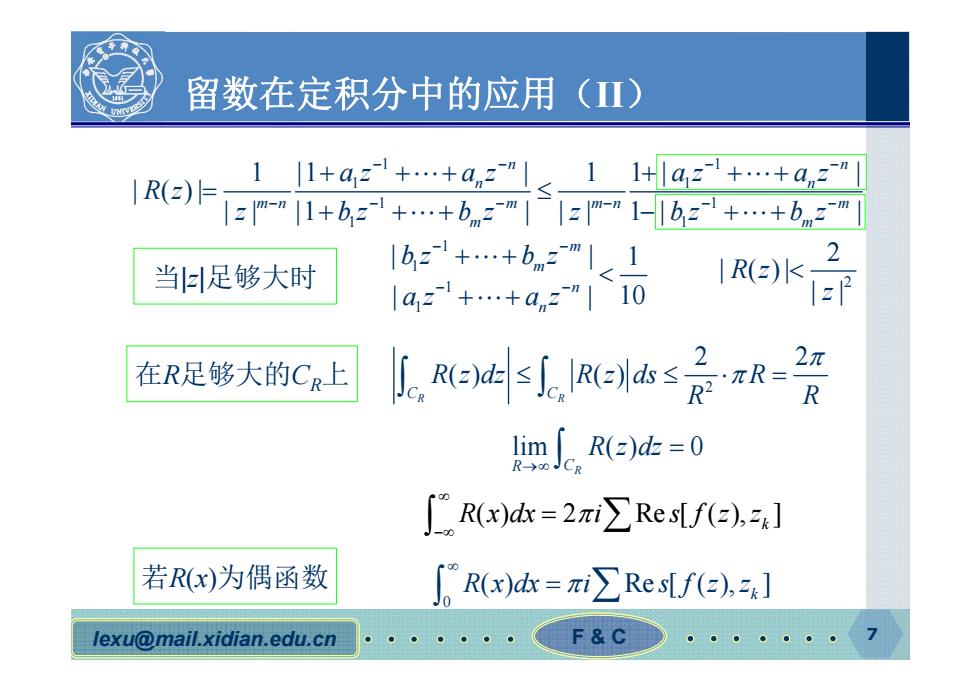
留数在定积分中的应用（Ⅱ） R( 11+a2+…+an2"1l+laz+…+a2 zm-"11+bz1+…+bnzm|1zm-"1-1bz1+…+bn2m 2 当足够大时 1bz+…+bn2m11 R()k- 1az+…+a,z"|10 在R足够大的CR上 机edRe杰≤是R- R mJ。R(e)d=0 R(x)dk=2πi∑ResLf(=,)zJ 若R(x)为偶函数 ∫Rx)k=πi∑Refe),] lexu@mail.xidian.edu.cn F&C

lexu@mail.xidian.edu.cn F & C 7 留数在定积分中的应用（II） 1 1 1 1 1 1 1 1 1 1 |1 | 1 | | | ( )| || |1 | || 1 | | n n n n mn m mn m m m az az az az R z z bz b z z bz b z                      1 1 1 1 | | 1 | | 10 m m n n bz b z az az            当|z|足够大时 2 2 | ( )| | | R z z  在R足够大的CR上 2 2 2 () () C C R R R z dz R z ds R R R      lim ( ) 0 R CR R z dz    ( ) 2 Re [ ( ), ] R x dx i s f z z  k      0 ( ) Re [ ( ), ] R x dx i s f z z  k  若R(x)为偶函数   

留数在定积分中的应用 (Ⅱ) 例1计算积分：I=二+X+ba>0,b>0 x'dx ·[解1易验证： a b ·积分函数是x的有理函数I=2πi 2i(a2-b2)2ib2-a2) ·t=4,n=2,m-=2 ·函数的奇点为士ai,士bi,不在实轴上 、 a+b ·利用积分类型Ⅱ采用留数求解，显然，在上半平面仅有 一级极点i,bi,且它们的留数为： ReR().a 2i(a2-b2) -b2 Res[R()im[()R()=2bi() lexu@mail.xidian.edu.cn F&C 8

lexu@mail.xidian.edu.cn F & C 8 留数在定积分中的应用（II） 例1 计算积分：  [解]易验证： • 积分函数是x的有理函数 • m=4，n=2，m-n=2 • 函数的奇点为±ai，±bi，不在实轴上  利用积分类型II采用留数求解，显然，在上半平面仅有 一级极点ai,bi，且它们的留数为： 2 2 22 2 ( 0, 0) ( )( ) x dx I ab x axb          2 22 22 Re [ ( ), ] lim ( ) ( ) 2 ( ) 2( ) z ai a a s R z ai z ai R z  ai b a i a b         2 22 22 Re [ ( ), ] lim ( ) ( ) 2 ( ) 2( ) z ai b b s R z bi z bi R z  bi a b i b a       22 22 2 2( ) 2( ) a b I i ia b ib a a b              

留数在定积分中的应用（Ⅱ） 冬积分类型Ⅱ： Rx)emd(a>0) ·R(x)是x的有理函数 ■分母的次数至少比分子的次数高一次 ■在实轴上没有孤立奇点 ·同样，不失一般性，设 R(z)= 2”+a2++a,m-n2l z"+b2m-1+…+bn lexu@mail.xidian.edu.cn ●●●● F&C

lexu@mail.xidian.edu.cn F & C 9 留数在定积分中的应用（II） 积分类型 III：  R(x)是x的有理函数  分母的次数至少比分子的次数高一次  在实轴上没有孤立奇点  同样，不失一般性，设 ( ) ( 0) aix R x e dx a     1 1 1 1 () , 1 n n n m m m z az a Rz m n z bz b           

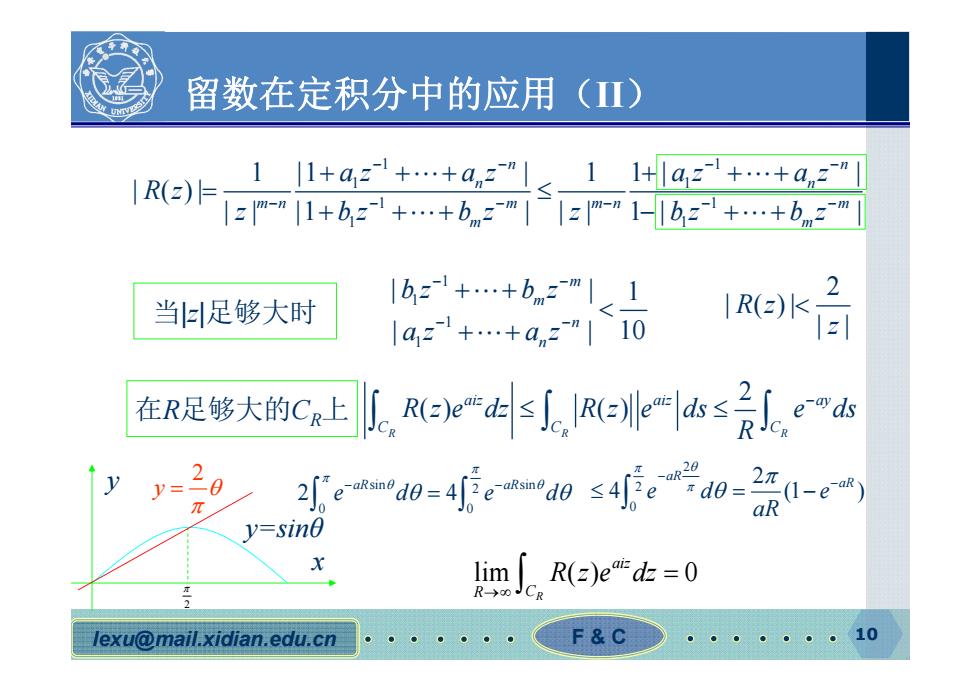
留数在定积分中的应用（Ⅱ） 1R(z)月 1_1+a2+…+a,2"11+la2+…+a,2 |zm-"11+bz+…+bnzm1|zm-"1-1bz+…+bnm2m 当足够大时 6++bl< 1a21+…+a,2"110 IRK 2 在R足够大的C。上Ree“s,Rele本≤是Leh y=20 2ed0=4e0s4ed0-2l-e) v=sin inR(E)e"d0 lexu@mail.xidian.edu.cn F&C ··10

lexu@mail.xidian.edu.cn F & C 10 留数在定积分中的应用（II） 1 1 1 1 1 1 1 1 1 1 |1 | 1 | | | ( )| || |1 | || 1 | | n n n n mn m mn m m m az az az az R z z bz b z z bz b z                      1 1 1 1 | | 1 | | 10 m m n n bz b z az az            当|z|足够大时 2 | ( )| | | R z z  在R足够大的CR上 2 () () RR R aiz aiz ay CC C R z e dz R z e ds e ds R      lim ( ) 0 R aiz R C R z e dz    sin sin 2 0 0 2 4 aR aR ed ed            x y 2  y=sinθ 2 y    2 2 0 2 4 (1 ) aR aR ed e aR         