
场论与复变函数 主讲:徐乐 2017年12月14日星期四
2017年12月14日星期四 场论与复变函数 主讲:徐乐

Review 双边幂级数 2c-”+26 ■在圆环域内收敛,且在收敛圆环域内其和函数 解析,可以逐项求导和逐项积分 洛朗级数阳-立ce-6a f(5) ·在圆环域内处处解析的函数必能展成洛朗级数 DNotel:z为洛朗级数一般项奇点,但不一定是函数fz)奇点; DNot2:给定复平面内一点z,则在以z为中心的 C3一个解析环域内洛朗展开式是唯一 (3不同解析环域内洛朗展开不唯一 DNote3:洛朗展开式的收敛园环域的圆周上必有fz)的奇点 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 2 Review 双边幂级数 在圆环域内收敛,且在收敛圆环域内其和函数 解析,可以逐项求导和逐项积分 洛朗级数 在圆环域 内处处解析的函数必能展成洛朗级数 Note1:z0为洛朗级数一般项奇点,但不一定是函数f(z)奇点; Note2:给定复平面内一点z0 ,则 在以z0为中心的 一个解析环域内洛朗展开式是唯一 不同解析环域内洛朗展开不唯一 Note3:洛朗展开式的收敛园环域的圆周上必有f(z) 的奇点 1 0 n nn n nn nn n cz c z cz 0 () ( )n n n f z cz z 1 0 1 () 2() n n C f c d i z

Review ·洛朗级数与泰勒级数 在圆域z-zKR内解析的函数可在z展开成泰 勒级数 ·在圆环域R<k-zKR2内解析的函数可在z展 开成洛朗级数 o若函数在z-z<R2内解析,则洛朗级数变成泰勒级 数,即泰勒级数是洛朗级数的特殊形式 2πi ∮f5)(5-)d5=0 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 3 Review 洛朗级数与泰勒级数 在圆域 |z-z0|< R 内解析的函数可在z0展开成泰 勒级数 在圆环域 R1<|z-z0|< R2 内解析的函数可在z0展 开成洛朗级数 若函数在|z-z0|< R2内解析,则洛朗级数变成泰勒级 数,即泰勒级数是洛朗级数的特殊形式 1 1 0 1 () 0 2 n n K c f zd i

Review 。洛朗级数展开的方法: ■直接法:通过定义求解 ■间接法:通过间接方法展开 洛朗级数的应用: ·若C为圆环域R,<zz<R2内的任意一条简单 闭曲线,且fz)在圆环域内解析 ∮f(5)d5=2πic, lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 4 Review 洛朗级数展开的方法: 直接法:通过定义求解 间接法:通过间接方法展开 洛朗级数的应用: 若C为圆环域 R1 < |z-z0|<R2 内的任意一条简单 闭曲线,且f(z)在圆环域内解析 1 () 2 C f d ic
第19讲 留数基础 必孤立奇点 ·可去奇点 极点 ·本性奇点 冬零点 函数的零点与极点 函数在无穷远点的性态 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 5 第19讲 留数基础 孤立奇点 可去奇点 极点 本性奇点 零点 函数的零点与极点 函数在无穷远点的性态
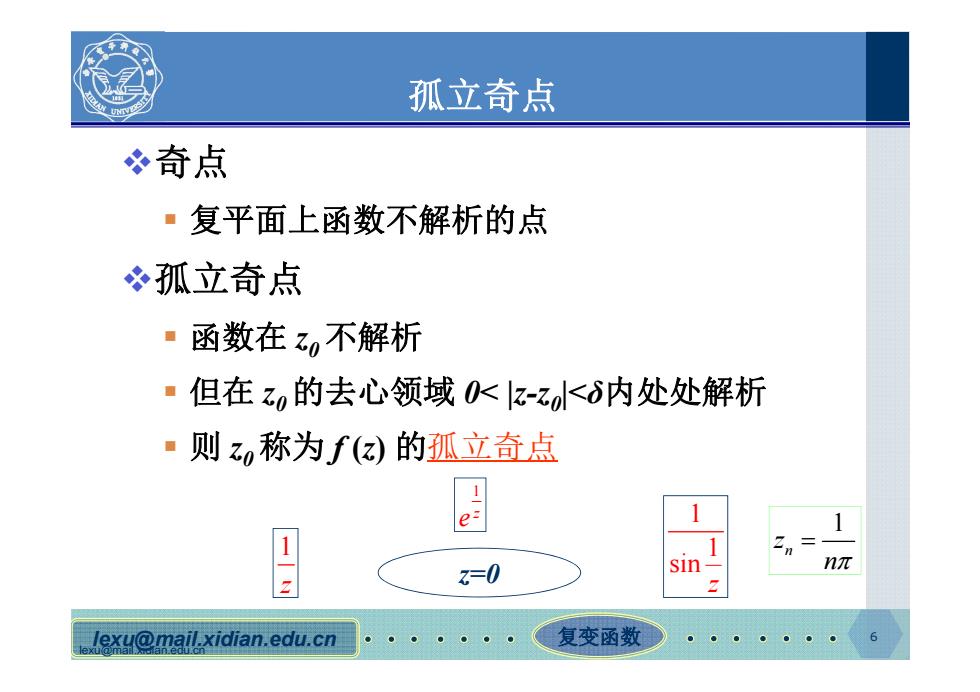
孤立奇点 奇点 ·复平面上函数不解析的点 冬孤立奇点 ·函数在z,不解析 ▣但在z的去心领域0<z-z<δ内处处解析 ·则zn称为f(z)的孤立奇点 e 1- z=0 nπ lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 6 孤立奇点 奇点 复平面上函数不解析的点 孤立奇点 函数在 z0 不解析 但在 z0 的去心领域 0< |z-z0|<δ内处处解析 则 z0 称为 f (z) 的孤立奇点 1 z 1 z e 1 1 sin z z=0 1 n z n

孤立奇点 ·由洛朗级数展开性质可知,函数在其孤立 奇点的去心领域内必可展开成洛朗级数 根据洛朗展开式的不同特点,可将孤立奇 点分为三类: ·可去奇点 ·极点 ■本性奇点 lexu@mail.xidian.edu.cn 复变函数●
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 7 孤立奇点 由洛朗级数展开性质可知,函数在其孤立 奇点的去心领域内必可展开成洛朗级数 根据洛朗展开式的不同特点,可将孤立奇 点分为三类: 可去奇点 极点 本性奇点
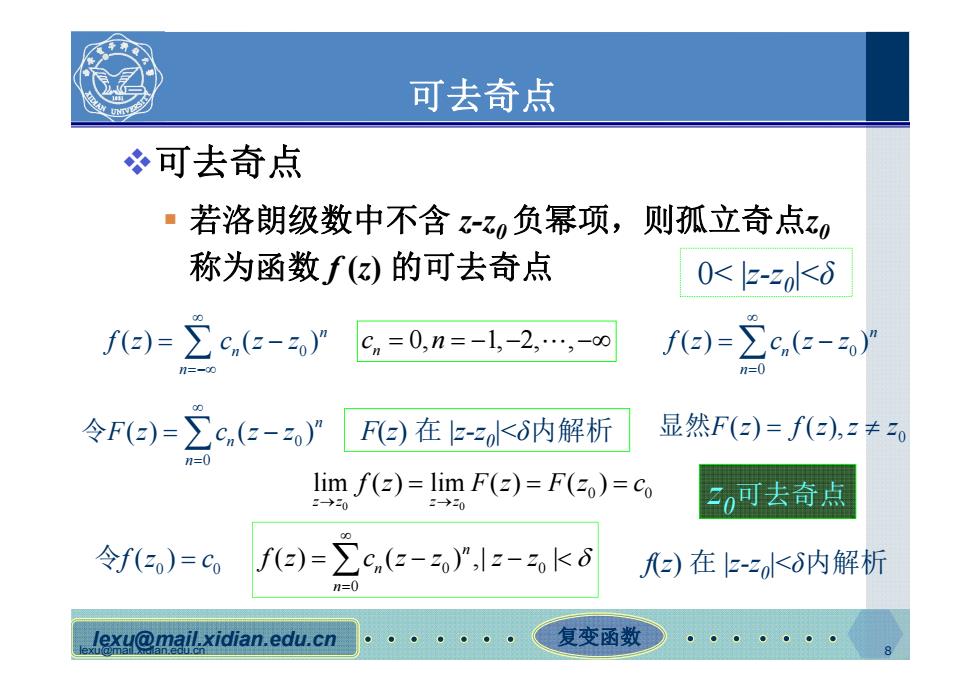
可去奇点 必可去奇点 ·若洛朗级数中不含z-z负幂项,则孤立奇点z0 称为函数f()的可去奇点 0<2-zKδ fe)=∑c,e- cn=0,n=-1,-2,…,-∞ f()-Ec.(--3 令F-c6- Fz)在-z<6内解析 显然F(z)=f(z),z≠o lim f(z)=lim F()=F(zo)=co 2→2 0可去奇点 令f(z)=c fa)=∑c(2-2),lz-2okd z)在-z<δ内解析 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 8 可去奇点 可去奇点 若洛朗级数中不含 z-z0 负幂项,则孤立奇点z0 称为函数 f (z) 的可去奇点 0 () ( )n n n f z cz z 0, 1, 2, , n c n 0 0 () ( )n n n f z cz z 0< |z-z0|<δ 0 0 () ( )n n n F z cz z 令 F(z) 在 |z-z0|<δ内解析 0 显然F( ) ( ), z fz z z 0 0 0 0 lim ( ) lim ( ) ( ) zz zz f z Fz Fz c 0 0 令f ( ) z c 0 0 0 ( ) ( ) ,| | n n n fz c z z z z f(z) 在 |z-z0|<δ内解析 z0可去奇点

可去奇点 冬例1验证=0是 可去奇点,并讨论函数在 可去奇点处的性质 [解]显然,函数仅在z=0处不解析,在除去此点的 复平面上解析,因此,=0是函数的孤立奇点 求解函数的洛朗级数可得: +1 511 51 ·洛朗展开无负幂项,即该点为函数的可去奇点 ·显然,若令函数在z=0处的值为1,则函数在z=0处解析 C0=1 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 9 可去奇点 例1 验证 z=0是 可去奇点,并讨论函数在 可去奇点处的性质 [解] 显然,函数仅在z=0处不解析,在除去此点的 复平面上解析,因此, z=0是函数的孤立奇点 求解函数的洛朗级数可得: 洛朗展开无负幂项,即该点为函数的可去奇点 显然,若令函数在z=0处的值为1,则函数在z=0处解析 sin z z sin 1 1 1 1 1 35 24 ( )1 3! 5! 3! 5! z zz z z z z z c0=1

极点 冬极点 ·若洛朗级数的z-z,负幂项仅有有限个,且最高 负幂项为(z-乙)m,则孤立奇点z称为函数 fa)的m级极点,即 fa)=c(-)”+∑c,(e-广,m≥l,c.0 D具有m级极点的函数也可写成如下形式: fe)= 1 g(e)在-z<δ内解析 (8() 8(20)0 8(2)=C-m+C-m1(2-20)+C-m+2(2-)2…+… lexy@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn lexu@mail.xidian.edu.cn 复变函数 10 极点 极点 若洛朗级数的 z-z0 负幂项仅有有限个,且最高 负幂项为 ( z - z0 )m ,则孤立奇点 z0 称为函数 f (z) 的m级极点,即 具有m级极点的函数也可写成如下形式: 0 0 1 1 ( ) ( ) ( ) , 1, 0 m n n nn m n n fz c z z c z z m c 0 1 () () ( )m f z g z z z 2 10 20 () ( ) ( ) mm m gz c c z z c z z g(z) 在 |z-z0|<δ内解析 g(z0) ≠0