
西安电子科枝大学 电子工程学院《D School of Electronic Engineering.Xidian University http://see .xidian.edu.cn n.edu.ch 场论与复变函数 xuamail.x 主讲:徐乐 2011年11月6日星期日
lexu@mail.xidian.edu.cn

Review lexuamail.xidian.edu.cx ■复变函数积分 。积分的定义 ·积分存在的条件 积分的性质 ■柯西古萨基本定理 闭路变形定理 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

复变函数的积分 ■复变函数积分的定义: ·设函数f2定义在区域D内 ·C为D内始于A终于B的光滑有向曲线 ·将曲线C任意分为n个弧段,其分点为: ■A=2021,22,…41,B ·在每个弧段到z上任取一点 。当无限增加,且δ趋于零时,若不论对C的分法及g的 取法如何,S有唯一极限,则该极限称为函数沿曲 线C的积分,记作: ∫cfa正-m∑f5)△ lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

积分存在的条件及计算方法 「fet=jk-d+et*d ·Note1:当复变函数fe连续,曲线C光滑时,积分Jfz)d 定存在 Note2: ∫f()b可通过两个三元实变函数线积分来计算 ■Note3: 若C是由C,C2.,C等光滑曲线按段依次互 连构成的按段光滑曲线,则 f()df(2)d+f(a)d++f(z)d ■Note4:对于沿参数形式描述曲线的复变函数积分 fa)k=九y0d lexu@mail.xidian.edu.cn 若无特殊声明,总假定被积函数连续且曲线按段光滑
lexu@mail.xidian.edu.cn

复变函数的积分 复变函数积分的性质 edu. ·设a及g)在简单曲线C上连续,则有 ·(四财a)d=afat,其中a是个复常数: ·(2) If(=)+g()K--[f(=)d+g(d ·3) fad=fad±Lfed++Lfe)延 ·(4④) Jdfe)d=-fed° 若C是简单闭曲线,可取C上任一点作为积分起点,且当沿C取积分的 方向改变时所得积分相应变号。 ·(S)如果在C上,f<M,而L是曲线C的长度,其中M及L都是有 限的正数,那么有fe)止KM lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn
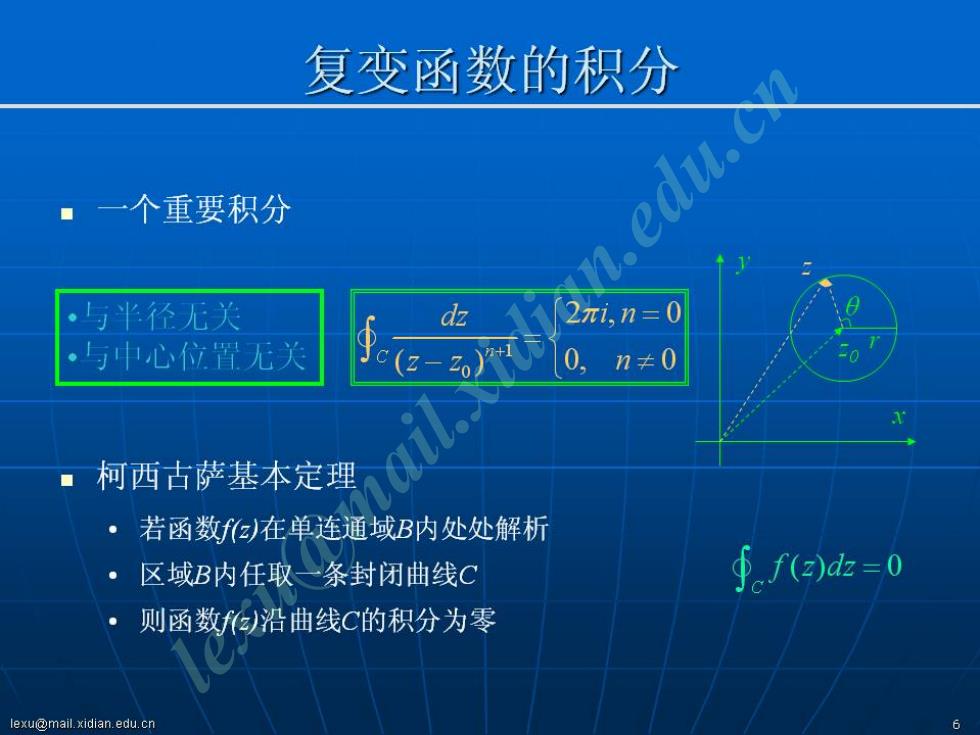
复变函数的积分 一个重要积分 n edu. 。与半径无关 dz 2元i,n=0 。与申心位置无关 Jc(z-20) 0,n≠0 ■柯西古萨基本定理 ·若函数f在单连通域B内处处解析 。 区域B内任取条封闭曲线C ∮.fe)dk=0 。 则函数)沿曲线C的积分为零 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

柯西-古萨定理 ■柯西-古萨基本定理 edu. ·若函数f)在单连通域B内处处解析 ·区域B内任取一条封闭曲线C ·则函数f沿曲线C的积分为零 exuamal lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

闭路变形定理 ■柯西-古萨定理只能适用于单连通域 ■对于多连通域 ·松)在多连通域内解析 ·假设C与C,为D内的任意两条简单闭曲线 ·正向为逆时针方向 ■C在C的内部 ·以C,及C为边界的区域D全含于D ·将两条简单闭曲线C及C,看成一条复合闭路 ∮/edk=0 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

闭路变形定理 ■闭路变形定理 ·一个解析函数沿闭曲线的积分,不因闭曲线在区域内 作连续变形而改变它的值,只要在变形过程中曲线不 经过函数f不解析点 ■复合闭路定理 ·设C为多连通域D内的一条简单闭曲线 ·C1C2,,Cn是在C内部的简单闭曲线 ■它们互不包含也互不相交 ▣以C,C2,C为边界的区域全包含于I ·fz在D内解析 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

第13讲复变函数积分() lexuamail.xidian.edu. ■原函数与不定积分 ■柯西积分公式 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn